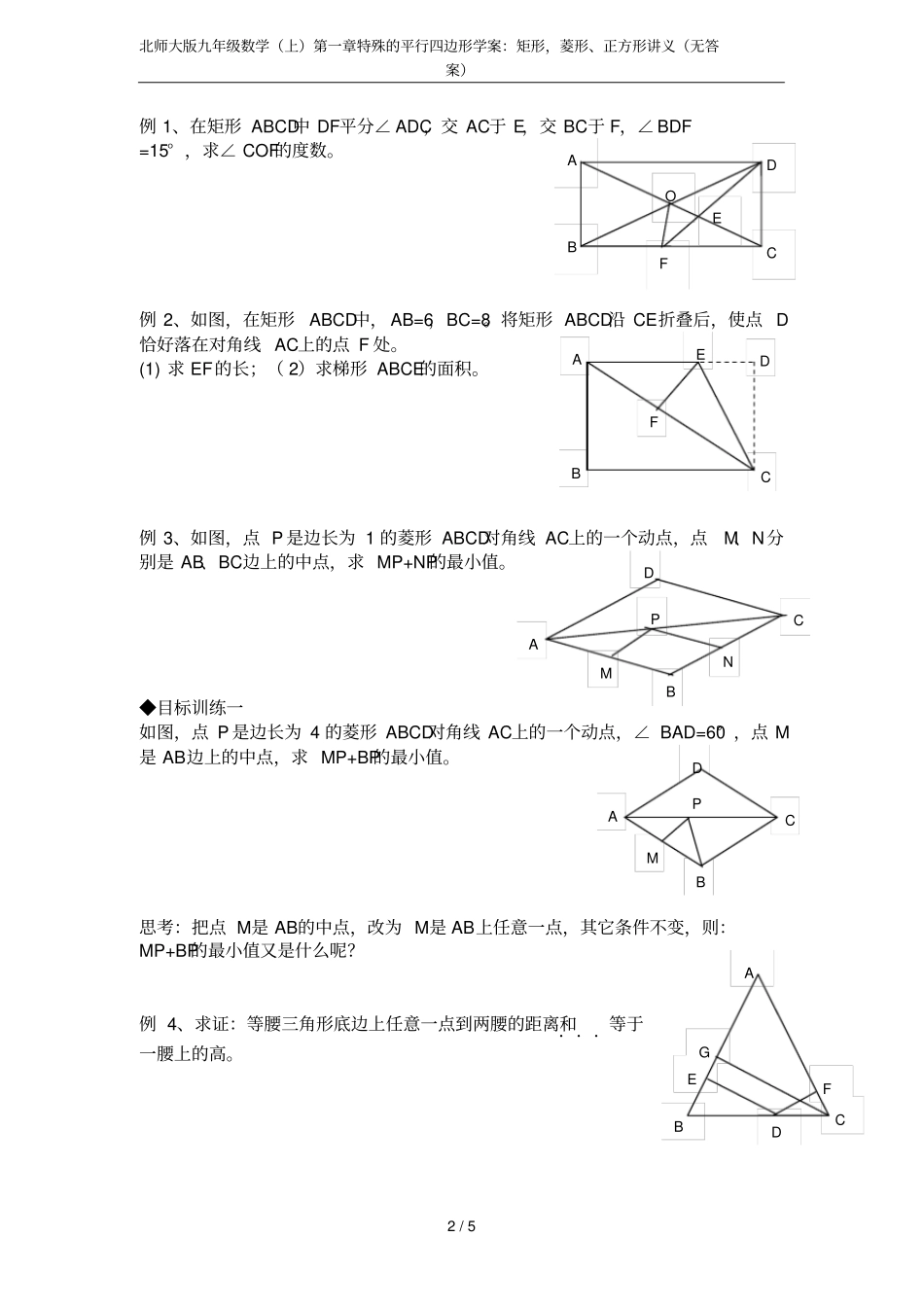
北师大版九年级数学(上)第一章特殊的平行四边形学案:矩形,菱形、正方形讲义(无答案)1/5矩形、菱形、正方形讲义【基础知识概述】(一)〖知识框架〗(二)〖几种特殊四边形的性质〗边角对角线平行四边形对边平行且相等对角相等两条对角线互相平分矩形对边平行且相等四个角都是直角两条对角线互相平分且相等菱形对边平行四边相等对角相等两条对角线互相垂直平分,每条对角线平分一组对角正方形对边平行四边相等四个角都是直角两条对角线互相垂直平分且相等,每条对角线平分一组对角(三)〖几种特殊四边形的常用判定方法〗平行四边形(1)两组对边分别平行;(2)两组对边分别相等;(3)一组对边平行且相等;(4)两条对角线互相平分;(5)两组对角分别相等。矩形(1)有三个是直角;(2)是平行四边形且有一个角是直角;(3)是平行四边形且两条对角线相等。菱形(1)四条边都相等;(2)是平行四边形且有一组邻边相等;(3)是平行四边形且两条对角线互相垂直。正方形(1)是矩形,且有一组邻边相等;(2)是菱形,且有一个角是直角。(四)〖几个重要结论〗1.两平行线间的距离处处相等.2.同底(等底)同高(等高)的三角形面积相等.3.同底(等底)同高(等高)的平行四边形面积相等.4.菱形的面积等于两对角线乘积的一半.5.直角三角形斜边上的中线等于斜边的一半.6.直角三角形中,如果有一个锐角等于30°,那么30°所对的直角边等于斜边的一半.【典型例题解析】北师大版九年级数学(上)第一章特殊的平行四边形学案:矩形,菱形、正方形讲义(无答案)2/5例1、在矩形ABCD中DF平分∠ADC,交AC于E,交BC于F,∠BDF=15°,求∠COF的度数。例2、如图,在矩形ABCD中,AB=6,BC=8。将矩形ABCD沿CE折叠后,使点D恰好落在对角线AC上的点F处。(1)求EF的长;(2)求梯形ABCE的面积。例3、如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M、N分别是AB、BC边上的中点,求MP+NP的最小值。◆目标训练一如图,点P是边长为4的菱形ABCD对角线AC上的一个动点,∠BAD=60°,点M是AB边上的中点,求MP+BP的最小值。思考:把点M是AB的中点,改为M是AB上任意一点,其它条件不变,则:MP+BP的最小值又是什么呢?例4、求证:等腰三角形底边上任意一点到两腰的距离和...等于一腰上的高。FEOBACDBDAFECMCBADNPPMCADBBEDGACF北师大版九年级数学(上)第一章特殊的平行四边形学案:矩形,菱形、正方形讲义(无答案)3/5◆目标训练二1、求证:等腰三角形底边延长线上任意一点到两腰的距离差...等于一腰上的高。2、在矩形ABCD中,AB=4,AD=3,P为AB上的动点,PE⊥AC于E,PF⊥BD于F,求:PE+PC的值。.【创新中考思维训练】例5、(1)、如图,矩形ABCD中,点E、F分别是AB、CD的中点,连接DE和BF,分别取DE、BF的中点M、N,连接AM,CN,MN,若AB=22,BC=23,则图中阴影部分的面积为.(2)、如图:ABCD是正方形,E是CF上的一点,若DBEF是菱形,则EBC()A、15B、5.22C、30D、25(3)、如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上.下列结论:①、CE=CF;②、∠AEB=75°;③、BE+DF=EF;④、32ABCDS正方形.其中正确的序号是.(把你认为正确的都填上)例6、如图:D是等腰直角三角形ABC的直角边BC上一点,AD的垂直平分线EF分别交AC、AD、AB于E、M、F,2BC。(1)当2CD时,求AE的长;(2)当AD平分BAC时,四边形AEDF是何种特殊的平行四边形?请证明你的结论,并求出CD的长;例7、(1)线段AB上任取一点C,分别以AC和BC为边作等边三角形,试回答ACEDFCBGEAOADCBEFpABCDEF北师大版九年级数学(上)第一章特殊的平行四边形学案:矩形,菱形、正方形讲义(无答案)4/5可看作哪个三角形怎么样旋转得到。(不用说明理由)(2)线段AB上任取一点C,分别以AC和BC为边作正方形,连接DG,M为DG中点,连接EM并延长交FG于N,连接FM,猜测FM和EM的关系,并说明理由。(3)在(2)的基础上将正方形CBGF绕C点旋转,其它条件不变,猜测FM和EM的关系,并说明理由。◆目标训练三1、如图,在直线a上依次摆放着七个正方形,已知斜放的三个正方形的面积分别为1、2、3。则____________4321ss...