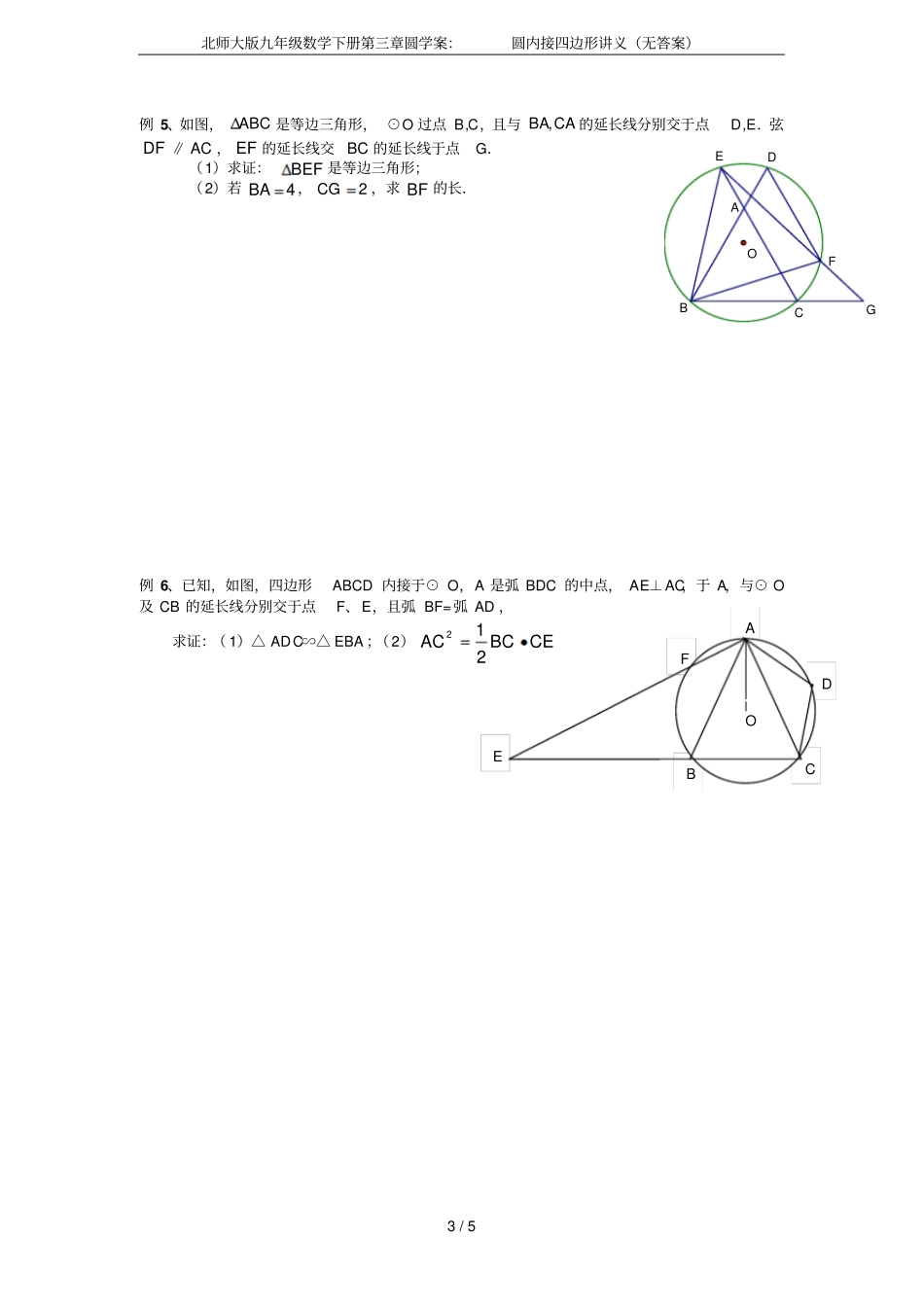
北师大版九年级数学下册第三章圆学案:圆内接四边形讲义(无答案)1/5圆心角、圆周角、圆内接四边形讲义【基础知识精讲】一、圆心角:1.圆心角:顶点在圆心,两边和圆相交的角叫做圆心角。2.圆心角的度数等于它所夹弧的度数二、圆周角:1、圆周角:顶点在圆上,它的两边和圆还有另一个交点的角叫做圆周角。2、圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半。推论1:在同圆或等圆中,同弧或等弧所对的圆周角相等。推论2:半圆或直径所对的圆周角是直角。90°的圆周角所对的弦是直径。推论3:圆的两条平行弦所夹的弧相等。3、弧的度数:一段弧的度数等于它所对的圆心角的度数。4、圆外角的度数等于它所夹的两段弧的度数的差的一半。5、圆内角的度数等于它所对的两段弧的度数的和的一半。6直径所对的圆周角是直角;圆周角是直角,它所对的弦是直径。三、圆的有关性质:1.圆的确定:(1).圆心确定圆的位置半径确定圆的大小。(2).不在同一直线上的三个点确定一个圆。(3).三角形的三个顶点确定一个圆,这个圆叫做三角形的外接圆,外接圆的圆心是三角形三边垂直平分线的交点,叫做三角形的外心。(4)锐角三角形的外心在三角形的内部,钝角三角形的外心在三角形的外部,直角三角形的外心在斜边中点。2.圆的对称性:(1).圆是轴对称图形,任何一条经过圆心的直线都是它的对称轴。(2)圆是中心对称图形,圆心是它的对称中心。说明:一个圆的对称轴有无数条,对称中心只有一个,一个圆绕圆心旋转任意角度,都能够和原图形重合,即圆还具有旋转不变性。四、在解决圆的有关问题时,有以下几种常引用的辅助线:(1)连弦的端点与圆心的半径;(2)作弦心距;(3)连圆心和弦的中点(遇弦的中点时);(4)连圆心和弧的中点(遇弧的中点时);(5)作半圆上的圆周角。五、圆的内接四边形的性质:(1)圆的内接四边形对角互补。(2)推论:圆的内接四边形的一个外角等于它的内对角。【重难点高效突破】例1、如图,OA,OB,OC,都是圆的半径,∠AOB=2∠BOC,求证:∠ACB=2∠BAC。CBAO北师大版九年级数学下册第三章圆学案:圆内接四边形讲义(无答案)2/5例2、如图,MN是⊙O直径,MN=2,点A在⊙O上∠AMN=30°,B为弧AC的中点,P为直径MN上一动点,求PA+PB的最小值。例3、已知,如图,弧AB与弧AD的度数之差为20°,弦AB,CD交于点E,∠CEB=60°,求∠CAB的度数。例4、如图,AB是直径,AC为弦,CD⊥AB于D,若AE=AC,BE交⊙O于F,连结CF,DE,求证:(1)ABADAE2;(2)∠ACF=∠AED.DBACEFEABCDO北师大版九年级数学下册第三章圆学案:圆内接四边形讲义(无答案)3/5例5、如图,ABC是等边三角形,⊙O过点B,C,且与CABA,的延长线分别交于点D,E.弦DF∥AC,EF的延长线交BC的延长线于点G.(1)求证:BEF是等边三角形;(2)若4BA,2CG,求BF的长.例6、已知,如图,四边形ABCD内接于⊙O,A是弧BDC的中点,AE⊥AC,于A,与⊙O及CB的延长线分别交于点F、E,且弧BF=弧AD,求证:(1)△ADC∽△EBA;(2)CEBCAC212OGEBDCAFFBECDAO北师大版九年级数学下册第三章圆学案:圆内接四边形讲义(无答案)4/5【名书、名校、中考、竞赛在线】A组一、填空题或选择题:(1)已知⊙O的弦AB等于圆的半径,则弦AB所对的圆心角为____________,圆周角为________________.(2)在⊙O中,同弦所对的圆周角()A、相等B、互补C、相等或互补D、都不对(3)已知半径为5的⊙O中,弦AB=25,弦AC=5,则∠BAC=()A、15°B、210°C、105°或15°D、210°或30°(4)如图,四边形ABCD内接于⊙O,∠AOC=100°,则∠ABC=________;∠ADC=______。(5)如图,已知AB是⊙O的直径,AB=AC,BC交⊙O于D,AC交⊙O于点E,∠BAC=45°,给出以下五个结论:①∠EBC=22.5°②BD=DC③AE=2EC④劣弧AE是劣弧DE的2倍⑤AE=BC,其中正确结论的序号是_______________。(6)如图,线段AB与CD都是⊙O中的弦,其中弧AB=108°,AB=a,弧CD=36°,CD=b,则⊙O的半径R=_________________。(a-b或ab)B组已知,如图,C为半圆上一点,弧AC=弧CE,过点C?作直径AB的垂线CP,P为垂足,弦AE分别交PC,CB于点D,F.(1)求证:AD=CD;(2)若DF=54,tan∠ECB=34,求PB的长.BCDFP·OAEDCBAODECBAOBACDO北师大版九年级数学下册第三章圆学案:圆内接四边形讲义(无答案)5/5