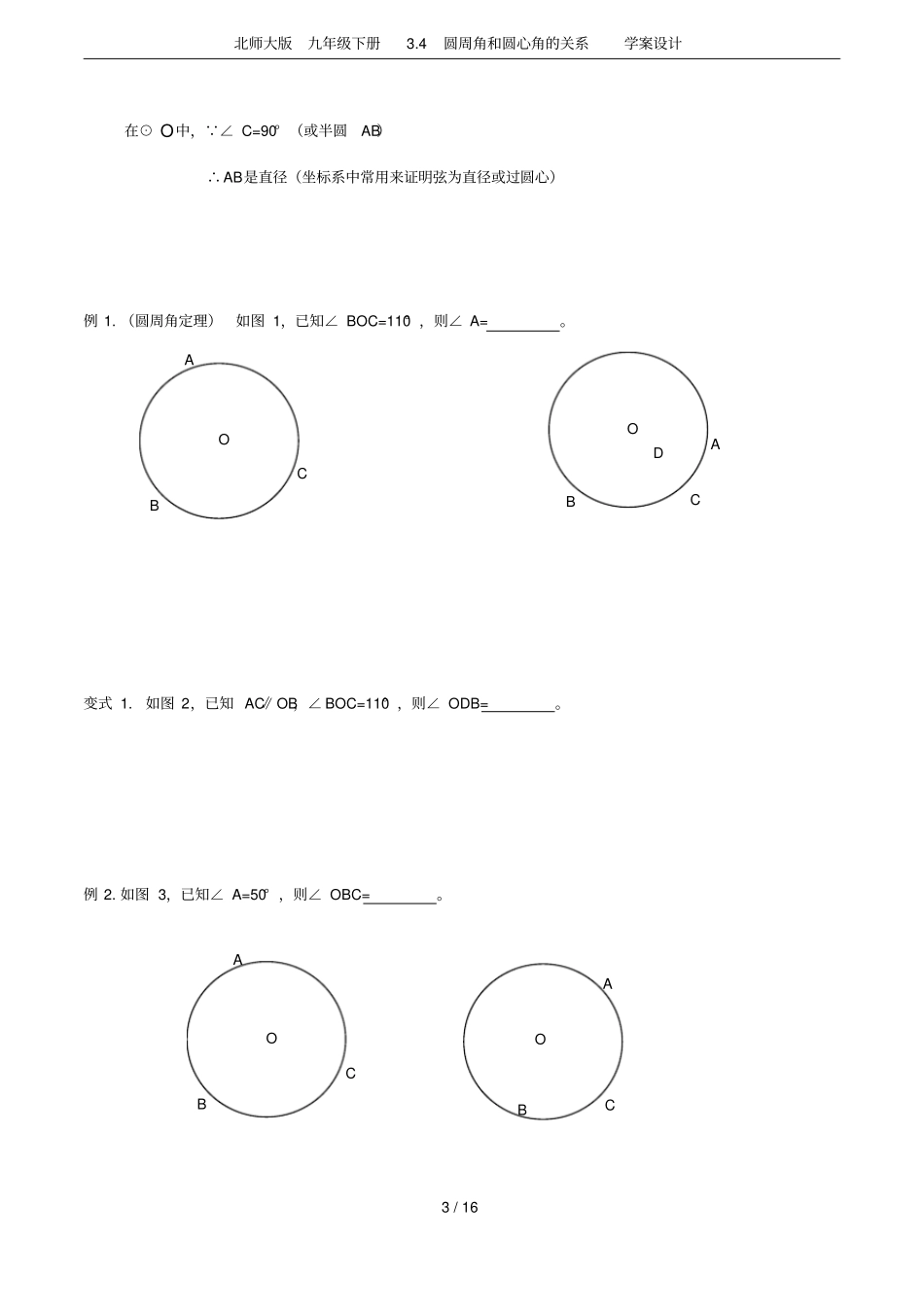
北师大版九年级下册3.4圆周角和圆心角的关系学案设计1/16圆周角与圆心角知识点一圆心角圆心角定理:在同圆或等圆中,相等的圆心角所对的弦相等,所对的弧相等,弦心距相等。如图,只要知道下列其中的1个相等,则可以推出其它的3个结论①∠AOB=∠DOE;②AB=DE;③OC=OF;④弧BA=弧BD任意弦或者弧所对的圆心角只有一个,故很多较复杂的求角度问题寻找圆心角会更简单。例1.如图,在圆O中,弦AB与弦CD相交于点P,AB=CD。(1)求证:BP=CP(2)若AB⊥CD,圆0半径为2,已知Rt△BPD的面积为2,求弦AB的值OABCDPFEDCBAO北师大版九年级下册3.4圆周角和圆心角的关系学案设计2/16知识点二圆周角圆周角定理:同弧或等弧所对的圆周角等于它所对的圆心角的一半如图,在⊙O中, ∠AOB和∠ACB分别是是弧AB所对的圆心角和圆周角∴∠AOB=2∠ACB任意弦或者弧所对的圆周角有无数个,故较麻烦的求角度转换为圆心角会更清晰。推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧是等弧。如图,在⊙O中, ∠C、∠D都是弧AB所对的圆周角∴∠C=∠D推论2:(重要)半圆或直径所对的圆周角是直角;圆周角是直角所对的弧是半圆,所对的弦是直径。(证明弦是直径)如图,在⊙O中, AB是直径(或半圆AB)∴∠C=90°CBAOCBAODCBAO北师大版九年级下册3.4圆周角和圆心角的关系学案设计3/16OABCOABC在⊙O中, ∠C=90°(或半圆AB)∴AB是直径(坐标系中常用来证明弦为直径或过圆心)例1.(圆周角定理)如图1,已知∠BOC=110°,则∠A=。变式1.如图2,已知AC∥OB,∠BOC=110°,则∠ODB=。例2.如图3,已知∠A=50°,则∠OBC=。OABCOABCD北师大版九年级下册3.4圆周角和圆心角的关系学案设计4/16OxyABCDOBCADOBCAD变式1.如图4,已知∠ACO=50°,则∠B=。例3.(直径所对圆周角为直角)如图,AB为⊙O的直径,若CA=CD,且∠ACD=40°,则∠CAB=。变式1.如图,在⊙O中,AD为直径,AB=BC,C为弧AD的中点,则∠C=。例4.如图,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A优弧上一点,则∠OBC的余弦值为。北师大版九年级下册3.4圆周角和圆心角的关系学案设计5/16DABCOCABCABDCABD变式1.如图,直径为10的⊙D中,0C=8,则∠OAC的外角的余弦值为。例5.(圆内接四边形)如图,已知∠A=85°,则∠D=。变式1.如图,已知∠AOB=110°,则∠C=。例6.如图,已知△ABC内接于圆0,以BC为底边作等腰三角形BCD,连接AD(1)当D点落在弧BC上时,求证:AD平分∠BAC(2)当D点落在优弧BC上时,求证:AD平分∠BAC的外角北师大版九年级下册3.4圆周角和圆心角的关系学案设计6/16ECABOD例7.如图AB是圆O的直径,AC=BD,BE垂直过C的直线CE。(1)求证:△ABC∽△CBE(2)图中还有其它相似吗?北师大版九年级下册3.4圆周角和圆心角的关系学案设计7/16CABDE例8.如图A、B、C、D是圆上任意四点,求证AE·DE=BE·CE变式1.如图,点A,B,C,D为⊙O上的四个点,AC平分∠BAD,AC交BD于点E,则图中有多少组相似?北师大版九年级下册3.4圆周角和圆心角的关系学案设计8/16中考真题1.(2016兰州)如图,在⊙O中,点C是的中点,∠A=50o,则∠BOC=()。(A)40o(B)45o(C)50o(D)60o2.(2016兰州)如图,四边形ABCD内接于⊙O,四边形ABCO是平行四边形,则∠ADC=()(A)45o(B)50o(C)60o(D)75o3.(2016四川自贡)如图,⊙O中,弦AB与CD交于点M,∠A=45°,∠AMD=75°,则∠B的度数是()A.15°B.25°C.30°D.75°4.(2016四川达州)如图,半径为3的⊙A经过原点O和点C(0,2),B是y轴左侧⊙A优弧上一点,则tan∠OBC为()北师大版九年级下册3.4圆周角和圆心角的关系学案设计9/16A.B.2C.D.5.(2016浙江省舟山)把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则的度数是()A.120°B.135°C.150°D.165°6.(2016广东茂名)如图,A、B、C是⊙O上的三点,∠B=75°,则∠AOC的度数是()A.150°B.140°C.130°D.120°7.(2016山东省聊城市)如图,四边形ABCD内接于⊙O,F是上一点,且=,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为()北师大...