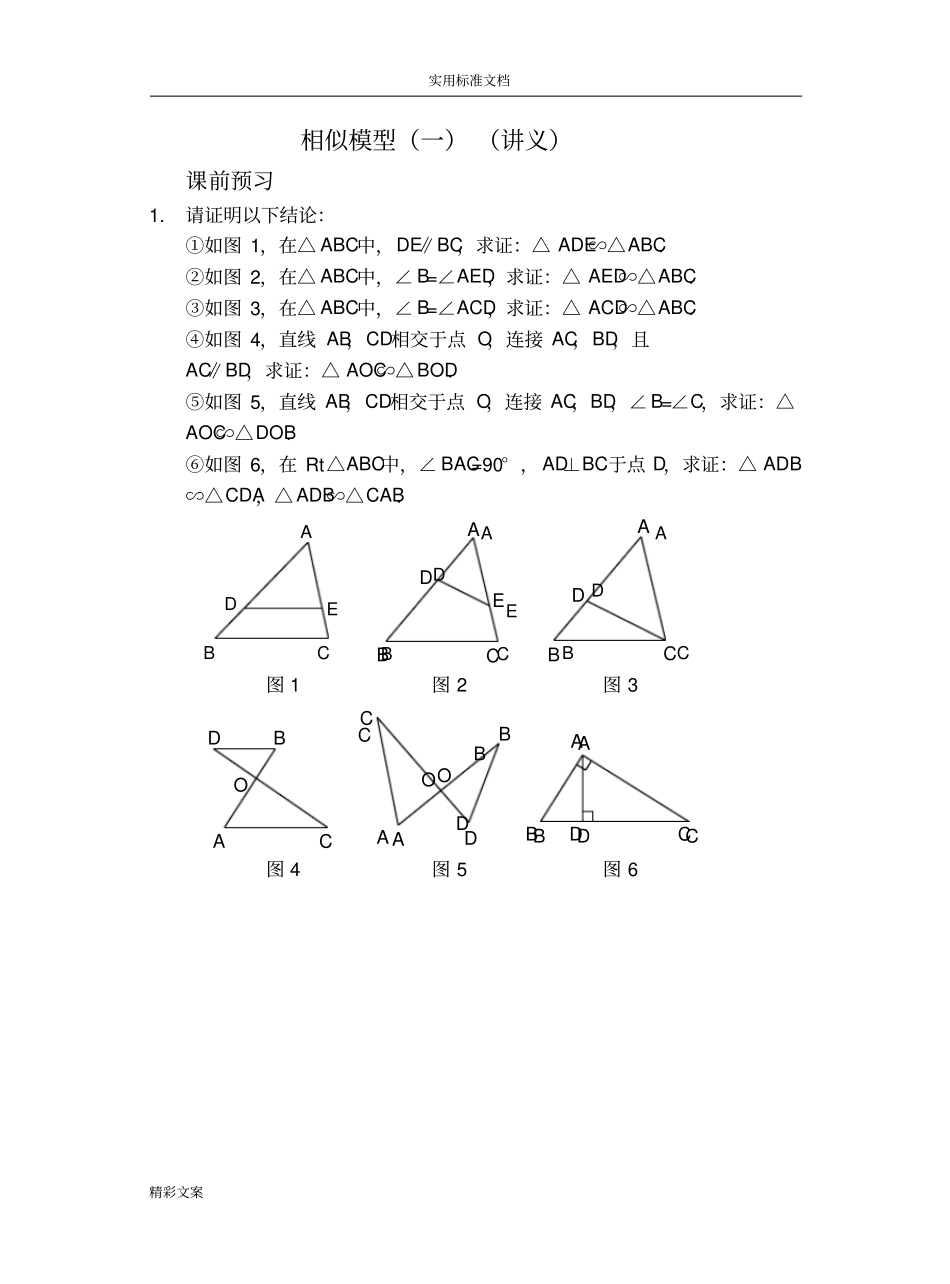
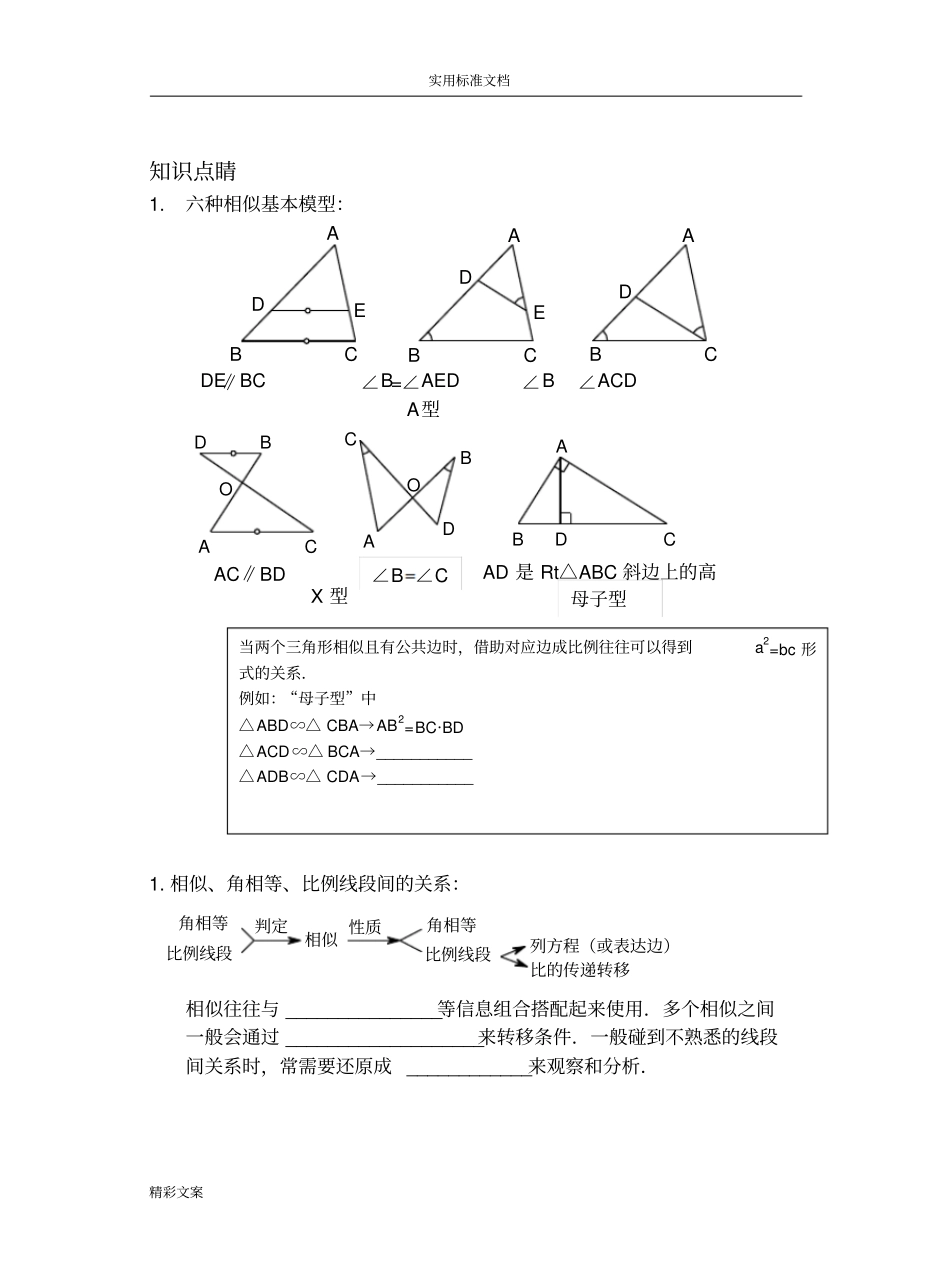
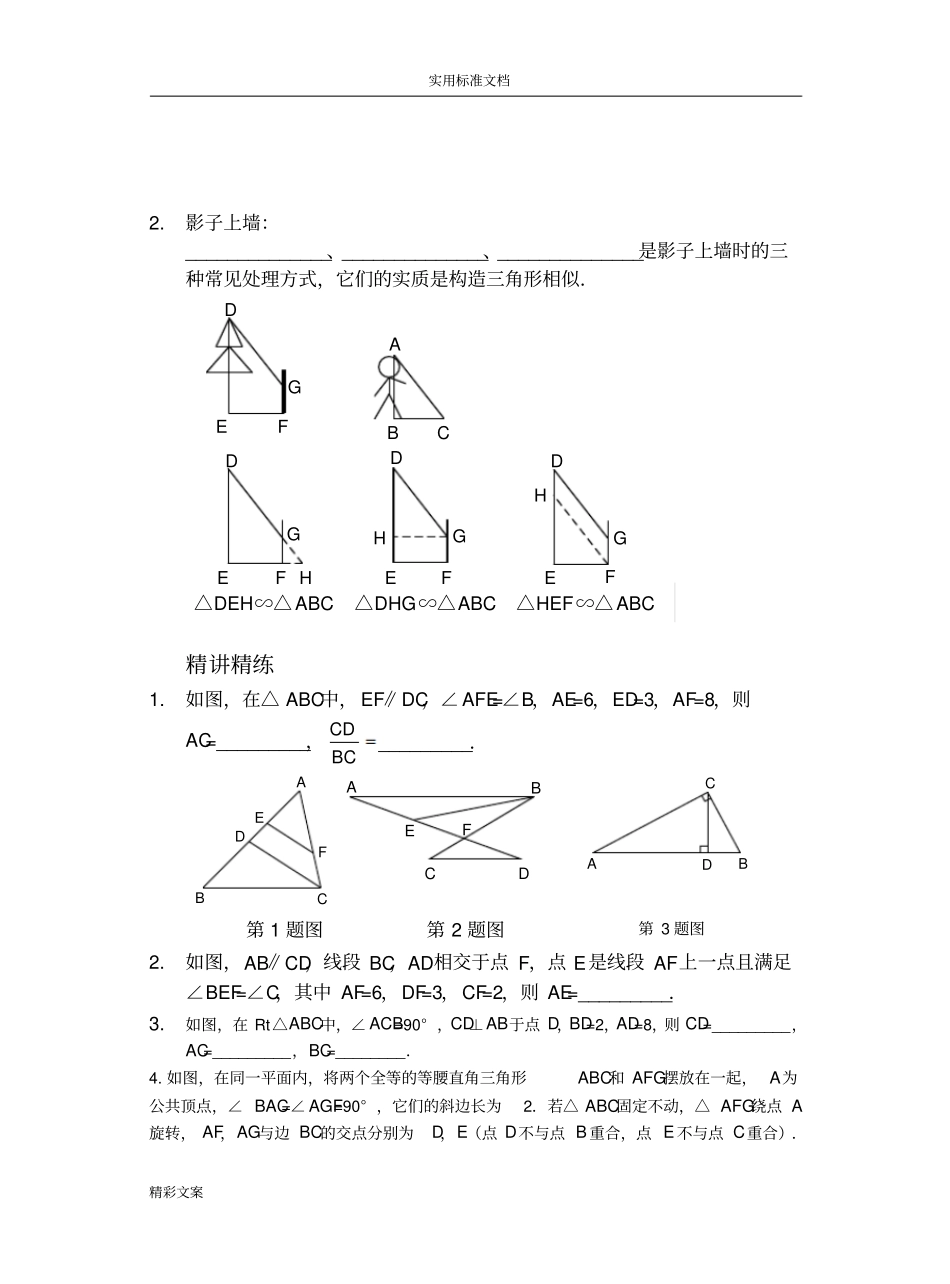
实用标准文档精彩文案相似模型(一)(讲义)课前预习1.请证明以下结论:①如图1,在△ABC中,DE∥BC,求证:△ADE∽△ABC.②如图2,在△ABC中,∠B=∠AED,求证:△AED∽△ABC.③如图3,在△ABC中,∠B=∠ACD,求证:△ACD∽△ABC.④如图4,直线AB,CD相交于点O,连接AC,BD,且AC∥BD,求证:△AOC∽△BOD.⑤如图5,直线AB,CD相交于点O,连接AC,BD,∠B=∠C,求证:△AOC∽△DOB.⑥如图6,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,求证:△ADB∽△CDA,△ADB∽△CAB.CBCBBCDEADAEDAABCDDECBA图1图2图3ADBCODBACCAODBOCDABADBC图4图5图6实用标准文档精彩文案AD是Rt△ABC斜边上的高知识点睛1.六种相似基本模型:CBCBBCDEADAEDADE∥BC∠B=∠AED∠B∠ACDA型ADBCODBACCAODB1.相似、角相等、比例线段间的关系:比的传递转移列方程(或表达边)比例线段角相等性质相似判定比例线段角相等相似往往与_______________等信息组合搭配起来使用.多个相似之间一般会通过___________________来转移条件.一般碰到不熟悉的线段间关系时,常需要还原成____________来观察和分析.X型母子型∠B∠CAC∥BD当两个三角形相似且有公共边时,借助对应边成比例往往可以得到a2=bc形式的关系.例如:“母子型”中△ABD∽△CBA→AB2=BC·BD△ACD∽△BCA→___________△ADB∽△CDA→___________实用标准文档精彩文案2.影子上墙:______________、______________、______________是影子上墙时的三种常见处理方式,它们的实质是构造三角形相似.精讲精练1.如图,在△ABC中,EF∥DC,∠AFE=∠B,AE=6,ED=3,AF=8,则AC=_________,CDBC_________.FEDCBA第1题图第2题图第3题图2.如图,AB∥CD,线段BC,AD相交于点F,点E是线段AF上一点且满足∠BEF=∠C,其中AF=6,DF=3,CF=2,则AE=_________.3.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,BD=2,AD=8,则CD=_________,AC=_________,BC=________.4.如图,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,它们的斜边长为2.若△ABC固定不动,△AFG绕点A旋转,AF,AG与边BC的交点分别为D,E(点D不与点B重合,点E不与点C重合).△DEH∽△ABC△DHG∽△ABC△HEF∽△ABCCBAGFEDHGFEDDEFGHHGFEDABDCBCDEFA实用标准文档精彩文案①请写出图中所有的相似三角形_____________________;②若BD12,则CE=________.4.如图,M为线段AB上一点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AE于点F,ME交BD于点G.(1)写出图中的三对相似三角形;(2)连接FG,当AM=MB时,求证:△MFG∽△BMG.5.如图,在矩形ABCD中,对角线AC,BD相交于点O,E为AD的中点,连接BE交AC于点F,连接FD.若∠BFA=90°,给出以下三对三角形:①△BEA与△ACD;②△FED与△DEB;③△CFD与△ABO.其中相似的有_____________(填写序号).OFEDCBAGABCDEFMGFEDCBA实用标准文档精彩文案6.如图,在△ABC中,∠ACB=90°,CE⊥AB于点E,D在AB的延长线上,且∠DCB=∠A,BD:CD=1:2,455AE,则△BCD的面积是()A.13B.53C.23D.253DBECA7.如图,在Rt△ABD中,过点D作CD⊥BD,垂足为D,连接BC交AD于点E,过点E作EF⊥BD于点F,若AB=15,CD=10,则BF:FD=_____________.FEBCDANMEDCBA第8题图第9题图8.如图,在□ABCD中,E为BC的中点,连接AE,AC,分别交BD于M,N,则BM:DN=_____________.9.如图,直线l1∥l2,若AF:FB=2:3,BC:CD=2:1,则CE:AE=_________.GFEDCBAl1l2ABCDEFG第10题图第11题图10.如图,在□ABCD中,E是BA延长线上一点,CE分别与AD,BD交于点G,F.则下列结论:①EGAGGCGD;②EFBFFCFD;③FCBFGFFD;④2CFGFEF.其中正确的是_________.实用标准文档精彩文案11.如图所示,AB∥CD,AD,BC相交于点E,过E作EF∥AB交BD于点F.则下列结论:①△EFD∽△ABD;②EFBFCDBD;③1EFEFFDBFABCDBDBD;④111ABCDEF.其中正确的有___________.FEDCBA图212.如图,在△ABC中,CD⊥AB于点D,正方形EFGH的四个顶点都在△ABC的边上.求证:111ABCDEF.HGFEDCBA13.数学兴趣小组想测量一棵树的高度.在阳光下,一名同学测得一根长为1米的竹竿的影长为0.8米,...