理论力学习题1VIP专享VIP免费

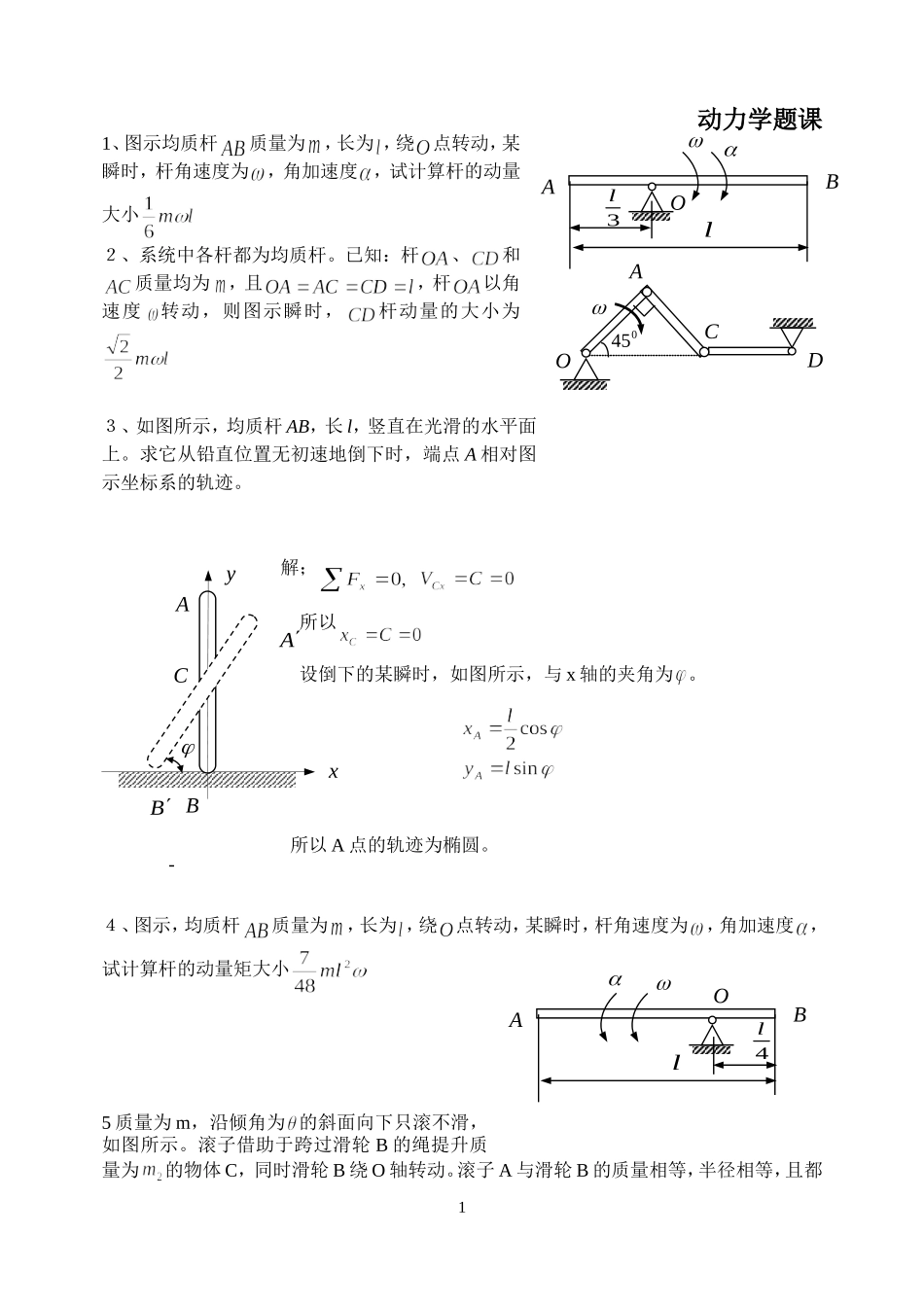
动力学题课1、图示均质杆质量为，长为，绕点转动，某瞬时，杆角速度为，角加速度，试计算杆的动量大小２、系统中各杆都为均质杆。已知：杆、和质量均为，且，杆以角速度转动，则图示瞬时，杆动量的大小为３、如图所示，均质杆AB，长l，竖直在光滑的水平面上。求它从铅直位置无初速地倒下时，端点A相对图示坐标系的轨迹。解；所以设倒下的某瞬时，如图所示，与x轴的夹角为。所以A点的轨迹为椭圆。４、图示，均质杆质量为，长为，绕点转动，某瞬时，杆角速度为，角加速度，试计算杆的动量矩大小5质量为m，沿倾角为的斜面向下只滚不滑，如图所示。滚子借助于跨过滑轮B的绳提升质量为的物体C，同时滑轮B绕O轴转动。滚子A与滑轮B的质量相等，半径相等，且都1ABOl3l045CDAO-CBAyxABABOl4l为均质圆盘。求滚子重心的加速度解：设滚子质心下滑距离S时，质心的速度为以整体为研究对象，设滚子半径为R，该系统的动能为将代入，得由动能定理得，将上式两边对时间求导得6均质圆盘与杆OA焊在一起，可绕水平轴O转动，如图所示。已知杆OA长l，质量为m1；圆盘半径为R，质量为m2。摩擦不计，初始时杆OA水平，杆和圆盘静止。求杆与水平线成θ角的瞬时，杆的角速度和角加速度。2AOAAOBC7、三个均质轮、、，具有相同的质量和相同的半径，绳重不计，系统从静止释放。设轮作纯滚动，绳的倾斜段与斜面平行。试求在重力作用下，质量亦为的物体下落时的速度和加速度。3ABDC8、均质圆盘质量为m，半径为R，OC=R/2。求（1）圆盘的惯性力系向转轴O简化的结果，并绘图表示；（2）圆盘的惯性力系向质心C简化的结果，并绘图表示。解：而，，方向与加速度方向相反向轴简化：方向与相反4CωWTTmvTmrJJJrVrVrVVVrVJmVJJmVmVTTVAhAADCBBDDBCABBBDDDccBBBAA1222222222221,42121,2,2,,2121212121210的速度为时，物体下落设物体21)sin1(4a121)sin1(8)1(sin22AgghVhmgmghWA：）式两边对时间求导得将（向质心简化：9、圆柱形滚子质量为20kg，其上绕有细绳，绳沿水平方向拉出，跨过无重滑轮B系有质量为10kg的重物A，如图所示。如滚子沿水平面只滚不滑，求滚子中心C的加速度。解：，，以为研究对象：；（1）以为研究对象：；（2）联立（1）和（2）得：10、质量为的物体A下落时，带动质量为的物体B转动，不计支架和绳子的重量及轴上的摩擦，BC=a，盘B的半径为R。求固定端C的约束力。5Cω向质心C简化tCanCatICFnICFICMCω向轴O简化tCanCatIOFnIOFIOMABCABCaIBMCMIFCyFCxF2mg1mgTFCNFCaICMCmgICFSFCTFAAmgIAF解：以系统为研究对象，设下落的加速度为，则，由达朗贝尔原理：；（1）；（2）；（3）以和整体为研究对象：；（4）由（4）得：代入（2）、（3）得：，11、如图所示，边长为a的等边直角折杆AB和CD在C处铰接。画出A、B、C、D和AB、CD杆的虚位移。并给出它们之间的大小关系式。6ABCDBACDFa1P2PBrCrDrAr12、图示曲柄式压榨机的销钉B上作用有水平力F，此力位于平面ABC内。作用线平分∠ABC。设AB=BC，∠ABC=，各处摩擦及杆重不计，求对物体的压缩力。解：，；，而即：故：即得：13、在图示机构中，曲柄OA上作用一力偶，其矩为M，另在滑块D作用水平力F。机构尺寸如图所示。求当机构平衡时，力F与力偶矩M的关系。解：由得：；同理由得：；7ABCFNF由虚功原理得：其中：即得：即：故有：14、如图所示两等长杆AB与BC在点B用铰链连接，又在杆的D、E两点连一弹簧。弹簧的刚性系数为k，当距离AC=a时，弹簧内拉力为0。如在点C作用一水平力F，杆系处于平衡，求距离AC之值。解：假设弹簧原长为，平衡时为，平衡时则：，即：，即：将弹簧解除代以力，，则；；；则：；；；由虚功原理得：即：故有：15、质量为的滑块Ａ与刚度系数为ｋ的弹簧相连，可沿光滑水平面来回滑动。在滑块8ACOlBalDFMArBrDrbBlFDECxA1F2FxyＡ上又连接一单摆。摆长为，Ｂ的质量为。试列出该系统的运动微分方程。解：取弹簧原长处为弹性力...