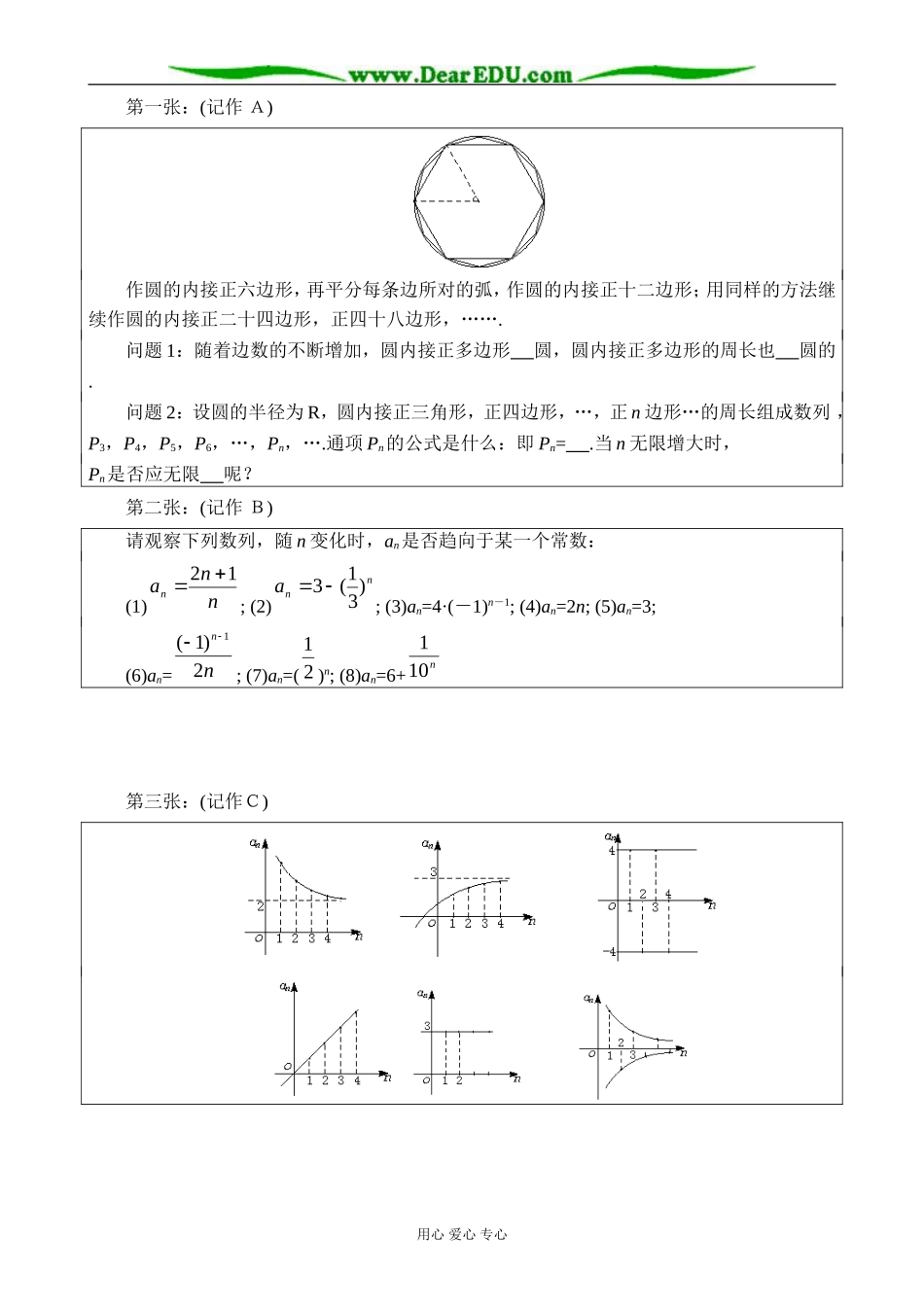
函数的极限教学目标(一)教学知识点1.数列的极限是一个十分重要的概念,它的通俗定义是:随着项数n的无限增大,数列的项an无限地趋近于某个常数a(即|an-a|无限地接近于0),它有两个方面的意义.2.ε—N定义定量地刻划了数列的项an怎样随n的无限增大而无限地趋近于常数a,要深刻理解|an-a|能任意小,并保持任意小.对于ε的理解它既具有任意性又具有相对的固定性.3.定义法求简单数列的极限.(二)能力训练要求※1.掌握数列极限的ε—N的定义.※2.会用ε—N,求数列的极限.(三)德育渗透目标1.培养学生有限与无限、精确与近似、量变与质变的辩证关系.2.培养学生数形结合、极限的数学思想方法和灵活应变的解题能力,培养学生学会利用定义解题.3.通过“割圆术”的介绍,培养学生的爱国主义精神和弘扬中华民族优秀文化的精神.教学重点理解数列的极限的直观描述方式的定义,只是对数列变化趋势的定性说明,而不是定量化的定义.“随着项数n的无限增大,数列的项an无限地趋近于某个常数a”的意义有两个方面:一方面,数列的项an趋近于a是在无限过程中进行的,即随着n的增大an越来越接近于a;另一方面,an不是一般地趋近于a,而是“无限”地趋近于a,即|an-a|随n的增大而无限地趋近于0.理解数列的极限的ε—N的定义是定量地刻划了数列的项an怎样随n的无限增大而无限地趋近于常数a.对于预先指定的任意小的正数ε,都存在一个正整数N,使得只要n>N,就有|an-a|<ε.教学难点数列的极限的ε—N定义的理解,这个定义具有一定的抽象性.数列{an}的极限为a,意味着当n无限增大时,|an-a|能任意小,并保持任意小.这就是说,对于预先给定的任意小的正数ε,都可以找到相应的N,当n>N时,|an-a|比ε还要小,即{an}中第N项以后的所有项都保持|an-a|<ε.利用数列的极限的定义求数列的极限的步骤是:求|an-a|的解析式(关于n)→求解关于n的不等式|an-a|<ε(ε是任意给定的小正数)n>n0→取n0的整数部分作为N→由定义得出nliman=a.教学方法建构主义理论指导教学法.教具准备准备三张幻灯片用心爱心专心第一张:(记作A)作圆的内接正六边形,再平分每条边所对的弧,作圆的内接正十二边形;用同样的方法继续作圆的内接正二十四边形,正四十八边形,…….问题1:随着边数的不断增加,圆内接正多边形圆,圆内接正多边形的周长也圆的.问题2:设圆的半径为R,圆内接正三角形,正四边形,…,正n边形…的周长组成数列,P3,P4,P5,P6,…,Pn,….通项Pn的公式是什么:即Pn=.当n无限增大时,Pn是否应无限呢?第二张:(记作B)请观察下列数列,随n变化时,an是否趋向于某一个常数:(1)nnan12;(2)nna)31(3;(3)an=4·(-1)n-1;(4)an=2n;(5)an=3;(6)an=nn2)1(1;(7)an=(21)n;(8)an=6+n101第三张:(记作C)用心爱心专心教学过程Ⅰ.课题导入[师]高一上学期我们学习了数列的有关概念、数列通项公式的求法,仔细研究了两个重要的数列——等差数列,等比数列.打出幻灯片A,让同学们解决下列问题:[师]按影片上的要求,我们再画出正二十四边形正四十八边形,…,从直观上看,随着边数的不断增加,圆内接正多边形与圆的关系?正多边形的周长与圆周长的关系是什么?[生1]正多边形越来越接近(逼近、趋近)于圆;圆内接正多边形的周长也就越来越接近(逼近、趋近)于圆的周长.[师]设圆的半径为R,圆内接正三角形、正四边形、正五边形、…,正n边形的周长所组成的数列P3,P4,P5,…,Pn,….则通项公式Pn=.[生2]P3=3·2RsinR333,P4=4·2RsinR244,P5=2Rsin5×5=10Rsin5,…,Pn=n·2Rsinn.[师]由图形可以直观看出当n趋向无限大时,Pn就无限地趋向于什么呢?[生3]Pn无限地趋向于2πR.[师]这也是数列的另一个重要方面,今天我们就来学习研究数列的另一个侧面:随n变化时,an是否趋向于某一个常数(虽然“趋向于”并没有确切定义,但是同学们能感觉是什么意思——由“粗”到“细”.板书:研究数列an随n变化时是否趋向于某一个常数)Ⅱ.讲授新课打出幻灯片B,请同学们观察下列数列,随n变化时,an是否趋向于某一个常数:(1)nnan12;(2)nna)31(3;(3)an=4·(-1)n-1;(4)an=2...