小结与思考-(2)VIP专享VIP免费

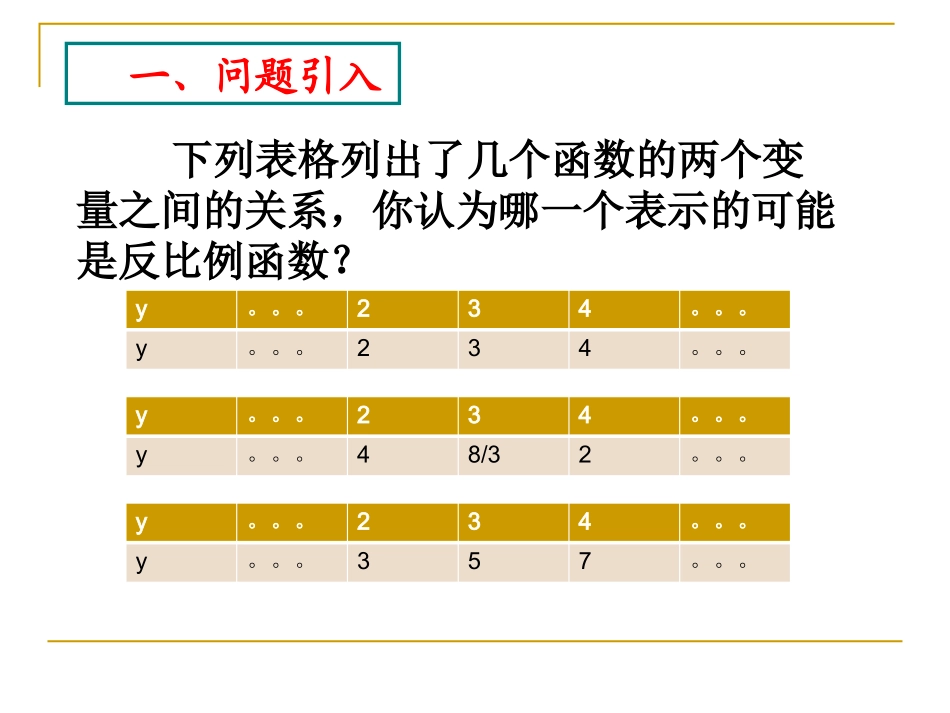
一、问题引入下列表格列出了几个函数的两个变量之间的关系，你认为哪一个表示的可能是反比例函数？y。。。234。。。y。。。48/32。。。y。。。234。。。y。。。234。。。y。。。234。。。y。。。357。。。形如的函数叫做反比例函数。xky（k≠0,k为常数）xkyy=kx-1xy=k（k≠0）（k≠0）等价形式：（k≠0）二、知识复习反比例函数的图象既是_________又是___________。有________对称轴，对称中心是：____xy012y=—kxy=xy=-x轴对称图形中心对称图形原点●两条K>0K<0函数图象的两个分支分别在第一、三象限函数图象的两个分支分别在第二、四象限，图象位置y=xk渐近性在每个象限内，y随x的增大而减小.在每个象限内，y随x的增大而减小.当x值的绝对值无限增大或接近于零时，它的两个分支都无限接近x轴或y轴，但永远不会与x轴y轴相交。增减性1||2OAPSkyP(m,n)AoxByAP(m,n)oxP(m,n)oyxBP(m,n)AoxBy||||||||knmnmAPOASOAPB矩形xky例1.结合函数，提出并解决问题x8y三、典例分析例2.直线与反比例函数的图像交于A、B两点。(1)若A(2,4),你能说出点B的坐标么？(2)在(1)的条件下，结合图像方程的解？不等式中x的取值范围？kxyx8yxA(2,4)BOykxx8kxx8例3.如图，在平面直角坐标系中，A为y轴正半轴上一点，过A作x轴的平行线，交函数的图象于B，交函数的图象于C，过C作y轴的平行线交x轴于D．四边形BODC的面积为．2(0)yxx9)0(8xxyxy8例4.为了预防“流感”,某学校对教室采用药熏消毒法进行毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例.药物燃烧后,y与x成反比例(如图所示),现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg,请根据题中所提供的信息,解答下列问题:(1)药物燃烧时,y关于x的函数关系式为:________,自变量x的取值范围是:__________,药物燃烧后y关于x的函数关系式为_____________.kxy：设解xk43y4368）代入，求出，将点（xky式为根据图像，设函数解析)8(48y4868xxk）代入，求出，将点（)8(48xxyxy4380x6O8x(min)y(mg)为了预防“流感”,某学校对教室采用药熏消毒法进行毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例.药物燃烧后,y与x成反比例(如图所示),现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg,请根据题中所提供的信息,解答下列问题:(2)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?1.先求出教室中含氧量为3mg时的时间点xy434xxy4816x2.再从图像中发现，当消毒过程处于这两个时间点之间时，教室中的含药量是大于等于3mg。3.将两个时间点相减后与10比较，发现本次消毒是有效的。例5.函数的图像函数的图像xy1xyx8y1-x8y1.已知点A(-2,y1),B(-1,y2)都在反比例函数的图象上,则y1与y2的大小关系(从大到小)为.x4yxky(k＜0)y2＞y12.已知点A(-2,y1),B(-1,y2)都在反比例函数的图象上,则y1与y2的大小关系(从大到小)为.x4yxky(k＜0)A(x1,y1),B(x2,y2)且x1＜0＜x2yxox1x2Ay1y2By1＞y2２3、点A和点B在反比例函数上且线段AB经过点O,过点A、B分别作直线AC、BC平行于Y轴和X轴,两直线交于点C,则SABC⊿的面积=____如图、一次函数y1=ax+b的图象和反比例函数的图象交于A(3,1)、B(n,-3)两点.(1)求反比例函数和一次函数的解析式。(2)x取何值时,y1y﹥2。AB_kxy2=yxoy1=ax+b_kxy2=(2)当x3﹥或-1x0﹤﹤时,y1y﹥2。1C-13综合运用四、小结与思考1.反比例函数解析式常见的几种形式:2.反比例函数图像的形状，位置，增减性,对称性，面积不变性。3.一些基本题型的解题要点4.反比例函数在生活中的应用5.做题时要注意数形结合1、必做题：一张试卷2、选做题：心理学家研究发现，一般情况下，一节课40分钟中，学生的注意力随教师讲课的变化而变化．开始上课时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的稳定状态，随后学生的注意力开始分散．经过实验分析可知，学生的注意力指标数y随时间x（分钟）的变化规律如右图所示（注：AB段为...