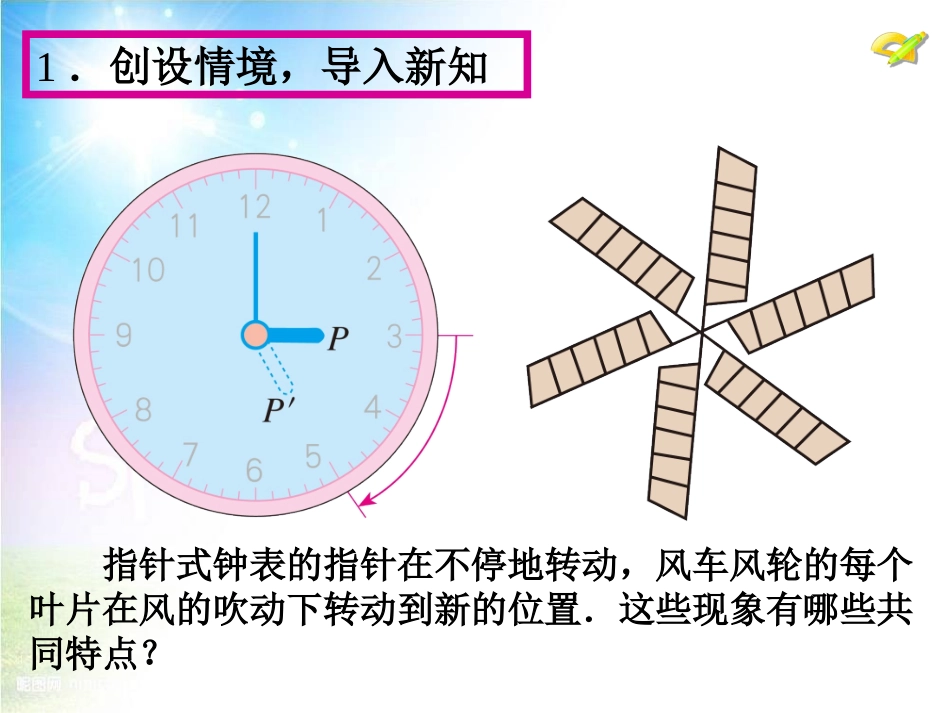
23.1图形的旋转九年级上册•学习目标:1.通过观察具体实例学习旋转概念,会画一个图形作旋转后所得的图形;2.探究旋转的性质,并在观察、猜想、验证、归纳、概括的探究过程中,发展合情推理能力,进一步体会图形运动中的变和不变.·学习重点:旋转的性质.1.创设情境,导入新知指针式钟表的指针在不停地转动,风车风轮的每个叶片在风的吹动下转动到新的位置.这些现象有哪些共同特点?OP′P2.定义120°把一个平面图形绕着平面内某一点O转动一个角度的图形变换叫做图形的旋转.这个点O叫旋转中心,转动的角叫做旋转角.如果图形上的点P经过旋转变为点P′,那么这两个点叫做这个旋转的对应点.1.时钟的时针在不停地转动,从上午6时到上午9时,时针旋转的旋转角是多少度?从上午9时到上午10时呢?3.小试牛刀2.如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?3.小试牛刀4.探究在硬纸板上,挖一个三角形洞,再另挖一个小洞O作为旋转中心,硬纸板下面放一张白纸,先在纸上描出这个挖掉的三角形图案(△ABC),然后围绕旋转中心转动硬纸板,再描出这个挖掉的三角形(△ABC),移开硬纸板.请同学们思考以下问题:'''4.探究(1)△ABC可以看作△ABC经过怎样的运动得到的?(2)线段OA和OA'有什么关系?∠AOA'和∠BOB'有什么关系?(3)你还能发现哪些有类似关系的线段和角?''''''(4)△ABC和△ABC的形状和大小有什么关系?4.探究(5)这一发现对于任意三角形的任意旋转都成立吗?(6)你能把以上发现,用自己的语言归纳概括一下吗?4.探究◆对应点到旋转中心的距离相等.◆对应点与旋转中心所连线段的夹角等于旋转角.◆旋转前、后的图形全等.旋转的性质ABO5.应用例1下图为4×4的正方形网格,每个小正方形的边长均为1,将△OAB绕点O逆时针旋转90°,你能画出△OAB旋转后的图形△OAB吗?'''A'B'(1)如何画出旋转后的图形?(2)如何确定旋转后的对应点的位置?6.归纳总结例2如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,你能画出旋转后的图形吗?试一试你有几种方法?7.应用ABCED方法1:F图中△ABF为所求图形.7.应用ABCED方法2:F图中△ABF为所求图形.7.应用ABCED方法3:F图中△ABF为所求图形.7.应用ABCED对比平移、轴对称,旋转的性质,它们有哪些相同点和不同点?8.小结教科书习题23.1第1,4,5题.9.布置作业