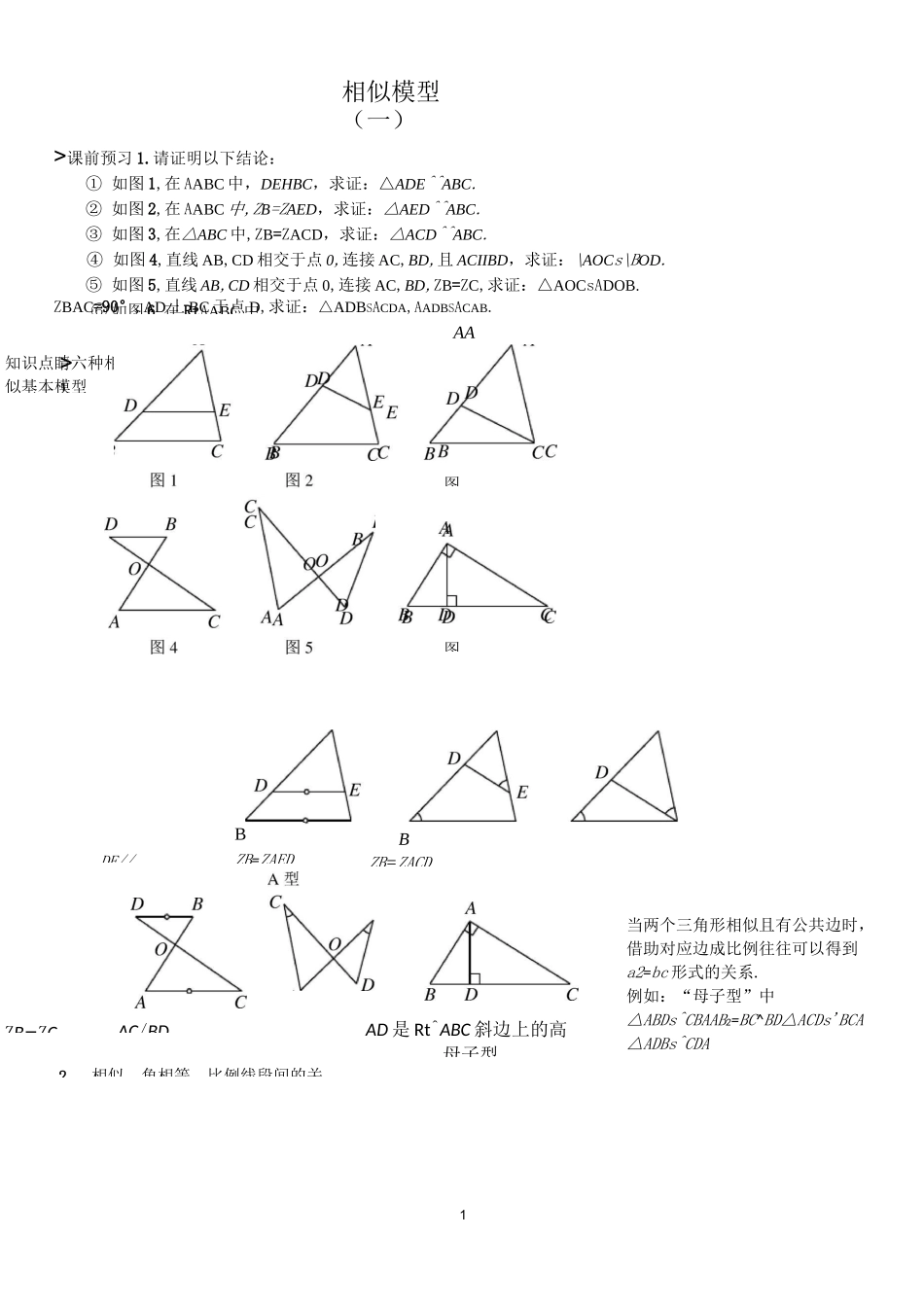
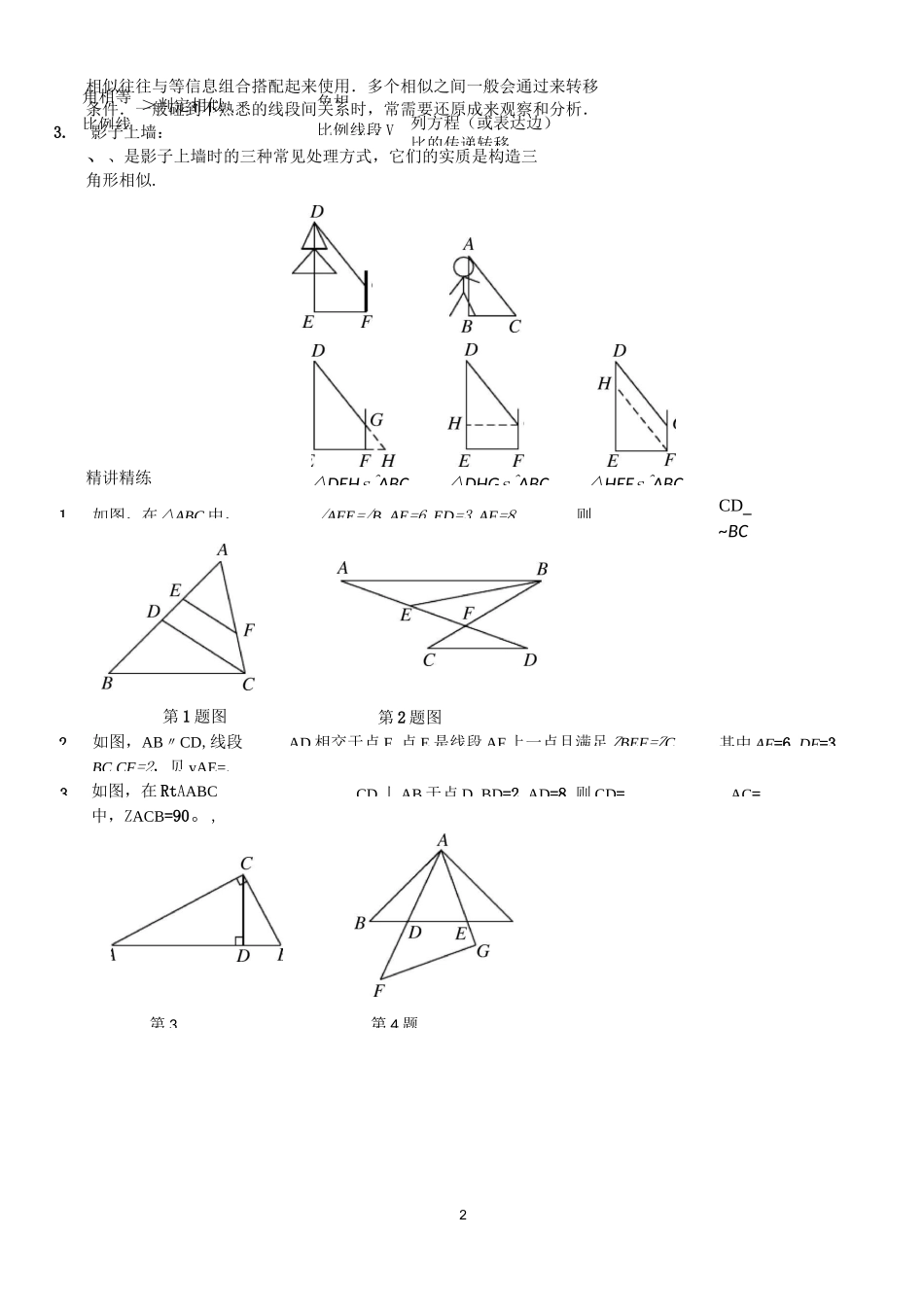
1>12知识点睛六种相似基本模型DE//BZB=ZACDAC/BDZB=ZCAD是Rt^ABC斜边上的高母子型相似、角相等、比例线段间的关当两个三角形相似且有公共边时,借助对应边成比例往往可以得到a2=bc形式的关系.例如:“母子型”中△ABDs^CBAAB2=BC^BD△ACDs'BCA△ADBs^CDA⑥如图6,在RtAABC中,>课前预习1.请证明以下结论:①如图1,在AABC中,DEHBC,求证:△ADE^^ABC.②如图2,在AABC中,ZB=ZAED,求证:△AED^^ABC.③如图3,在△ABC中,ZB=ZACD,求证:△ACD^^ABC.④如图4,直线AB,CD相交于点0,连接AC,BD,且ACIIBD,求证:\AOCs\BOD.⑤如图5,直线AB,CD相交于点0,连接AC,BD,ZB=ZC,求证:△AOCsADOB.ZBAC=90°,AD丄BC于点D,求证:△ADBSACDA,AADBSACAB.AA相似模型(一)图图BZB=ZAED2角相等比例线>判定相似角相比例线段V列方程(或表达边)比的传递转移△DEHs^ABC△DHGs^ABC△HEFs^ABC1如图,在△ABC中,/AFE=/B,AE=6,ED=3,AF=8,则CD_~BC23第1题图如图,AB〃CD,线段BC,CF=2,贝yAE=.第2题图AD相交于点F,点E是线段AF上一点且满足ZBEF=ZC,其中AF=6,DF=3,如图,在RtAABC中,ZACB=90。,CD丄AB于点D,BD=2,AD=8,则CD=,AC=第3相似往往与等信息组合搭配起来使用.多个相似之间一般会通过来转移条件.一般碰到不熟悉的线段间关系时,常需要还原成来观察和分析.3.影子上墙:、、是影子上墙时的三种常见处理方式,它们的实质是构造三角形相似.精讲精练第4题(填写序号).AEDBC7A.3C.3D34.如图,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,ZBAC=ZAGF=90。,它们的斜边长为2,若△ABC固定不动,AAFG绕点A旋转,AF,AG与边BC的交点分别为D,E(点D不与点B重合,点E不与点C重合).①请写出图中所有的相似三角形;②若BD二-,则CE=厶5.如图,M为线段AB上一点,AE与BD交于点C,/DME=/A=/B=a,且DM交AE于点F,ME交BD于点G.(1)写出图中的三对相似三角形;(2)连接FG,当AM=MB时,求证:△MFGS^BMG.6.如图,在矩形ABCD中,对角线AC,BD相交于点0,E为AD的中点,连接BE交AC于点F,连接FD.若ZBF4=90°,给出以下三对三角形:①△BEA与△ACD;②厶FED与ADEB;③厶CFD与AABO.其中相似的有如图,在AABC中,ZACB=90°,CE丄AB于点E,D在AB的延长线上,且ZDCB=ZA,BDCD=12,AE二则ABCD的面积是()8.如图,在RtAABD中,过点D作CD丄BD,垂足为D,连接BC交AD于点E,过点E作EF丄BD于点F,若第8题图第9题图9.如图,在DABCD中,E为BC的中点,连接AE,AC,分别交BD于M,N,则BMDN=10.如图,直线IJ/y若AFFB=23,BCCD=21,则CEAE=.第10题图第11题图EGAG11.如图,在□ABCD中,E是BA延长线上一点,CE分别与AD,BD交于点G,F.则下列结论:①=—-EFBFFCBF③疋二冷;④CF2=GF-EF•其中正确的是12.如图所示,AB〃CD,AD,BC交于点E,过E作EFAB交BD于点F.则下列结论:①△EFDsgBD;②EFBFEFEFFDBF111—;③+—+—1:④+—.其CDBDABCDBDBDABCDEF图13.如图,在△ABC中,CD丄AB于点D,正方形EFGH的四个顶点都在AABC的边上.求证:丄+丄二丄;ABCDEF14.数学兴趣小组想测量一棵树的高度.在阳光下,一名同学测得一根长为1米的竹竿的影长为0.8米,同时另一部分影长为1.2米,落在地面上的影长为2.4米,则树高为A.9米C.(7+筋)米D.(14+2⑦米4第14题图第15题图15.小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上,量得CD=8米,BC=20米,CD与地面成30°角,且此时测得1米杆的影长为2米,则电线杆的高度为()B.28米16.如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.若铁塔底座宽CD=12m,塔影长DE=18m,小明和小lD似三角形(不包括全若ZAPB=120°,请找5华的身高都是1.6m,同一时刻小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m和1m,则塔高AB为()A.24mB.22mC.20mD.18m相似模型(二)课前预习1.按要求解决下列问题:①如图,AB丄BD于点B,ED丄BD于点D,点C是线段BD上一点,连接AC,CE,ACLCE.求证:△ABCs^CDE.②如图,将两个全等的等腰直角三角形如图摆放(顶点A重合),所有的点都在同一平面内•请找出图中的相QR>知识点睛1.相似综合模型②平行结构一一作平行,得相似(构...