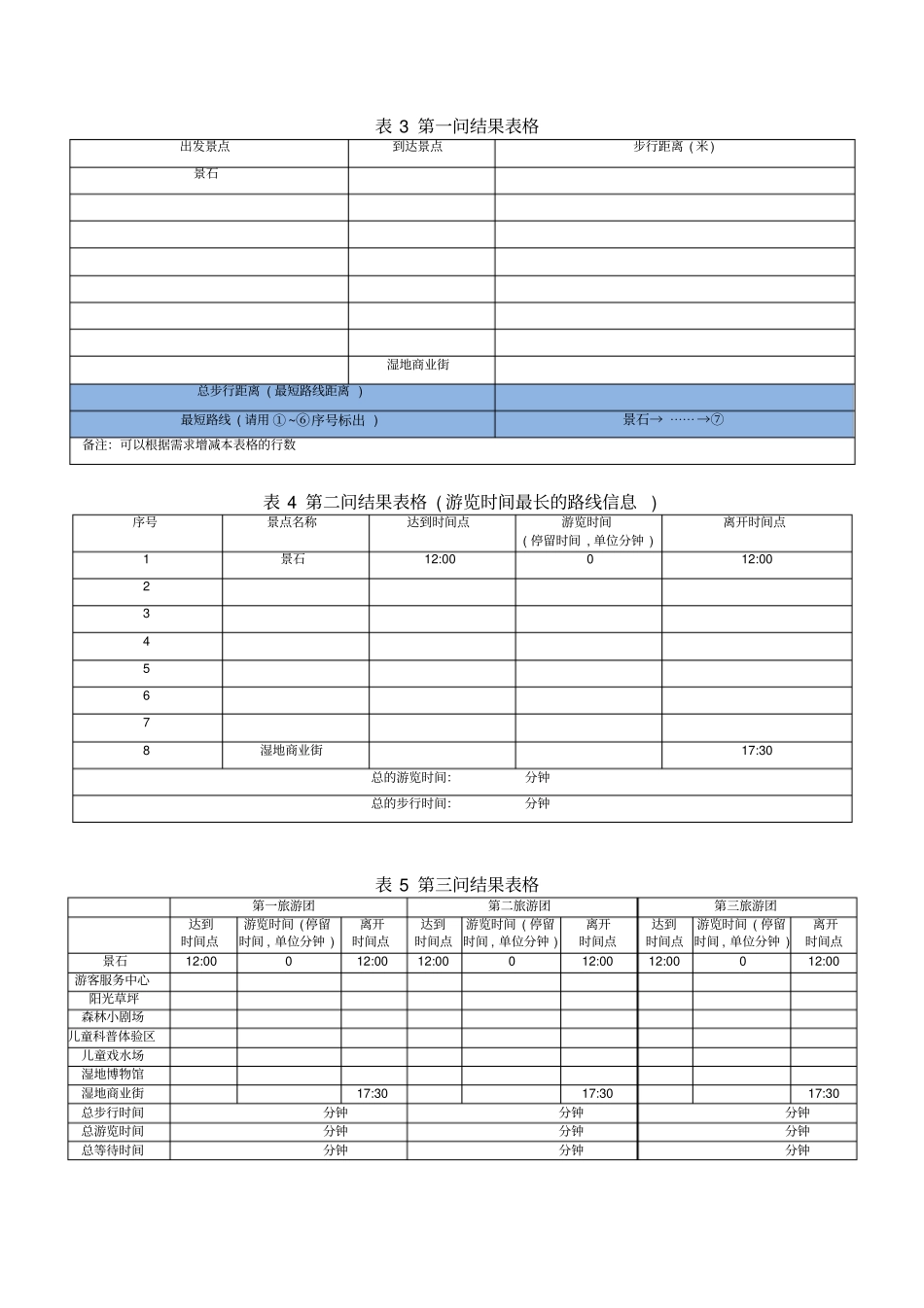
A题安略湖风景区游览路线设计随着人们生活水平的提高,旅游成为人们日常生活中不可或缺的部分。各地绿色生态建设也提到议事日程,某市在自然资源条件下开发建设安略湖风景区,安略湖景区的部分景点(如图1所示),为了方便游客观光,提高景区资源利用率,请在如下的假设下,完成安略湖风景区游览路线设计问题。假设:(1)任意两个景点之间的最短步行距离如表1给出。(2)第二问、第三问假设步行速度2/Vkmh。(3)游客在景区停留的时间由“景点之间的步行时间”、“景点游览时间(即在景点内游玩的时间)”和“在景区外的等待时间”三部分组成,其他时间忽略不计,游览时间必须符合表2的要求。问题:1.从景石出发,步行游览以下景点:①游客服务中心,②阳光草坪,③森林小剧场,④儿童科普体验区,⑤儿童戏水场,⑥湿地博物馆,⑦湿地商业街。建立数学模型,找出从景石出发,到达⑦湿地商业街,并且经过①—⑥所有景点至少1次的距离最短的路线,计算该路线的长度,并将相关结果填入表格3。注:在每个景点不用停留。2.如果某游客12:00从景石出发,要求他17:00前到达湿地商业街,17:30离开湿地商业街(注:根据表2的要求在湿地商业街游览时间至少为30分钟)。建立数学模型,为该游客设计一条能游览完全部景点(景点①—⑦)且游览总时间最长的游览路线(假设在各个景点没有等待时间),并完成表4的填写。3.如果有3个旅游团,12:00同时从景石出发,要求三个旅游团17:00前到达湿地商业街,17:30离开湿地商业街(注:根据表2的要求在湿地商业街游览时间至少为30分钟),并且每个景点(湿地商业街除外)同时只能容纳1个旅游团游览,按照时间顺序后到达的旅游团,需要等待先到达的旅游团游览结束之后才能开始游览。建立数学模型,为三个旅游团分别设计一条能游览完全部7个景点且游览总时间最长的游览路线,并完成表5的填写。4.假设3个旅游团的步行速度可以在1/kmh到3/kmh之间调节,但是总的平均步行速度不能超过2/kmh,3个旅游团12:00同时从景石出发,要求三个旅游团17:00前到达湿地商业街,17:30离开湿地商业街(注:根据表2的要求在湿地商业街游览时间至少为30分钟),并且每个景点(湿地商业街除外)同时只能容纳1个旅游团游览,按照时间顺序后到达的旅游团,需要等待先到达的旅游团游览结束之后才能开始游览。建立数学模型,为三个旅游团分别设计一条能游览完全部7个景点且游览总时间长,总的等待时间短的游览路线,并完成表6的填写。5.在现实中,考虑如下两个不确定性因素(1)不同旅游团从景石出发的时间具有不确定性,例如,多个旅游团在不同的时间从景石出发开始游览,在此情况下到达湿地商业街的时间可以顺延。(2)每个景点的等待时间也存在不确定性因素,例如,旅游设施短时间的维护和清理,或者受到散客客流的影响。考虑上述两个不确定性因素,其它条件与问题4相同,建立数学模型,为多个旅游团分别设计一条能游览完全部7个景点且游览总时间长,总的等待时间短的游览路线。图1各景点位置示意图表1景点之间的最短步行距离(单位:米)景石游客服务中心阳光草坪森林小剧场儿童科普体验区儿童戏水场湿地博物馆湿地商业街景石0300360210590475500690游客服务中心3000380270230285200390阳光草坪3603800510230765580770森林小剧场2102705100470265450640儿童科普体验区5902302304700515360550儿童戏水场4752857652655150460650湿地博物馆5002005804503604600190湿地商业街6903907606405506501900表2各景点游览时间时间景点游览时间开放时间游客服务中心10-30分钟9:00-16:00阳光草坪20-60分钟9:00-17:00森林小剧场30分钟9:00,9:30,10:00,10:30,11:00,11:30,12:00,12:30,13:00,13:30,14:00,14:30,15:00,15:30,16:00,16:30,17:00(半点和整点开放)儿童科普体验区30-60分钟9:00-17:00儿童戏水场20-60分钟9:00-17:00湿地博物馆30-60分钟9:00-17:00湿地商业街30分钟以上9:00-21:30表3第一问结果表格出发景点到达景点步行距离(米)景石湿地商业街总步行距离(最短路线距离)最短路线(请用①~⑥序号标出)景石→⋯⋯→⑦备注:可以根据需求增减本表格的行数表4第二问结果表格(游览时间最长的路线信息)序号景点名...