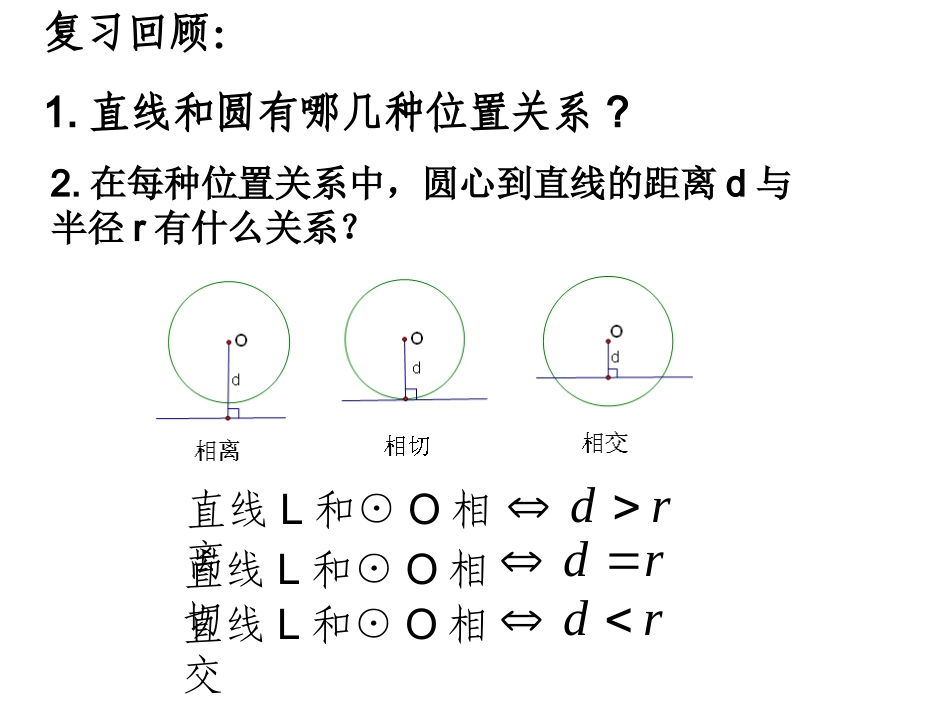
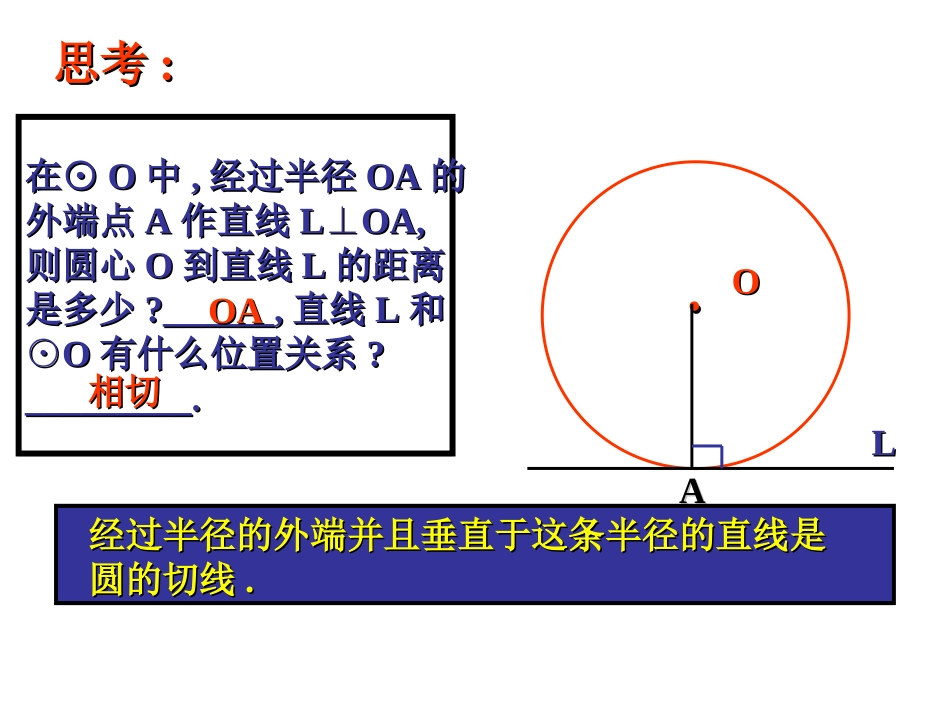
切线的性质和判定l复习回顾:直线L和⊙O相离rd直线L和⊙O相切rdrd直线L和⊙O相交1.直线和圆有哪几种位置关系?2.在每种位置关系中,圆心到直线的距离d与半径r有什么关系?在⊙在⊙OO中中,,经过半径经过半径OAOA的的外端点外端点AA作直线作直线LOA,⊥LOA,⊥则圆心则圆心OO到直线到直线LL的距离的距离是多少是多少?______,?______,直线直线LL和和⊙⊙OO有什么位置关系有什么位置关系??_________._________.思考思考::..OOAAOAOA相切相切LL经过半径的外端并且垂直于这条半径的直线是经过半径的外端并且垂直于这条半径的直线是圆的切线圆的切线..切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.(两个条件缺一不可)几何语言:∵ABOE⊥,OE是⊙O的半径∴AB是⊙O的切线证明相切的常用思路:(两种辅助线的做法)①若明确直线和圆的公共点,我们作半径(连接公共点和圆心),去证明这条半径和直线垂直;②若不明确直线和圆的公共点,我们过圆心作这条直线的垂线,去证明垂线段等于半径.切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.切线的性质定理:圆的切线垂直于经过切点的半径.几何语言:∵AB是⊙O的切线,E为切点∴ABOE⊥(常用的辅助线是连接圆心和切点)例例11直线直线ABAB经过⊙经过⊙OO上的点上的点C,C,并且并且OA=OB,CA=CB,OA=OB,CA=CB,求证求证::直线直线ABAB是⊙是⊙OO的切线的切线..证明证明::连接连接OCOC∵∵OA=OB,CA=CBOA=OB,CA=CB∴△∴△OABOAB是等腰三角形是等腰三角形,OC,OC是底边是底边ABAB上的中线上的中线∴∴OCAB⊥OCAB⊥∴∴ABAB是⊙是⊙OO的切线的切线例2.如图,在RtABC△中,BCA=90°,∠以BC为直径的⊙O交AB于点P,Q是AC的中点.判断直线PQ与⊙O的位置关系,并说明理由.解:例3、①如图,已知:AB为⊙O的直径,直线AC和⊙O相切于A点,AP为⊙O的一条弦.求证:CAP=B∠∠另外,如右上图,若将①条件改为AB为⊙O的弦,那么结论还成立吗?说明理由。1、(2007浙江)如图:PA切⊙O于点A,该圆的半径为3,PO=5,则PA的长等于4A0P2、(2007孝感)如图:AB是⊙O上的两点,AC是⊙O的切线,∠B=700,则∠BAC=OAB200填空:填空:C(2)(1)(3)4.(2007年泸州)已知AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD.求证:DC是⊙O的切线.•∵OD=OB,OC=OC,•∴△ODC≌△OBC.•∴∠ODC=∠OBC.CBADO1234证明:连结OD.∵BC是⊙O的切线,∴∠OBC=90°.∵OA=OD,∴∠1=∠2,∵AD∥OC,∴∠1=∠3,∠2=∠4∴∠3=∠4.∴∠ODC=90°.∴DC是⊙O的切线.