建模习题及答案课后习题VIP免费

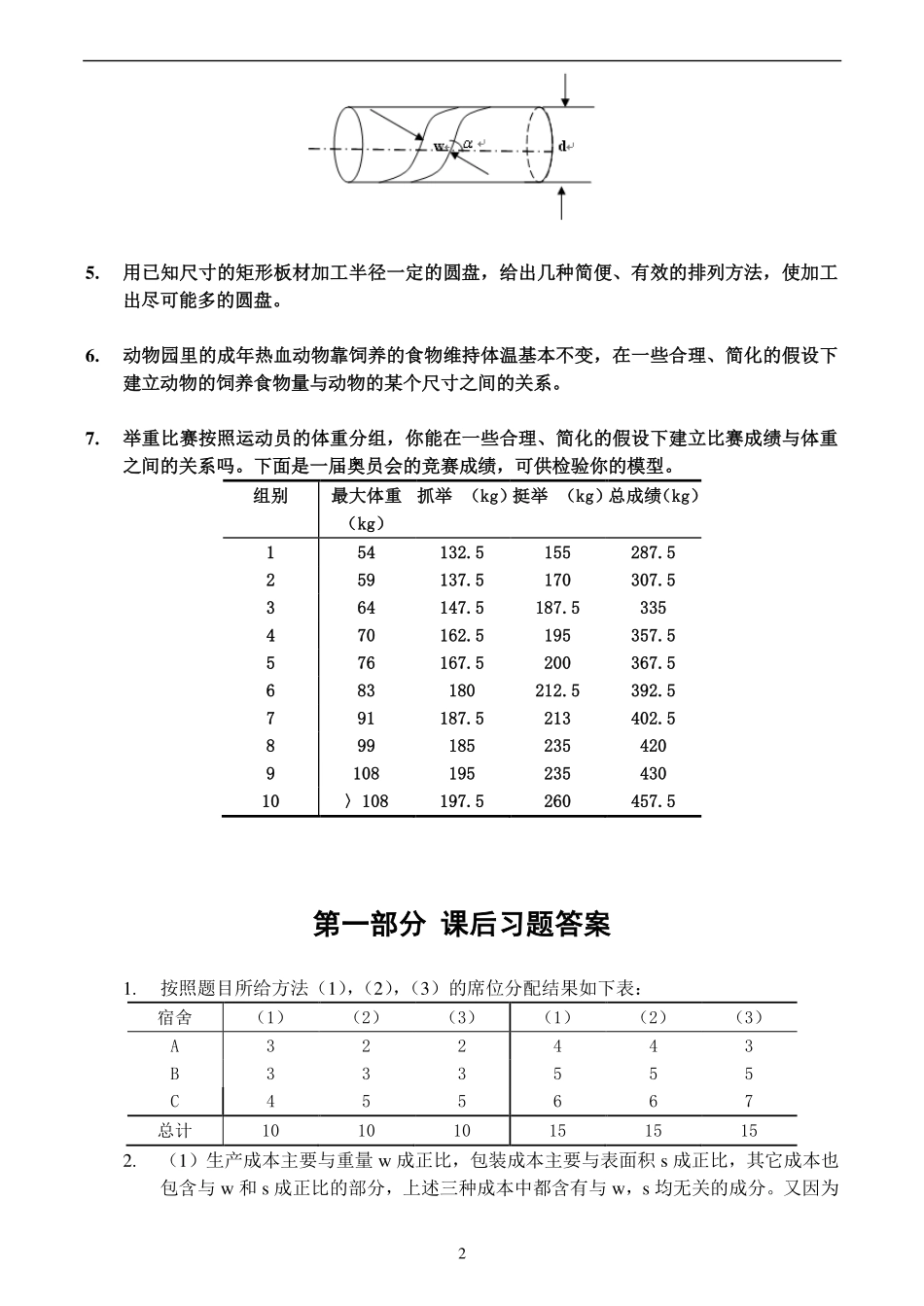
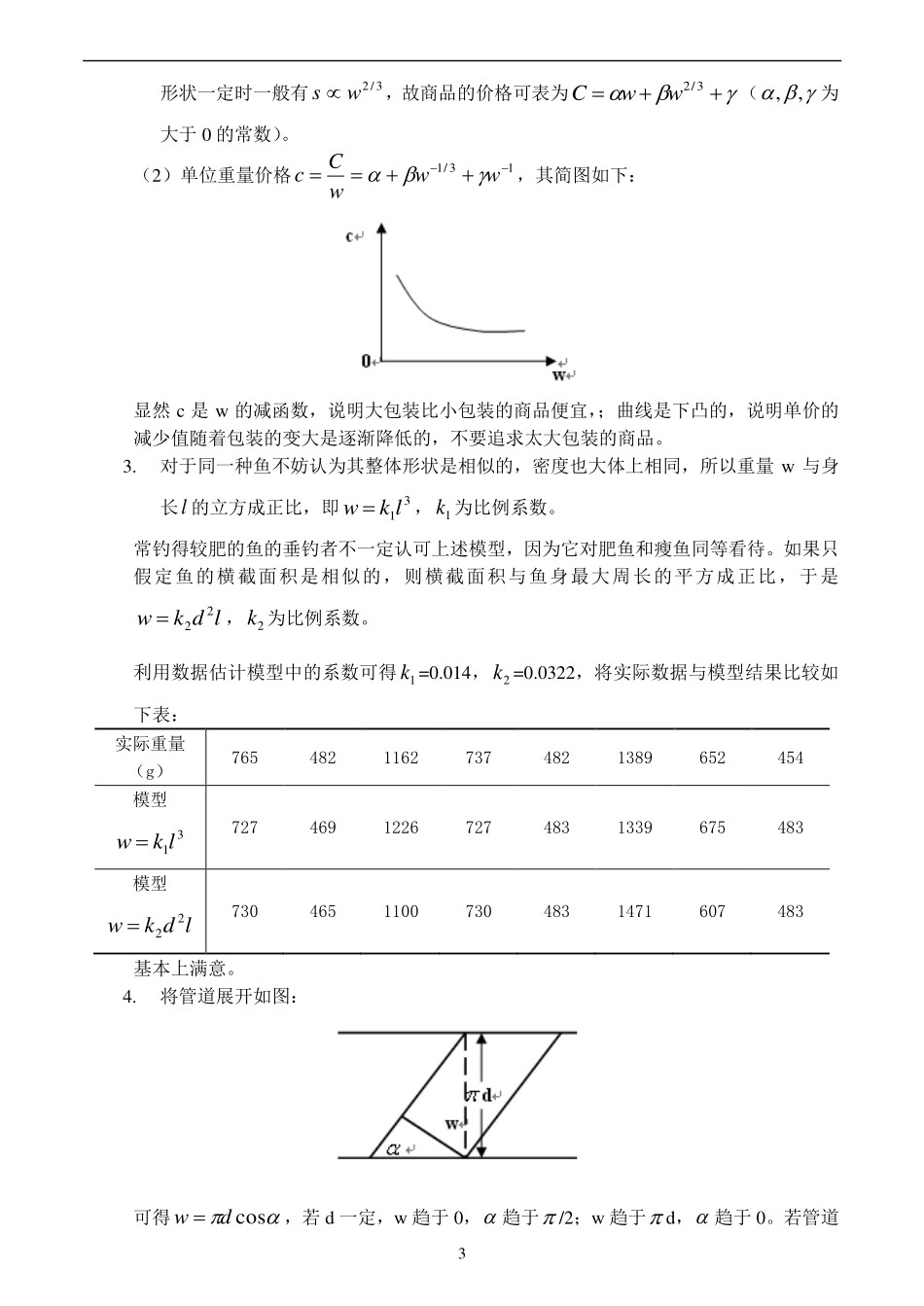
1第一部分课后习题1.学校共1000名学生，235人住在A宿舍，333人住在B宿舍，432人住在C宿舍。学生们要组织一个10人的委员会，试用下列办法分配各宿舍的委员数：（1）按比例分配取整数的名额后，剩下的名额按惯例分给小数部分较大者。（2）2.1节中的Q值方法。（3）d’Hondt方法：将A，B，C各宿舍的人数用正整数n=1，2，3，„相除，其商数如下表：12345„A235117.578.358.75„B333166.511183.25„C43221614410886.4将所得商数从大到小取前10个（10为席位数），在数字下标以横线，表中A，B，C行有横线的数分别为2，3，5，这就是3个宿舍分配的席位。你能解释这种方法的道理吗。如果委员会从10人增至15人，用以上3种方法再分配名额。将3种方法两次分配的结果列表比较。（4）你能提出其他的方法吗。用你的方法分配上面的名额。2.在超市购物时你注意到大包装商品比小包装商品便宜这种现象了吗。比如洁银牙膏50g装的每支1.50元，120g装的3.00元，二者单位重量的价格比是1.2：1。试用比例方法构造模型解释这个现象。（1）分析商品价格C与商品重量w的关系。价格由生产成本、包装成本和其他成本等决定，这些成本中有的与重量w成正比，有的与表面积成正比，还有与w无关的因素。（2）给出单位重量价格c与w的关系，画出它的简图，说明w越大c越小，但是随着w的增加c减少的程度变小。解释实际意义是什么。3.一垂钓俱乐部鼓励垂钓者将调上的鱼放生，打算按照放生的鱼的重量给予奖励，俱乐部只准备了一把软尺用于测量，请你设计按照测量的长度估计鱼的重量的方法。假定鱼池中只有一种鲈鱼，并且得到8条鱼的如下数据（胸围指鱼身的最大周长）：身长（cm）36.831.843.836.832.145.135.932.1重量（g）76548211627374821389652454胸围（cm）24.821.327.924.821.631.822.921.6先用机理分析建立模型，再用数据确定参数4.用宽w的布条缠绕直径d的圆形管道，要求布条不重叠，问布条与管道轴线的夹角应多大（如图）。若知道管道长度，需用多长布条（可考虑两端的影响）。如果管道是其他形状呢。25.用已知尺寸的矩形板材加工半径一定的圆盘，给出几种简便、有效的排列方法，使加工出尽可能多的圆盘。6.动物园里的成年热血动物靠饲养的食物维持体温基本不变，在一些合理、简化的假设下建立动物的饲养食物量与动物的某个尺寸之间的关系。7.举重比赛按照运动员的体重分组，你能在一些合理、简化的假设下建立比赛成绩与体重之间的关系吗。下面是一届奥员会的竞赛成绩，可供检验你的模型。组别最大体重（kg）抓举（kg）挺举（kg）总成绩（kg）154132.5155287.5259137.5170307.5364147.5187.5335470162.5195357.5576167.5200367.5683180212.5392.5791187.5213402.5899185235420910819523543010〉108197.5260457.5第一部分课后习题答案1.按照题目所给方法（1），（2），（3）的席位分配结果如下表：宿舍（1）（2）（3）（1）（2）（3）A322443B333555C455667总计1010101515152.（1）生产成本主要与重量w成正比，包装成本主要与表面积s成正比，其它成本也包含与w和s成正比的部分，上述三种成本中都含有与w，s均无关的成分。又因为3形状一定时一般有3/2ws，故商品的价格可表为3/2wwC（,,为大于0的常数）。（2）单位重量价格13/1wwwCc，其简图如下：显然c是w的减函数，说明大包装比小包装的商品便宜，；曲线是下凸的，说明单价的减少值随着包装的变大是逐渐降低的，不要追求太大包装的商品。3.对于同一种鱼不妨认为其整体形状是相似的，密度也大体上相同，所以重量w与身长l的立方成正比，即31lkw，1k为比例系数。常钓得较肥的鱼的垂钓者不一定认可上述模型，因为它对肥鱼和瘦鱼同等看待。如果只假定鱼的横截面积是相似的，则横截面积与鱼身最大周长的平方成正比，于是ldkw22，2k为比例系数。利用数据估计模型中的系数可得1k=0.014，2k=0.0322，将实际数据与模型结果比较如下表：实际重量（g）76548211627374821389652454模型31lkw72746912267274831339675483模型ldkw2273046511007304831471607483基本上满意。4.将管道展开如图：可得cosdw，若d一定，w趋于0，趋于...