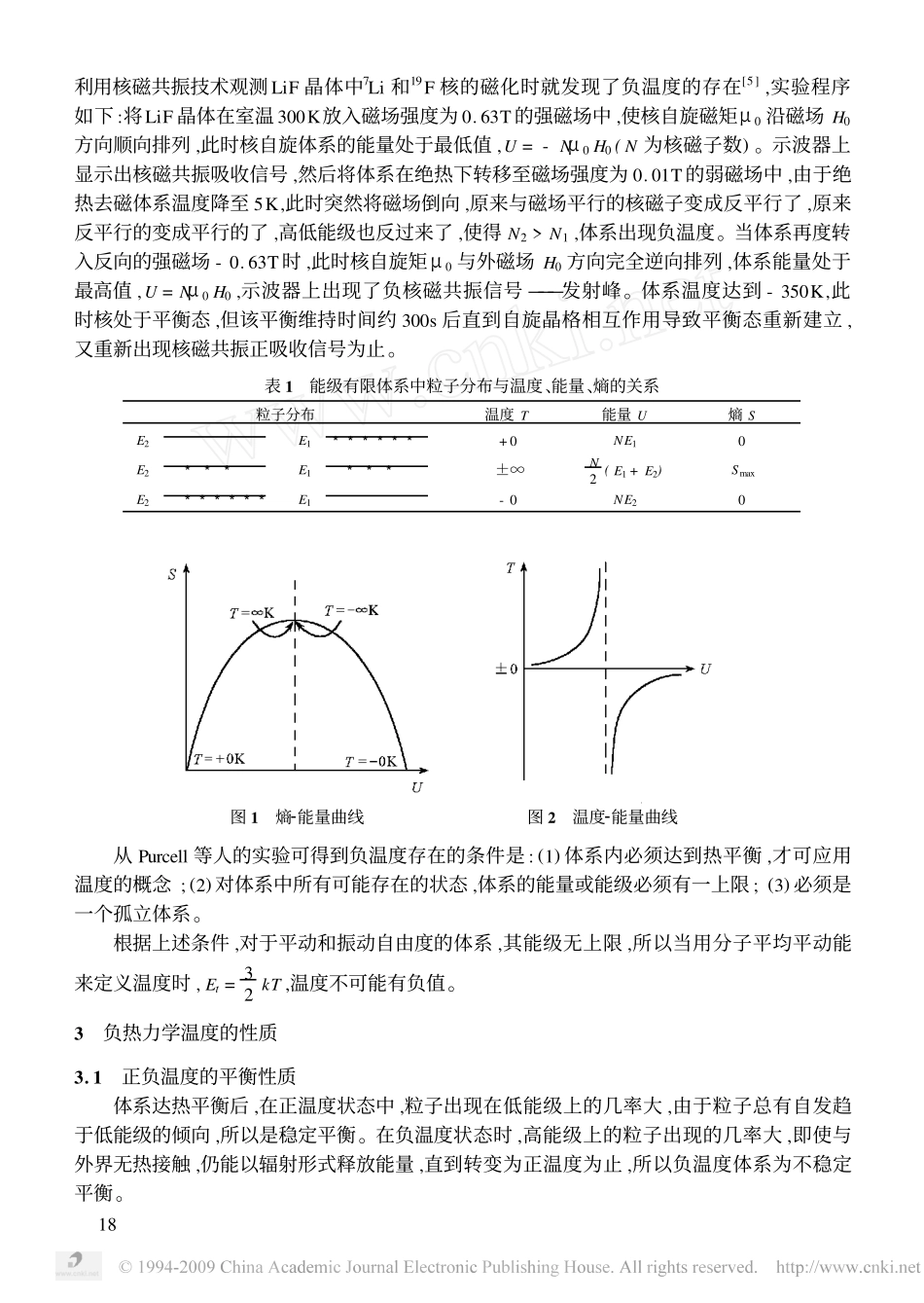
第16卷第3期大学化学2001年6月教学研究与改革负热力学温度孙德坤(南京大学化学化工学院南京210093)摘要本文从热力学基本关系式(5S/5U)V=1/T和Boltzmann分布式N2/N1=exp(-ε/kT)阐明了热力学温度不仅可以有正值还可以存在负值。以核自旋平衡体系为实例指出了负温度存在的必要条件:必须是一个能量(或能级)有上限的热平衡体系,与环境绝热隔离,且还需借助于一定的外力作用。本文还简述了热力学3个定律在负温度体系中的延拓和完善。在大学化学各分科的教学课程中,温度是个被广泛使用的物理量,温度越高,体系的能量也越高,反之亦然,且温度始终都为正值。在物理化学教学中,当讨论到激光化学时,温度的符号遇到了困惑。由于激光具有很好的单色性、方向性、高强度,在化学反应中具有良好的选择性,被广泛用于同位素的分离、合成化学、分子裁剪和反应历程的研究等。产生激光技术的关键在于必须使受激发射占优势,即首先使处于高能级E2的粒子数N2远远超过处于低能级E1的粒子数N1。要使原来的Boltzmann平衡分布时低能级上粒子数大于高能级上粒子数的状态反转过来,成为反转分布,这一过程由激光器完成。依据Boltzmann分布公式:N2/N1=exp(-ε/kT)(1)式中ε=hν=E2-E1>0,在粒子反转分布时N2/N1>1,此时温度的符号遇到了困惑,要使式(1)成立,温度T只能取负值。再说温度本身就是与温标有关的相对值,取负值也未尝不可。本文就这一问题,探讨对温度这一既普通又特殊的物理量的认识。1对温度的认识温度这一物理量在自然科学中有着广泛而重要的地位,然而不同的学科分支冠以温度的含义又有不同的说法。热力学认为:任一热力学均相体系在平衡态时存在一个状态函数称为温度,对于一切互呈热平衡的均相体系其温度相等。因而温度是反映热力学体系之间热平衡的物理量,是体系的内在属性,状态函数,但又与其他状态函数不一样,如压力p、体积V。p和V是有绝对值的且又是可以测量的,而温度没有绝对值,它的相对值与温标的选择有关。曾用过的温标有①经验温标,如1709年的华氏温标,1742年的摄氏温标,工程上用的兰金温标。②理想气体温标。③热力学温标,用卡诺循环定义为:61Q1Q2=T1T2(2)④国际实用温标。上述3个温标的温度基准值是1954年国际计量大会确定的水的三相点温度为正数273.16K。按上述规定,温度T总是正的,其最小值为0。分子运动论认为温度标志着物体内部分子无规则运动的剧烈程度,该剧烈程度可定量地用分子的平均平动能Et表示:Et=32kT(3)式中Et为大量分子的平均平动能,具有统计意义。因而温度也只用于大量分子集合体。对于单个分子而言温度是没有意义的。由于平动能都是正的,所以温度也是正的。统计热力学认为:对于一个能量有上限的体系,温度是可以出现负值的,正如前面一个实例所述。2负热力学温度的理论意义前面所述温标是人为规定的,而在热力学中的温度的意义可以从基本关系式得到。对于一个封闭均相组成不变的热力学体系,根据热力学基本关系式:dU=TdS-pdV-δWf和dH=TdS+Vdp-δWf得到1T=(5S5U)V,δWf=0(421)1T=(5S5H)p,δWf=0(422)由(4)式可见,热力学温度的正与负取决于熵S和内能U(或S与H)的变化率的正与负。对于通常的热力学体系,熵总是内能(或焓)的单调上升函数,所以热力学温度T总是正的。这是由于在一般体系中能级是无穷多的。体系的内能越大,就将有更多的粒子去填入更高的能级,体系的微观状态数就越多,熵也越大,因此(5S/5U)V>0,从而T>0。但如果在特殊情况下出现体系的熵值随内能的增加而减小,那就得到一个负温度的状态。这在体系的能级有限时是可能实现的,例如在原子核自旋体系中。现设一个简化了的例子:某一具有N个近独粒子,仅有2个非简并的能级E1和E2的体系。在T=0K时,热激发为0,体系达平衡时能量为极小值,N个粒子均处在低能级E1上,体系的能量为U=NE1。依据Boltzmann分布N2/N1=exp[-(E2-E1)/kT)]=0,此时体系处于完全有序状态,微观状态数Ω→1,熵S=klnΩ→0。若将体系逐步升温直至T→∞,则N2/N1=1,说明有一半的粒子从低能级跃上高能级,此时体系的内能U=N2(E1+E2),热力学几率最大Ωmax=N!/πNi!=N!/N2!N2!,熵值也达到最大值Smax。若使用特殊手段(如激光器)用足够大的能量使产生反转分布,甚至使N个粒子全部位于高能级上...