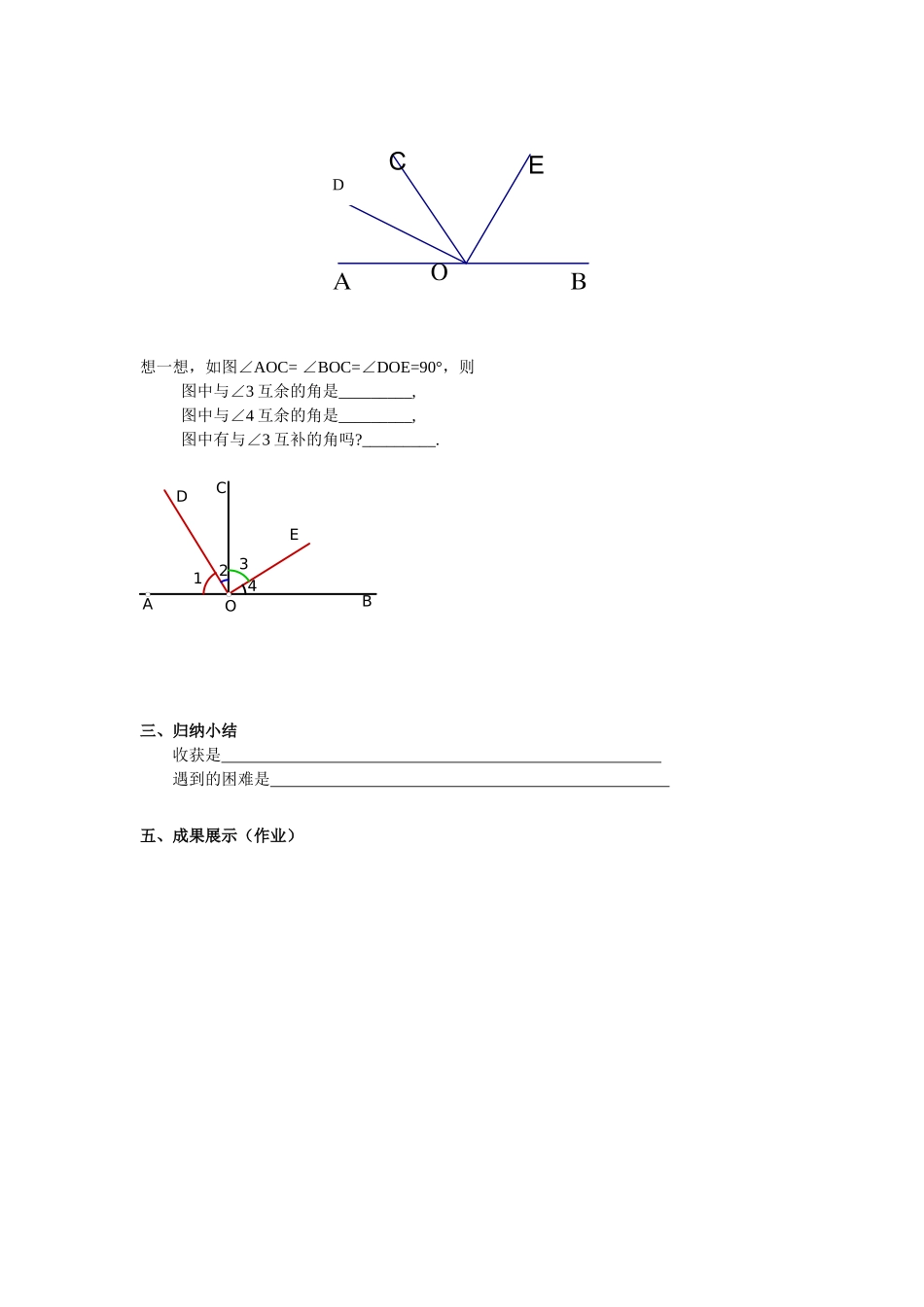
806546442510170120100150801030604.3.3余角和补角(1)学习目标1、在具体的现实情境中,认识一个角的余角和补角,掌握余角和补角的性质。2、进一步提高抽象概括能力,发展空间观念和知识运用能力,学会简单的逻辑推理,并能对问题的结论进行合理的猜想。3、体会观察、归纳、推理对数学知识中获取数学猜想和论证的重要作用,初步体会数学中推理的严谨性和结论的确定性,能在独立思考和小组交流中获益。学习重点:认识角的互余、互补关系及其性质,确定方位是本节课的重点。学习难点:通过简单的推理,归纳出余角、补角的性质,并能用规范的语言描述性质是难点。学习方法:探究、归纳与练习相结合学习过程:一、探索新知:1、结合教材理解互为余角的定义:如果两个角的和是90°(直角),那么这两个角叫做互为余角,其中一个角是另一个角的余角。即:∠1是∠2的余角或∠2是∠1的余角。2、理解应用⑴:图中给出的各角,那些互为余角?3、结合教材理解互为补角的定义:如果两个角的和是180°(平角),那么这两个角叫做互为补角,其中一个角是另一个角的补角。即:∠3是∠4的补角或∠4是∠3的补角。4、理解应用⑵:(1)图中给出的各角,那些互为补角?(2)填下列表:∠a∠a的余角∠a的补角80°45°79°39′x°结论:同一个锐角的补角比它的余角大(3)填空:①70°的余角是,补角是。②∠a(∠a<90°)的它的余角是,它的补角是。重要提醒:ⅰ如何表示一个角的余角和补角锐角∠a的余角是(90°—∠a)∠a的补角是(180°—∠a)ⅱ互余和互补是两个角的数量关系,与它们的位置无关。1、90度的角叫余角,180度的角叫补角。()3、如果一个角有补角,那么这个角一定是钝角。(4、互补的两个角不可能相等。5、钝角没有余角,但一定有补角。()6、互余的两个角一定都是锐角,两个锐角一定互余.()()二、尝试应用例1:若一个角的补角等于它的余角4倍,求这个角的度数。练习:P1393、4一个角的余角比这个角的补角的还小10°,求这个角例2已知,点A,O,B在同一直线上,OD,OE分别为∠AOC和∠BOC的角平分线,找图中互余和互补的角。22、()3.互为余角2,1,则,9032107、果。()B互余.A与那么,)(90B,A00xx2、7、想一想,如图∠AOC=∠BOC=∠DOE=90°,则图中与∠3互余的角是_________,图中与∠4互余的角是_________,图中有与∠3互补的角吗?_________.BCDE1234OA三、归纳小结收获是遇到的困难是五、成果展示(作业)ECD