第九章 真空中的静电场VIP免费

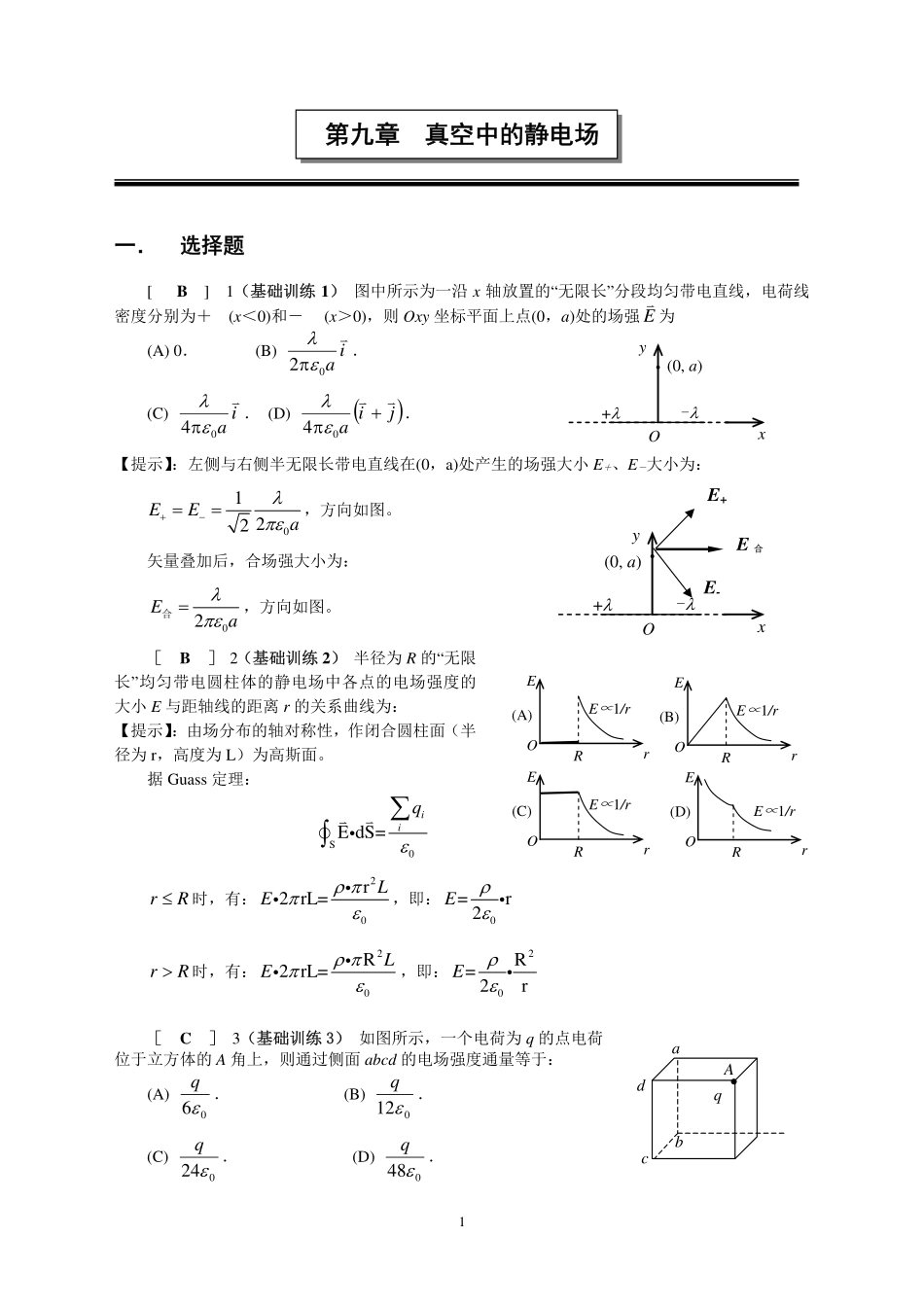
1第九章真空中的静电场一．选择题[B]1（基础训练1）图中所示为一沿x轴放置的“无限长”分段均匀带电直线，电荷线密度分别为＋(x＜0)和－(x＞0)，则Oxy坐标平面上点(0，a)处的场强E为(A)0．(B)ia02．(C)ia04．(D)jia04．【提示】：左侧与右侧半无限长带电直线在(0，a)处产生的场强大小E＋、E－大小为：0122EEa，方向如图。矢量叠加后，合场强大小为：02Ea合，方向如图。［B］2（基础训练2）半径为R的“无限长”均匀带电圆柱体的静电场中各点的电场强度的大小E与距轴线的距离r的关系曲线为：【提示】：由场分布的轴对称性，作闭合圆柱面（半径为r，高度为L）为高斯面。据Guass定理：S0EdS=iiqrR时，有：20r2rL=LE，即：0=r2ErR时，有：20R2rL=LE，即：20R=2rE［C］3（基础训练3）如图所示，一个电荷为q的点电荷位于立方体的A角上，则通过侧面abcd的电场强度通量等于：(A)06q．(B)012q．(C)024q．(D)048q．AbcdaqE+E-E合O+-xy(0,a)O+-xy(0,a)EOr(C)E∝1/rREOr(A)E∝1/rREOr(B)E∝1/rREOr(D)E∝1/rR2【提示】：添加7个与如图相同的小立方体构成一个大立方体，使A处于大立方体的中心。则大立方体外围的六个正方形构成一个闭合的高斯面。由Gauss定理知，通过该高斯面的电通量为0q。再据对称性可知，通过侧面abcd的电场强度通量等于024q。［D］4（基础训练6）在点电荷+q的电场中，若取图中P点处为电势零点，则M点的电势为(A)aq04．(B)aq08．(C)aq04．(D)aq08．【提示】：220048PaMMaqqVEdldrra［B］5（自测提高6）如图所示，两个同心的均匀带电球面，内球面半径为R1、带电荷Q1，外球面半径为R2、带有电荷Q2．设无穷远处为电势零点，则在内球面之内、距离球心为r处的P点的电势U为：(A)rQQ0214．(B)20210144RQRQ．(C)0．(D)1014RQ．【提示】：根据带点球面在求内外激发电势的规律，以及电势叠加原理即可知结果。［D］6（自测提高8）8、点电荷-q位于圆心O处，A、B、C、D为同一圆周上的四点，如图9-38示。现将一试验电荷从A点分别移动到B、C、D各点，则(A)从A到B，电场力作功最大。(B)从A到C，电场力作功最大。(C)从A到D，电场力作功最大。(D)从A到各点，电场力作功相等。【提示】：根据电场力做功与电势差之间的关系式：0()PQPQAqVV，以及A、B、C、D四点电势相等即可知结果。［C］7（自测提高10）如图所示，在真空中半径分别为R和2R的两个同心球面，其上分别均匀地带有电荷+q和－3q．今将一电荷为+Ｑ的带电粒子从内球面处由静止释放，则该粒子到达外球面时的动能为：(A)RQq04．(B)RQq02．(C)08QqR．(D)RQq083．【提示】：静电力做功()ABABQUQVV等于动能的增加。其中：00034428AqqqVRRR；0003242428BqqqVRRRABVV、为内球面、外球面的电势，代上即得结果。aa+qPM-3q＋qQR2RQ2Q1OPrR2R1ABDCO-q图9-383二．填空题1（基础训练9）已知空气的击穿场强为30kV/cm，空气中一带电球壳直径为1m，以无限远处为电势零点，则这球壳能达到的最高电势是1.5106V__。【提示】：带电球壳的电势：04QVR；球壳表面场强为：2004QER。联立两式知：VER。2（基础训练13）两个平行的“无限大”均匀带电平面，其电荷面密度分别为＋和＋2，如图所示，则A、B、C三个区域的电场强度分别为：EA＝032，EB＝02，EC＝032(设方向向右为正)．【提示】：A、B、C三个区域的场强，为两“无限大”均匀带电平面在该区域独自产生场强的矢量叠加。3（基础训练17）AC为一根长为2l的带电细棒，左半部均匀带有负电荷，右半部均匀带有正电荷。电荷线密度分别为－和＋，如图所示。O点在棒的延长线上，距A端的距离为l．P点在棒的垂直平分线上，到棒的垂直距离为l．以棒的中点B为电势的零点。则O点电势Uo＝43ln40；P点电势Up＝___0___．【提示】：题中棒的中点B为电势的零点与远处为电势的零点...