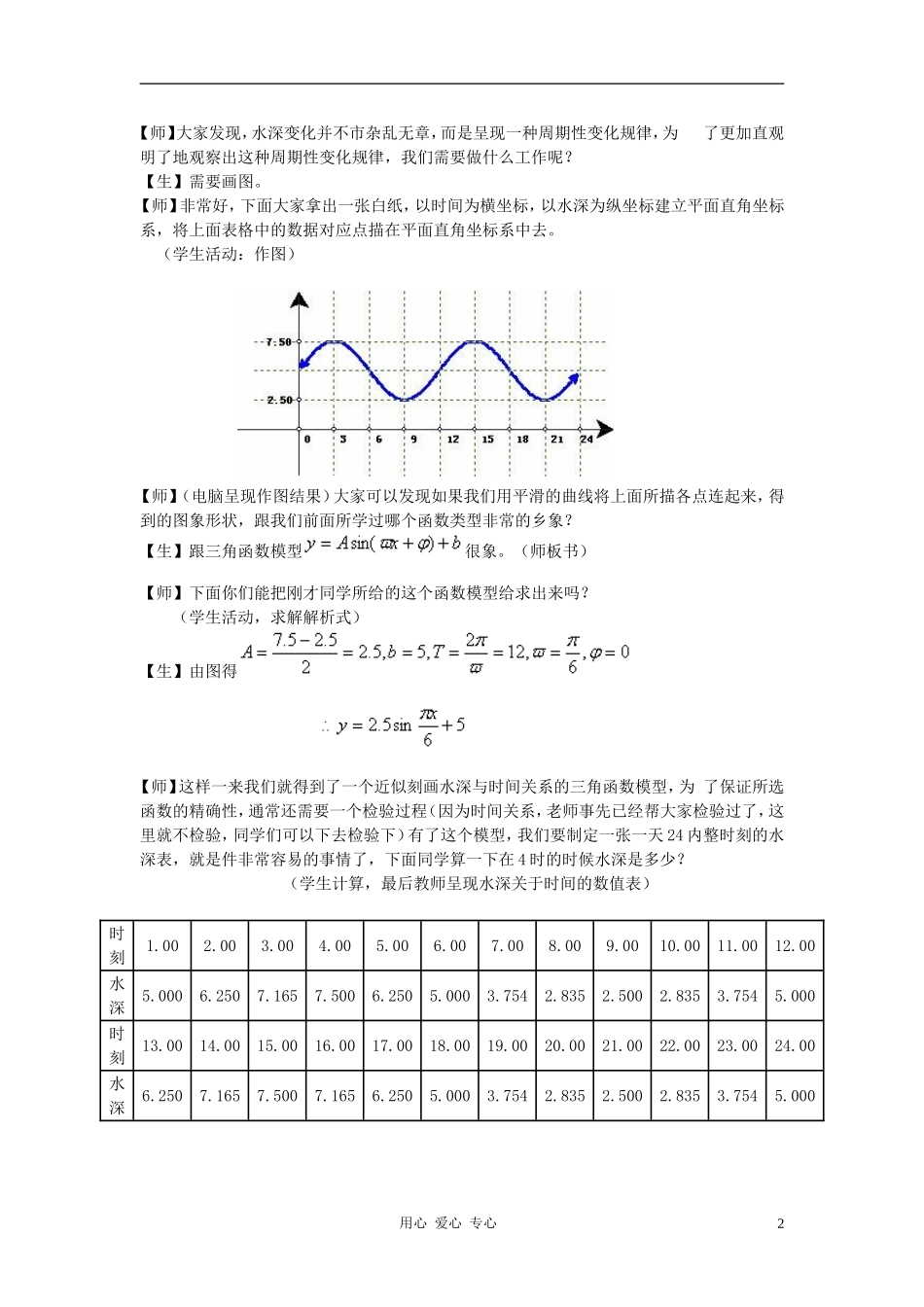
三角函数模型的简单应用---潮汐问题教学目标:巩固已知三角函数,求给定自变量对应的函数值;已知三角函数值,求相应自变量的值;利用图象解三角不等式;利用二分法求相应方程的近似解;培养学生数学应用意识;提高学生利用信息技术处理一些实际计算的能力。教学重点:用三角函数模型刻画潮汐变化规律,用函数思想解决具有周期变化的实际问题。教学难点:对问题实际意义的数学解释,从实际问题中抽象出三角函数模型。教学媒体:几何画板教学流程:教学过程:1.情景展示,新课导入【师】经过前面的学习,大家知道,在客观现实世界中存在着大量的周期性变化现象,而要定量地去刻画这些现象,我们通常需要借助于三角函数这一重要数学模型。这节课我们将来学习三角函数模型的简单应用。(教师板书课题:§1.6三角函数模型的简单应用)2.问题提出,探究解决【师】老师想问大家一个问题:若干年后,如果在座的各位有机会当上船长的话,当你的船只要到某个港口去,你作为船长,你希望知道关于那个港口的一些什么情况?【生】水深情况。【师】是的,我们要到一个陌生的港口时,是非常想得到一张有关那个港口的水深与时间的对应关系数值表。那么这张表格是如何产生的呢?请同学们看下面这个问题。问题探究1:如图所示,下面是某个码头在某年某个季节每天的时间与水深的关系表:时间0.001.003.006.008.009.0012.0015.0018.0021.0024.00水深5.06.257.55.02.842.55.07.55.02.55.0【师】请同学们仔细观察表格中的数据,你能够从中得到一些什么信息?【生】(思考中)发现水深的最大值是7.5米,最小值是2.5米。【师】水的深度变化有什么特点吗?【生】水的深度开始由5.0米增加到7.5米,后逐渐减少一直减少到2.5,又开始逐渐变深,增加到7.5米后,又开始减少。用心爱心专心1【师】大家发现,水深变化并不市杂乱无章,而是呈现一种周期性变化规律,为了更加直观明了地观察出这种周期性变化规律,我们需要做什么工作呢?【生】需要画图。【师】非常好,下面大家拿出一张白纸,以时间为横坐标,以水深为纵坐标建立平面直角坐标系,将上面表格中的数据对应点描在平面直角坐标系中去。(学生活动:作图)【师】(电脑呈现作图结果)大家可以发现如果我们用平滑的曲线将上面所描各点连起来,得到的图象形状,跟我们前面所学过哪个函数类型非常的乡象?【生】跟三角函数模型很象。(师板书)【师】下面你们能把刚才同学所给的这个函数模型给求出来吗?(学生活动,求解解析式)【生】由图得【师】这样一来我们就得到了一个近似刻画水深与时间关系的三角函数模型,为了保证所选函数的精确性,通常还需要一个检验过程(因为时间关系,老师事先已经帮大家检验过了,这里就不检验,同学们可以下去检验下)有了这个模型,我们要制定一张一天24内整时刻的水深表,就是件非常容易的事情了,下面同学算一下在4时的时候水深是多少?(学生计算,最后教师呈现水深关于时间的数值表)时刻1.002.003.004.005.006.007.008.009.0010.0011.0012.00水深5.0006.2507.1657.5006.2505.0003.7542.8352.5002.8353.7545.000时刻13.0014.0015.0016.0017.0018.0019.0020.0021.0022.0023.0024.00水深6.2507.1657.5007.1656.2505.0003.7542.8352.5002.8353.7545.000用心爱心专心2【师】有了水深关于时间的函数模型以后,作为船长考虑的问题还没有结束,因为船只在进出港时,每艘船只的吃水深度是不一样,下面我们就看一看把这两方面的情况都考虑进去的一个问题:问题探究2:一艘货船的吃水深度(船底与水面的距离)为4米,安全条例规定至少要有1.5米的安全间隙(船底与洋底的距离),试问:该船何时能够进入港口?在港口能呆多久?【师】货船能够进入港口所需要满足的条件是什么?(师生一起分析)【师】只有当“实际水深吃水深度+安全间隙”时,船只才可以进去或离开港口。怎样用数学语言将这一条件给转述出来呢?【生】,即,(师生齐分析)解三角不等式,通常我们是算去边界值,然后再确定解的范围。【师】令(学生活动:操作计算器计算),【师】我们知道三角方程在实数范围内有解就有无数个,那么在[0,24]范围内,其他一些解该怎么...