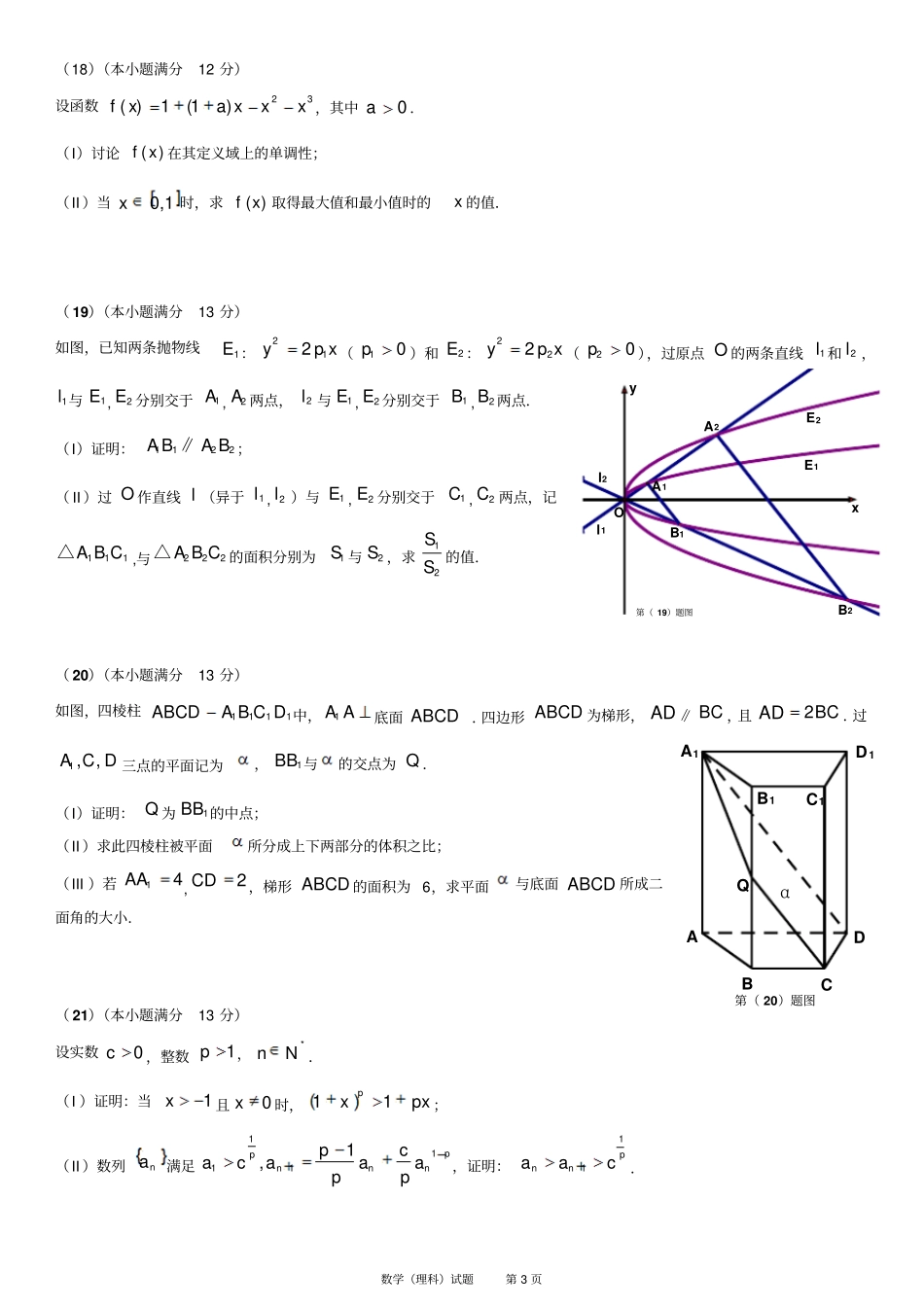
数学(理科)试题第1页2014年普通高等学校招生全国统一考试(安徽卷)数学(理科)第Ⅰ卷(选择题共50分)一.选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)设i是虚数单位,z表示复数z的共轭复数.若iz1,则ziz1()A.-2B.-2iC.2D.2i(2)“0x”是“0)1ln(x”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件(3)如图所示,程序框图(算法流程图)的输出结果是()A.34B.55C.78D.89(4)以平面直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位.已知直线l的参数方程是31yytx(t为参数),圆C的极坐标方程是cos4,则直线l被圆C截得的弦长为()A.14B.142C.2D.22(5)x,y满足约束条件02202202yxyxyx,若axyz取得最大值的最优解不唯一,则实数a的值为()A.21或-1B.2或21C.2或1D.2或-1(6)设函数)(xf(Rx)满足xxfxfsin)()(.当x0时,0)(xf,则)623(f()A.21B.23C.0D.21(7)一个多面体的三视图如图所示,则该多面体的表面积为().A.21+3B.18+3C.21D.18(8)从正方体六个面的对角线中任取两条作为一对,其中所成的角为60°的共有()对.A.24B.30C.48D.60(9)若函数axxxf21)(的最小值为3,则实数a的值为()A.5或8B.-1或5C.-1或-4D.-4或8(10)在平面直角坐标系xoy中,已知向量a,b,1ba,0ba,点Q满足)(2baOQ.曲线20,sincosbaOPPC丨,区域RrRPQrP,丨0.若C为两段分离的曲线,则()A.31RrB.Rr31C.31RrD.Rr31数学(理科)试题第2页第(13)题图OA1A212134yx第II卷(非选择题共100分)二.填空题:本大题共5小题,每小题5分,共25分.(11)若将函数)42sin()(xxf的图像向右平移个单位,所得图像关于y轴对称,则的最小正值是.(12)数列na是等差数列,若11a,33a,55a构成公比为q的等比数列,则q=.(13)设0a,n是大于1的自然数,nax1的展开式为nnxaxaxaa22210.若点),(iiaiA(2,1,0i)的位置如图所示,则a=.(14)设21,FF分别是椭圆E:1222byx(10b)的左、右焦点,过点1F的直线交椭圆E与A,B两点,若xAFBFAF211,3轴,则椭圆E的方程为.(15)已知两个不相等的非零向量a,b,两组向量54321,,,,xxxxx和54321,,,,yyyyy均由2个a和3个b排列而成.记5544332211yxyxyxyxyxS,minS表示S所有可能取值中的最小值.则下列正确的命题的是(写出所有正确命题的编号).①S有5个不同的值;②若a⊥b,则minS与a无关;③若a∥b,则minS与b无关;④若b>a4,则minS>0;⑤若b=a4,minS=28a,则a与b的夹角为4三.解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.解答写在答题卡上的指定区域内.(16)(本小题满分12分)设△ABC的内角CBA,,对边的长分别是a,b,c,且3b,1c,BA2.(I)求a的值:(II)求)4sin(A的值.(17)(本小题满分12分)甲乙两人进行围棋比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛,假设每局甲获胜的概率为32,乙获胜的概率为31,各局比赛结果互相独立.(I)求甲在4局以内(含4局)赢得比赛的概率;(II)记X为比赛决出胜负时的总局数,求X的分布列和均值(数学期望).数学(理科)试题第3页第(20)题图αQDABA1D1C1B1Cl2l1E2E1第(19)题图B2A2OA1yxB1(18)(本小题满分12分)设函数32)1(1)(xxxaxf,其中0a.(I)讨论)(xf在其定义域上的单调性;(II)当1,0x时,求)(xf取得最大值和最小值时的x的值.(19)(本小题满分13分)如图,已知两条抛物线1E:xpy122(01p)和2E:xpy222(02p),过原点O的两条直线1l和2l,1l与1E,2E分别交于1A,2A两点,2l与1E,2E分别交于1B,2B两点.(I)证明:2211BABA∥;(II)过O作直线l(异于1l,2l)与1E,2E分别交于1C,2C两点,记111CBA△,与222CBA△的面积分别为1S与2S,求21SS的值.(20)(本小题满分13分)如图,四棱柱1111DCBAABCD中,AA1底面ABCD.四边形ABCD为梯形,AD∥BC,且ADBC2.过DCA,,1三点的平面记为,1BB与的交点为Q.(I)证明:Q为1BB的中点;(II)求此四棱柱被平...