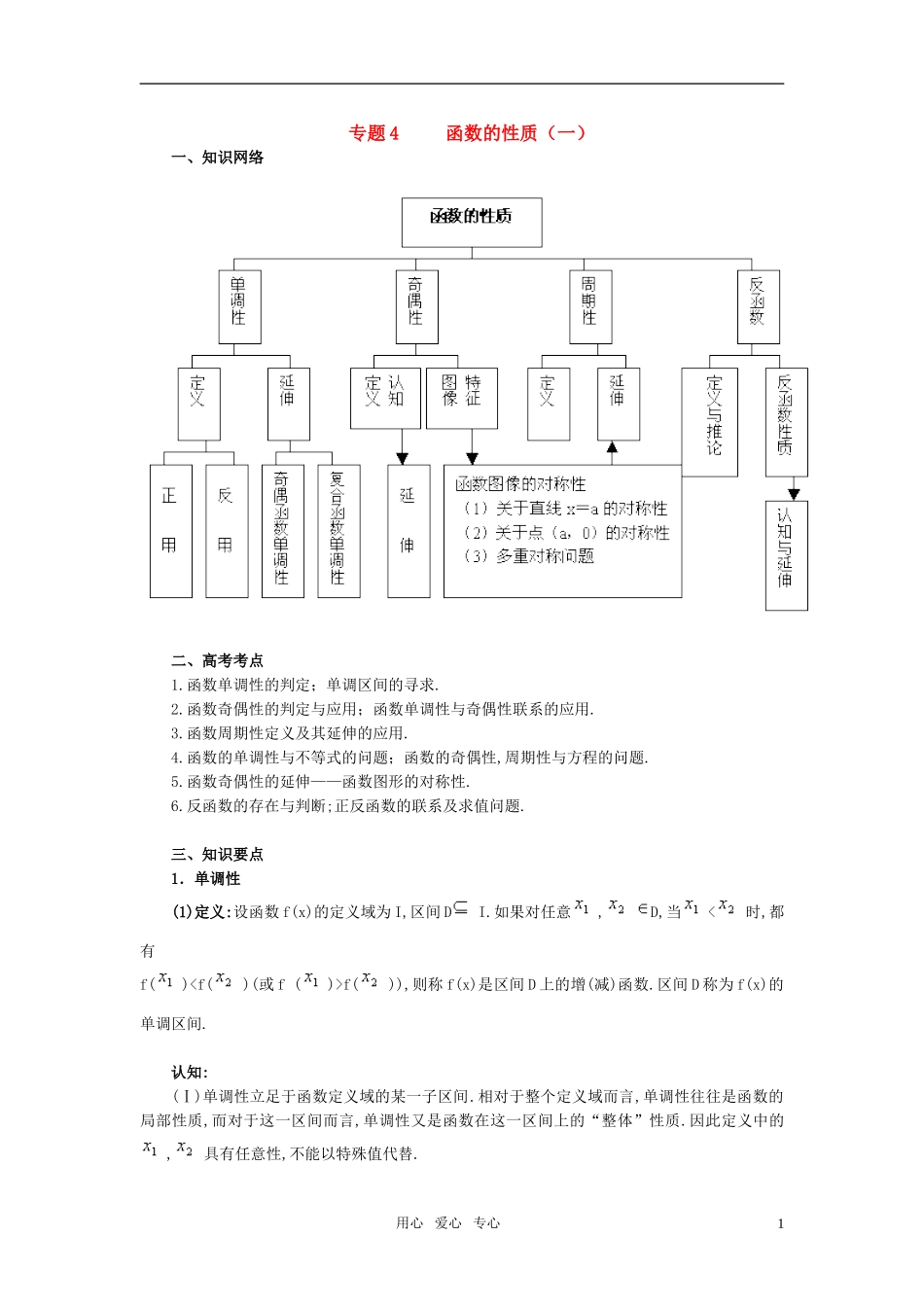
专题4函数的性质(一)一、知识网络二、高考考点1.函数单调性的判定;单调区间的寻求.2.函数奇偶性的判定与应用;函数单调性与奇偶性联系的应用.3.函数周期性定义及其延伸的应用.4.函数的单调性与不等式的问题;函数的奇偶性,周期性与方程的问题.5.函数奇偶性的延伸——函数图形的对称性.6.反函数的存在与判断;正反函数的联系及求值问题.三、知识要点1.单调性(1)定义:设函数f(x)的定义域为I,区间DI.如果对任意,D,当<时,都有f()f()),则称f(x)是区间D上的增(减)函数.区间D称为f(x)的单调区间.认知:(Ⅰ)单调性立足于函数定义域的某一子区间.相对于整个定义域而言,单调性往往是函数的局部性质,而对于这一区间而言,单调性又是函数在这一区间上的“整体”性质.因此定义中的,具有任意性,不能以特殊值代替.用心爱心专心1(Ⅱ)函数f(x)在区间D上递增(或递减),与f(x)图像在区间D上部分(从左向右)的上升(或下降)是一样的.(Ⅲ)注意到定义均为充要性命题,因此,在函数的单调性之下,自变量的不等关系与相应函数值间的不等关系相互贯通:f(x)在D上为增函数且f(),,D.(2)定义的应用单调性的定义,是判断,证明函数的单调性以及寻求函数单调区间的基本依据.应用函数的单调性定义的解题三部曲为(Ⅰ)设值定大小:设,为给定区间上任意两个自变量值,且<;(Ⅱ)作差并变形:作差f()-f(),并将差式向着有利于判断差式符号的方向变形;(Ⅲ)定号作结论:确定差值的符号,当符号不确定时考虑分类讨论,而后根据定义作出结论.在这里,差式的变形到位与否是解题成功的关键环节,差式变形的主要手段有通分,分解因式,配方以及有理化分母(或分子)等,其中,应用最为广泛的是分解因式.(3)延伸单调性相同的两个函数的复合函数必为增函数;单调性相反的两个函数的复合函数必为减函数.复合函数单调性问题的解题思路(Ⅰ)引元分解:引入新元,将所给函数分解为两个(或两个以上)简单函数(化整为零);(Ⅱ)分别考察:分别考察内,外两层函数在各自定义域上的单调性;(Ⅲ)综合结论:利用单调性定义或上述命题,由内,外两层函数的单调性作出相关结论.2.奇偶性(1)定义:如果对于函数f(x)的定义域内的任意一个x,都有f(-x)=-f(x),则称f(x)为这一定义域内的奇函数;如果对于函数f(x)的定义域内的任意一个x,都有f(-x)=f(x),则称f(x)为这一定义域内的偶函数.(2)认知:(Ⅰ)上述定义要求一对实数x,-x必须同时都在f(x)的定义域内,注意到实数x,-x在x轴上的对应点关于原点对称(或与原点重合),故知f(x)的定义域关于原点对称是f(x)具有奇偶性的必要条件.(Ⅱ)判断函数奇偶性的步骤:用心爱心专心2①考察函数定义域;②考察f(-x)与f(x)的关系;③根据定义作出判断.(Ⅲ)定义中条件的等价转化①f(-x)=-f(x)f(x)+f(-x)=0;或f(-x)=-f(x)=-1(f(x)≠0)②f(-x)=f(x)f(x)-f(-x)=0;或f(-x)=f(x)=1(f(x)≠0)(3)延伸:(Ⅰ)设函数f(x)是定义域关于原点对称的任意一个函数,则有f(x)=+=g(x)+p(x)其中,g(x)=为偶函数,p(x)=为奇函数.即对于定义域关于原点对称的任何一个函数f(x),f(x)总可以表示为一个奇函数与一个偶函数的和.(Ⅱ)若f(x)为奇函数且零属于f(x)的定义域,则f(0)=0.(4)奇(偶)函数图像的特征(Ⅰ)奇函数图像关于原点对称;(Ⅱ)偶函数图像关于y轴对称.(5)奇偶性与单调性的联系当函数f(x)既具奇偶性,又在某区间上单调时,我们可利用奇、偶函数的定义导出以下命题:设G,G'为函数f(x)的定义域的子区间,并且区间G与G'关于原点对称,则有(Ⅰ)当f(x)为奇函数时,f(x)在区间G和区间G'上的单调性相同;(Ⅱ)当f(x)为偶函数时,f(x)在区间G和区间G'上的单调性相反.这一命题又可凝练为八个字:区间对称,奇同偶反.四.经典例题例1.讨论函数f(x)=ax+(x>0)的单调性,其中a>0,且b>0.分析1.运用函数的单调性定义.设0<<,则用心爱心专心3f()-f()=a(-)(尽量简化分母)由此可见,差式的符号取决于的符号,因此,以确定的符号为主旨展开讨论.在这里,当划分区间的分界点难以确定时,可考虑运用极端分析法,即从极端情形入手分析与寻觅:令=且=0,解得==于是考虑以这些零值为分界点划分所给区间(0,+∞).解法1.设,(0,+∞)且<,...