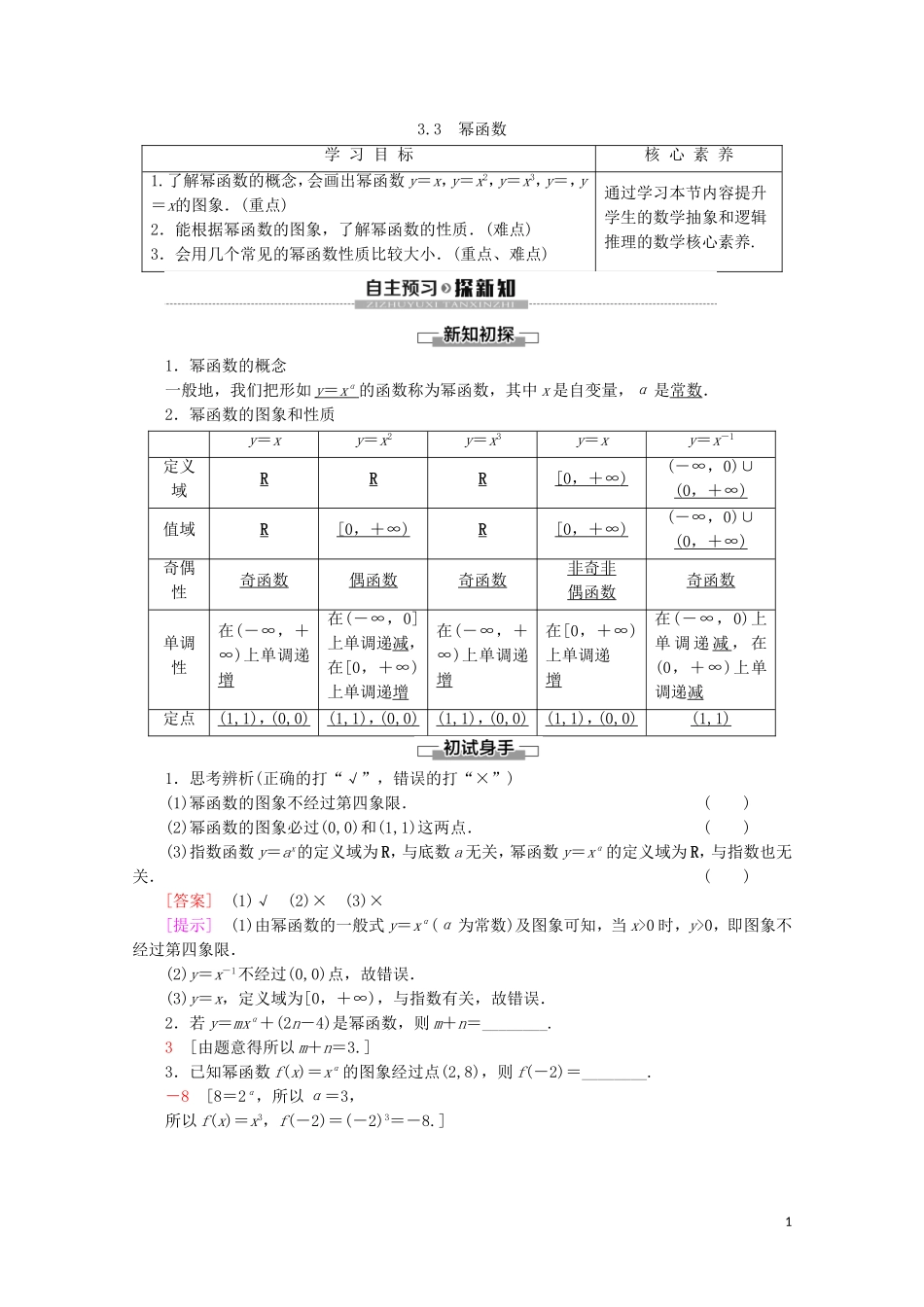
3.3幂函数学习目标核心素养1.了解幂函数的概念,会画出幂函数y=x,y=x2,y=x3,y=,y=x的图象.(重点)2.能根据幂函数的图象,了解幂函数的性质.(难点)3.会用几个常见的幂函数性质比较大小.(重点、难点)通过学习本节内容提升学生的数学抽象和逻辑推理的数学核心素养.1.幂函数的概念一般地,我们把形如y=xα的函数称为幂函数,其中x是自变量,α是常数.2.幂函数的图象和性质y=xy=x2y=x3y=xy=x-1定义域RRR[0,+∞)(-∞,0)∪(0,+∞)值域R[0,+∞)R[0,+∞)(-∞,0)∪(0,+∞)奇偶性奇函数偶函数奇函数非奇非偶函数奇函数单调性在(-∞,+∞)上单调递增在(-∞,0]上单调递减,在[0,+∞)上单调递增在(-∞,+∞)上单调递增在[0,+∞)上单调递增在(-∞,0)上单调递减,在(0,+∞)上单调递减定点(1,1),(0,0)(1,1),(0,0)(1,1),(0,0)(1,1),(0,0)(1,1)1.思考辨析(正确的打“√”,错误的打“×”)(1)幂函数的图象不经过第四象限.()(2)幂函数的图象必过(0,0)和(1,1)这两点.()(3)指数函数y=ax的定义域为R,与底数a无关,幂函数y=xα的定义域为R,与指数也无关.()[答案](1)√(2)×(3)×[提示](1)由幂函数的一般式y=xα(α为常数)及图象可知,当x>0时,y>0,即图象不经过第四象限.(2)y=x-1不经过(0,0)点,故错误.(3)y=x,定义域为[0,+∞),与指数有关,故错误.2.若y=mxα+(2n-4)是幂函数,则m+n=________.3[由题意得所以m+n=3.]3.已知幂函数f(x)=xα的图象经过点(2,8),则f(-2)=________.-8[8=2α,所以α=3,所以f(x)=x3,f(-2)=(-2)3=-8.]1幂函数的概念【例1】已知y=(m2+2m-2)x+2n-3是幂函数,求m,n的值.思路点拨:由幂函数的定义列式求解.[解]由题意得解得∴m=-3,n=为所求.1.幂函数y=xα要满足三个特征(1)幂xα前系数为1;(2)底数只能是自变量x,指数是常数;(3)项数只有一项.2.求幂函数解析式时常用待定系数法,即设解析式为f(x)=xα,根据条件求出α.1.下列函数是幂函数的有________.(填序号)①y=x2x;②y=2x2;③y=x;④y=x2+1;⑤y=-;⑥y=x.③⑥[根据幂函数的定义,只有③⑥符合题意.]2.已知幂函数f(x)=xα的图象经过,则f(100)=________.[由题知2α==2,∴α=-.∴f(x)=x,∴f(100)=100==.]比较大小【例2】比较下列各组数中两个数的大小:(1)与;(2)与;(3)0.25与6.25;(4)0.20.6与0.30.4.思路点拨:可以借助幂函数的单调性或中间量进行比较.[解](1) y=x是[0,+∞)上的增函数,且>,∴>.(2) y=x-1是(-∞,0)上的减函数,且-<-,∴>.(3)0.25==2,6.25=2.5. y=x是[0,+∞)上的增函数,且2<2.5,∴2<2.5,即0.25<6.25.(4)由幂函数的单调性,知0.20.6<0.30.6,又y=0.3x是减函数,∴0.30.4>0.30.6,从而20.20.6<0.30.4.比较幂值的大小,关键在于构造适当的函数:(1)若指数相同而底数不同,则构造幂函数;(2)若指数不同而底数相同,则构造指数函数;(3)若指数与底数都不同,需考虑是否能把指数或底数化为相同,是否可以引入中间量.3.比较下列各组中两个数的大小:(1)3,3.1;(2)a1.5,(a+1)1.5(a>0);(3)(-0.88),(-0.89).[解](1)因为函数y=x在(0,+∞)内是减函数,所以3>3.1.(2)函数y=x1.5在(0,+∞)内是增函数,又a>0,a+1>a,所以(a+1)1.5>a1.5.(3)函数y=x在R上为增函数,所以(-0.88)>(-0.89).幂函数的图象与性质[探究问题]1.做幂函数y=x的图象应该怎么做?[提示]①因为0<<1,故函数y=x在第一象限内是单调递增的,并且在(0,1)上应在y=x的上方,在(1,+∞)上应在y=x的下方.②函数的定义域为R,且为偶函数,故将y轴右侧的图象关于y轴对称到y轴左侧,即得到y=x的图象(略).2.从上述过程能否归纳出作幂函数y=xα的图象的步骤?[提示]①先看α,按α<0,0<α<1,α>1来分类(α=0,α=1两种特殊情况可直接作图),并确定在第一象限的图象的形状.②再看定义域以及函数的奇偶性,结合奇偶性利用图象变换得到函数在y轴左侧的图象.3.作出y=x的图象(草图),并说明若x>y时,x,y与0的大小关系有多少种?[提示]y=x在第一象限...