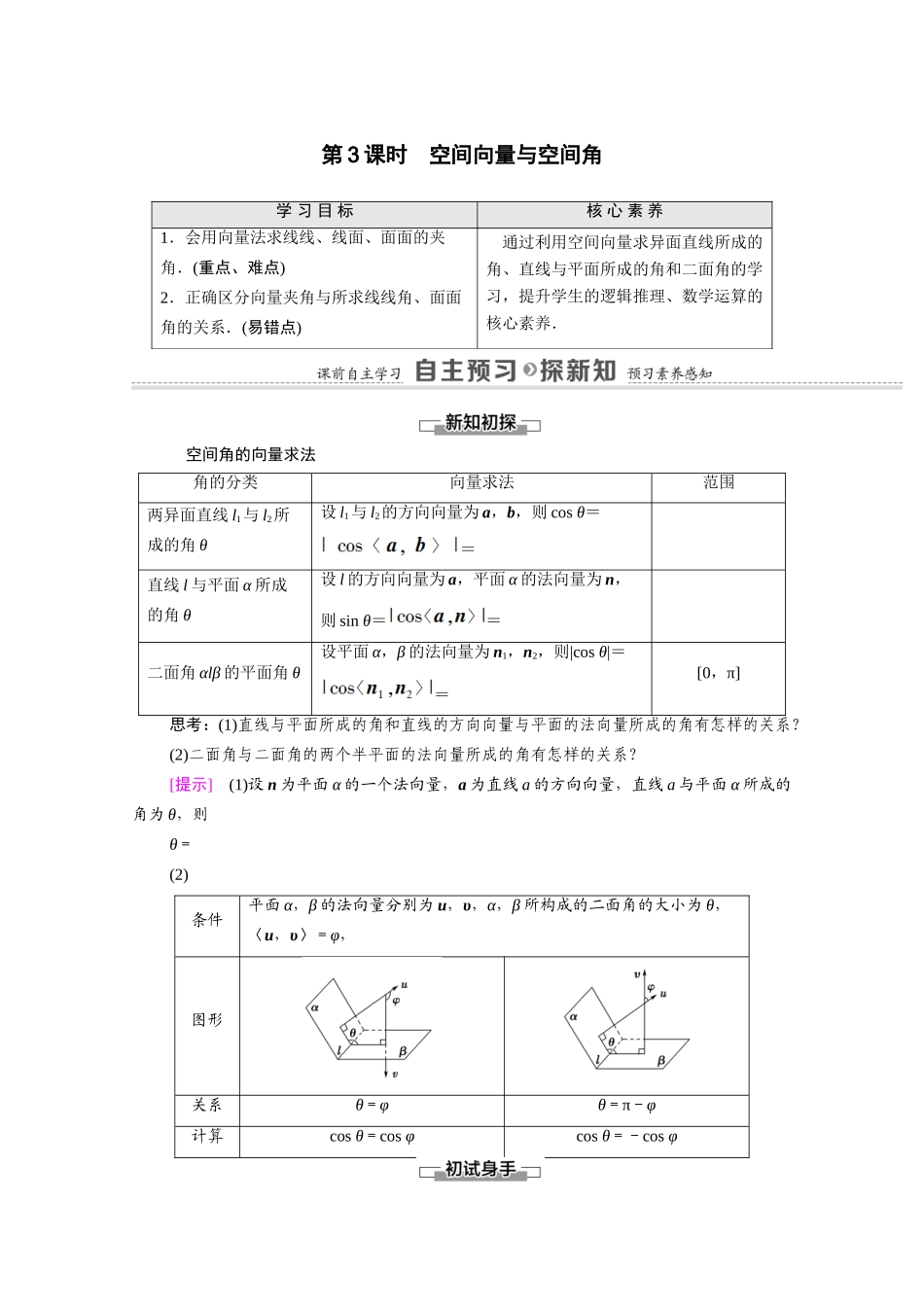
第3课时空间向量与空间角学习目标核心素养1.会用向量法求线线、线面、面面的夹角.(重点、难点)2.正确区分向量夹角与所求线线角、面面角的关系.(易错点)通过利用空间向量求异面直线所成的角、直线与平面所成的角和二面角的学习,提升学生的逻辑推理、数学运算的核心素养.空间角的向量求法角的分类向量求法范围两异面直线l1与l2所成的角θ设l1与l2的方向向量为a,b,则cosθ==直线l与平面α所成的角θ设l的方向向量为a,平面α的法向量为n,则sinθ==二面角αlβ的平面角θ设平面α,β的法向量为n1,n2,则|cosθ|==[0,π]思考:(1)直线与平面所成的角和直线的方向向量与平面的法向量所成的角有怎样的关系?(2)二面角与二面角的两个半平面的法向量所成的角有怎样的关系?[提示](1)设n为平面α的一个法向量,a为直线a的方向向量,直线a与平面α所成的角为θ,则θ=(2)条件平面α,β的法向量分别为u,υ,α,β所构成的二面角的大小为θ,〈u,υ〉=φ,图形关系θ=φθ=π-φ计算cosθ=cosφcosθ=-cosφ1.如图所示,在正方体ABCDA1B1C1D1中,M,N,P分别是棱CC1,BC,A1B1上的点,若∠B1MN=90°,则∠PMN的大小是()A.等于90°B.小于90°C.大于90°D.不确定A[A1B1⊥平面BCC1B1,故A1B1⊥MN,则MP·MN=(MB1+B1P)·MN=MB1·MN+B1P·MN=0,∴MP⊥MN,即∠PMN=90°.]2.已知二面角αlβ等于θ,异面直线a,b满足a⊂α,b⊂β,且a⊥l,b⊥l,则a,b所成的角等于()A.θB.π-θC.-θD.θ或π-θD[应考虑0≤θ≤与<θ≤π两种情况.]3.已知向量m,n分别是直线l与平面α的方向向量、法向量,若cos〈m,n〉=-,则l与α所成的角为()A.30°B.60°C.150°D.120°B[设l与α所成的角为θ,则sinθ=|cos〈m,n〉|=,∴θ=60°,应选B.]4.正方体ABCDA′B′C′D′中,M,N分别是棱BB′和B′C′的中点,则异面直线MN与AD所成角的大小为________.45°[以DA,DC,DD′为正交基底建立空间直角坐标系Oxyz,设正方体棱长为1,则A(1,0,0),M,N,∴AD=(-1,0,0),MN=. cos〈MN,AD〉===,∴〈MN,AD〉=45°,即MN和AD所成角的大小为45°.]求两条异面直线所成的角【例1】如图,在三棱柱OABO1A1B1中,平面OBB1O1⊥平面OAB,∠O1OB=60°,∠AOB=90°,且OB=OO1=2,OA=,求异面直线A1B与AO1所成角的余弦值的大小.[解]建立如图所示的空间直角坐标系,则O(0,0,0),O1(0,1,),A(,0,0),A1(,1,),B(0,2,0),∴A1B=(-,1,-),O1A=(,-1,-).∴|cos〈A1B,O1A〉===.∴异面直线A1B与AO1所成角的余弦值为.1.几何法求异面直线的夹角时,需要通过作平行线将异面直线的夹角转化为平面角,再解三角形来求解,过程相当复杂;用向量法求异面直线的夹角,可以避免复杂的几何作图和论证过程,只需对相应向量进行运算即可.2.由于两异面直线夹角θ的范围是,而两向量夹角α的范围是[0,π],故应有cosθ=|cosα|,求解时要特别注意.[跟进训练]1.如图所示,在平行六面体ABCDA1B1C1D1中,平面ABCD与平面D1C1CD垂直,且∠D1DC=,DC=DD1=2,DA=,∠ADC=,求异面直线A1C与AD1所成角的余弦值.[解]建立如图所示的空间直角坐标系,则A(,0,0),D1(0,1,),C(0,2,0),D(0,0,0),由AA1=DD1得A1(,1,).因为A1C=DC-DA1=(-,1,-),D1A=DA-DD1=(,-1,-).所以cos〈A1C,D1A〉===-.所以异面直线A1C与AD1所成角的余弦值为.求直线与平面所成的角【例2】如图,四棱锥PABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.(1)证明MN∥平面PAB;(2)求直线AN与平面PMN所成角的正弦值.思路探究:(1)线面平行的判定定理⇒MN∥平面PAB.(2)利用空间向量计算平面PMN与AN方向向量的夹角⇒直线AN与平面PMN所成角的正弦值.[解](1)证明:由已知得AM=AD=2.如图,取BP的中点T,连接AT,TN,由N为PC的中点知TN∥BC,TN=BC=2.又AD∥BC,故TN綊AM,所以四边形AMNT为平行四边形,于是MN∥AT.因为AT⊂平面PAB,MN⊄平面PAB,所以MN∥平面PAB.(2)如图,取BC的中点E,连接AE.由AB=AC...