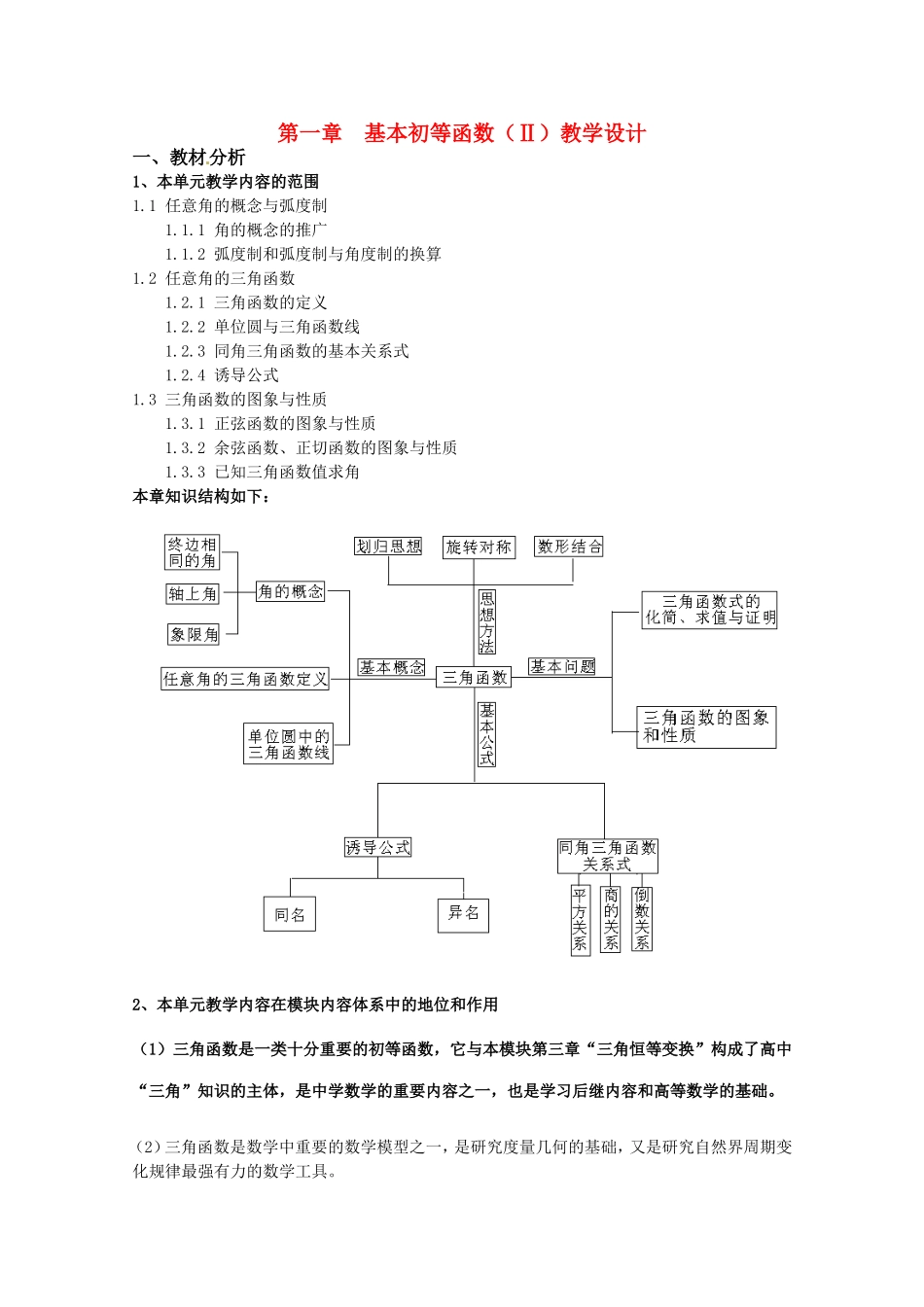
第一章基本初等函数(Ⅱ)教学设计一、教材分析1、本单元教学内容的范围1.1任意角的概念与弧度制1.1.1角的概念的推广1.1.2弧度制和弧度制与角度制的换算1.2任意角的三角函数1.2.1三角函数的定义1.2.2单位圆与三角函数线1.2.3同角三角函数的基本关系式1.2.4诱导公式1.3三角函数的图象与性质1.3.1正弦函数的图象与性质1.3.2余弦函数、正切函数的图象与性质1.3.3已知三角函数值求角本章知识结构如下:2、本单元教学内容在模块内容体系中的地位和作用(1)三角函数是一类十分重要的初等函数,它与本模块第三章“三角恒等变换”构成了高中“三角”知识的主体,是中学数学的重要内容之一,也是学习后继内容和高等数学的基础。(2)三角函数是数学中重要的数学模型之一,是研究度量几何的基础,又是研究自然界周期变化规律最强有力的数学工具。(3)三角函数作为描述周期现象的重要数学模型,与其它学科如天文学、物理学等联系非常紧密。因此三角函数的学习可以培养学生的数学应用能力。(4)三角函数的基础知识,主要是平面几何中的相似形和圆。研究三角函数的方法,主要是在必修1中建立的研究初等函数的方法。因此,通过对三角函数的学习,可以初步地把“数”与“形”联系起来。(5)通过对三角函数的学习,不仅能使学生获得新的知识和技能,而且可以培养学生的辨证唯物主义观点,提高分析问题和解决问题的能力。3、本单元教学内容总体教学目标[来源:学科网](1)任意角的概念、弧度制了解任意角的概念.了解弧度制的概念,能进行弧度与角度的互化.(2)任意角的三角函数理解任意角的正弦、余弦、正切的定义;了解任意角的余切、正割、余割的定义;并会利用单位圆中的有向线段表示正弦、余弦和正切,并理解其原理。理解同角三角函数的基本关系式:22sincos1xx,sintancosxxx;借助单位圆的直观性探索正弦、余弦、正切的诱导公式,能进行同角三角函数之间的变换,会求任意角的三角函数值,并记住某些特殊角的三角函数值。(3)三角函数的图像和性质能结合三角函数的图象或单位圆理解正弦函数、余弦函数和正切函数的性质,特别要深入领会三角函数的周期性与最小正周期的意义。能正确使用“五点法”、“几何法”、“图象变换法”画出正弦函数、余弦函数和)sin(xAy的图象,能正确地作出正切函数的简图,结合具体实例,了解)sin(xAy的实际意义,了解)sin(xAy中的参数对函数图象变化的影响以及它们的物理意义,会用变换法说明有关函数图象间的关系。会用三角函数解决简单的实际问题,了解三角函数是描述周期变化现象的重要模型,领会它在描述自然界周期现象中的作用。会由已知三角函数值求角[来源:学_科_网]4、本单元教学内容重点和难点分析本单元教学内容的重点:任意角三角函数的概念,同角三角函数的关系式,诱导公式,正弦函数的性质与图象,函数)sin(xAy的图象和正弦函数图象间的关系。本单元教学内容的难点:(1)弧度制概念的建立一方面,学生已经熟悉并掌握了角度制,因此,在学习弧度制时,会对学习弧度制的必要性产生怀疑,因而缺乏积极性;另一方面,由于弧度制的定义方法比较特殊,表面上看不出这种定义的优越性,因而对这种更加抽象、更加不易理解的新的度量制容易产生畏难心理。在教学中应注意解决学生学习心理上的障碍。(2)周期函数的概念三角函数是学生在中学阶段学习的各类函数中唯一具有周期性的函数,而函数的周期性,由于数学刻画比较抽象,逻辑上比较严谨,所以较难理解。在教学中应遵循从具体到抽象,由简单到复杂,从理解到应用的原则,逐步引入这个概念,加深对这个性质的理解。(3)正弦型函数)sin(xAy的图象变换由于变换过程较长,变化较多,所以学生不易掌握。在教学时可以采取先分解,再综合,化整为零,逐个突破,然后再统一归纳的方法。最终,使学生能对变换的根据有全面而深刻的了解,明白不论是图象的平移还是图象的伸缩,)sin(xAy中的,都是针对x而言的,达到真正掌握的目的。(4)综合运用公式进行求值、化简、证明在这里,教学难点主要表现为:如何培养学生根据题目的不同特点,选择适当的公...