高中数学 第三章 指数函数和对数函数 3.5 对数函数 3.5.2 对数函数的图像与性质（1）教案1 北师大版必修1-北师大版高一必修1数学教案VIP免费

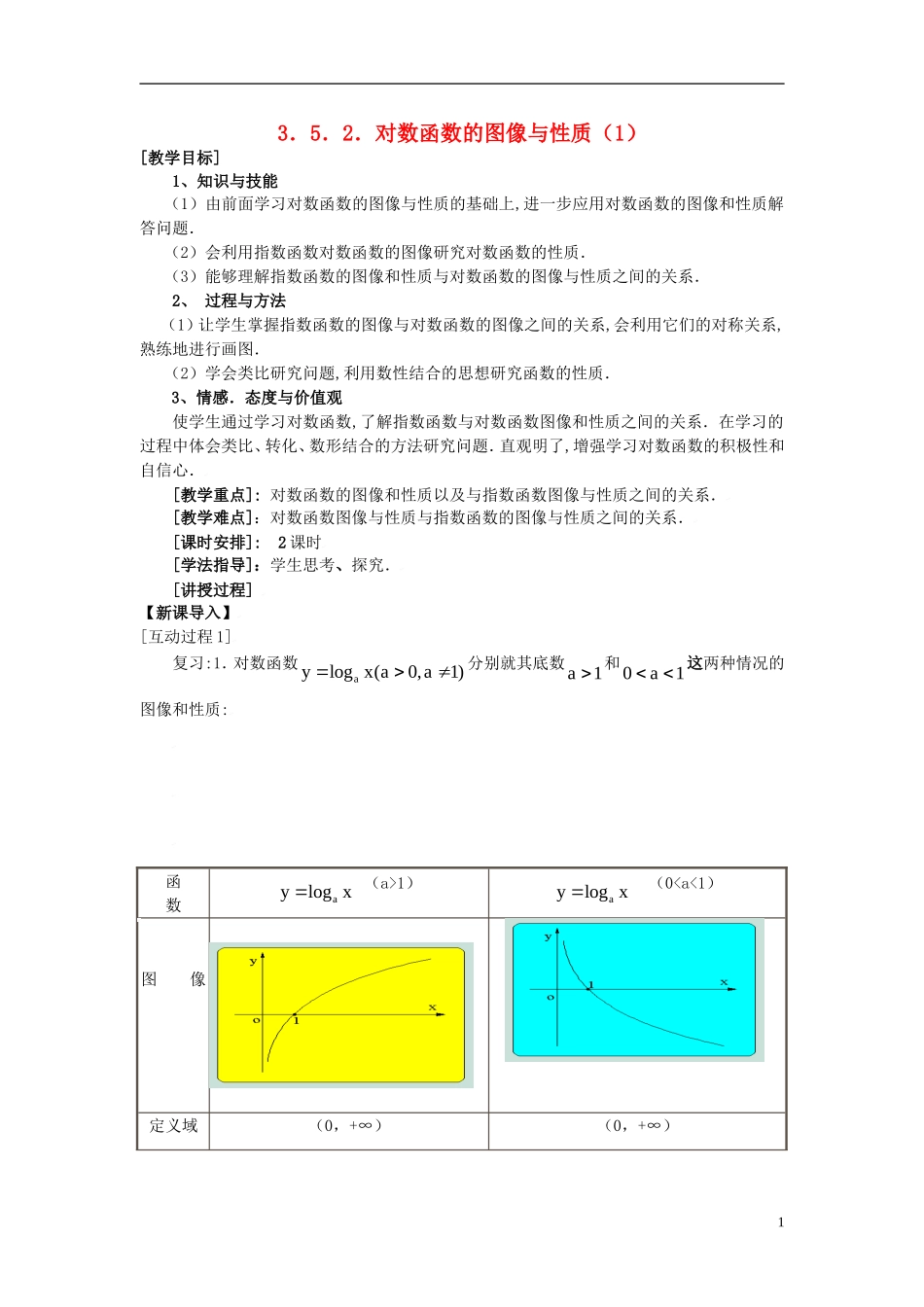
3．5．2．对数函数的图像与性质（1）[教学目标]1、知识与技能（1）由前面学习对数函数的图像与性质的基础上,进一步应用对数函数的图像和性质解答问题．（2）会利用指数函数对数函数的图像研究对数函数的性质．（3）能够理解指数函数的图像和性质与对数函数的图像与性质之间的关系．2、过程与方法（1）让学生掌握指数函数的图像与对数函数的图像之间的关系,会利用它们的对称关系,熟练地进行画图．（2）学会类比研究问题,利用数性结合的思想研究函数的性质．3、情感．态度与价值观使学生通过学习对数函数,了解指数函数与对数函数图像和性质之间的关系．在学习的过程中体会类比、转化、数形结合的方法研究问题．直观明了,增强学习对数函数的积极性和自信心．[教学重点]:对数函数的图像和性质以及与指数函数图像与性质之间的关系．[教学难点]：对数函数图像与性质与指数函数的图像与性质之间的关系．[课时安排]:2课时[学法指导]：学生思考、探究．[讲授过程]【新课导入】[互动过程1]复习:1．对数函数aylogx(a0,a1)分别就其底数a1和0a1这两种情况的图像和性质:函数aylogx（a>1）aylogx（0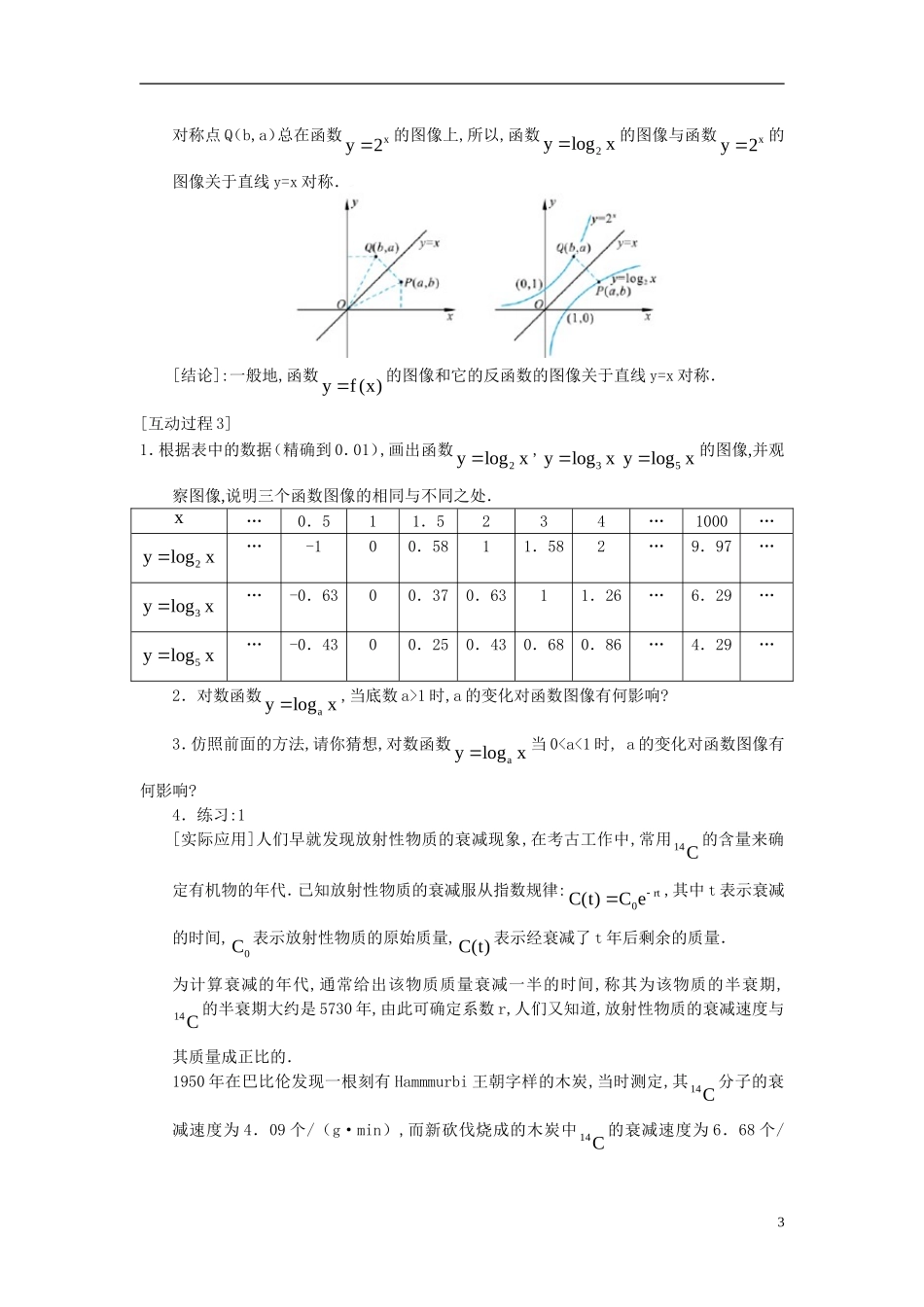1时，y>000x>1时，y<0练习:1．在同一直角坐标系中画出下列函数的图像211323(1)ylogx;(2)ylogx;(3)ylogx;(4)ylogx;(5)ylgx2．求下列函数的定义域:31(1)ylogx2;(2)yln4x解:（1）因为x20,即x2,所以函数3ylogx2的定义域为{x|x2};（2）因为104x,即x4,所以函数1yln4x的定义域为{x|x4}3．比较下列各题中两个数的大小:(1)lg0.3,lg0.4;0.50.5(2)log3,log0.23(3)loge,ln3;aa(4)log0.9,log1.2(a0,a1)解:（1）因为10>1,函数ylgx是增函数,0．3<0．4,所以lg0.3lg0.4;（2）因为0．5<1,函数0.5ylogx是减函数,3>0．2,所以0.50.5log3log0.2;（3）因为函数3ylogx是增函数,e3,所以33logelog31,同理1lneln3,所以3logeln3;（4）当a1时,函数aylogx在(0,)上是增函数,此时,aalog0.9log1.2,当0a1时,函数aylogx在(0,)上是减函数,此时,aalog0.9log1.2[互动过程2]观察在同一坐标系内函数2ylogx与函数xy2的图像，分析它们之间的关系．解:从图上可以看出点P（a,b）与点Q（b,a）关于直线y=x对称,函数2ylogx与函数xy2互为反函数,对应于函数2ylogx图像上任意一点P（a,b）,P关于直线y=x的2对称点Q（b,a）总在函数xy2的图像上,所以,函数2ylogx的图像与函数xy2的图像关于直线y=x对称．[结论]:一般地,函数yf(x)的图像和它的反函数的图像关于直线y=x对称．[互动过程3]1．根据表中的数据（精确到0．01）,画出函数2ylogx,3ylogx5ylogx的图像,并观察图像,说明三个函数图像的相同与不同之处．x…0．511．5234…1000…2ylogx…-100．5811．582…9．97…3ylogx…-0．6300．370．6311．26…6．29…5ylogx…-0．4300．250．430．680．86…4．29…2．对数函数aylogx,当底数a>1时,a的变化对函数图像有何影响?3．仿照前面的方法,请你猜想,对数函数aylogx当0