高中数学 第三节 数学算法及算法的三种基本逻辑结构教案 新人教B版VIP免费

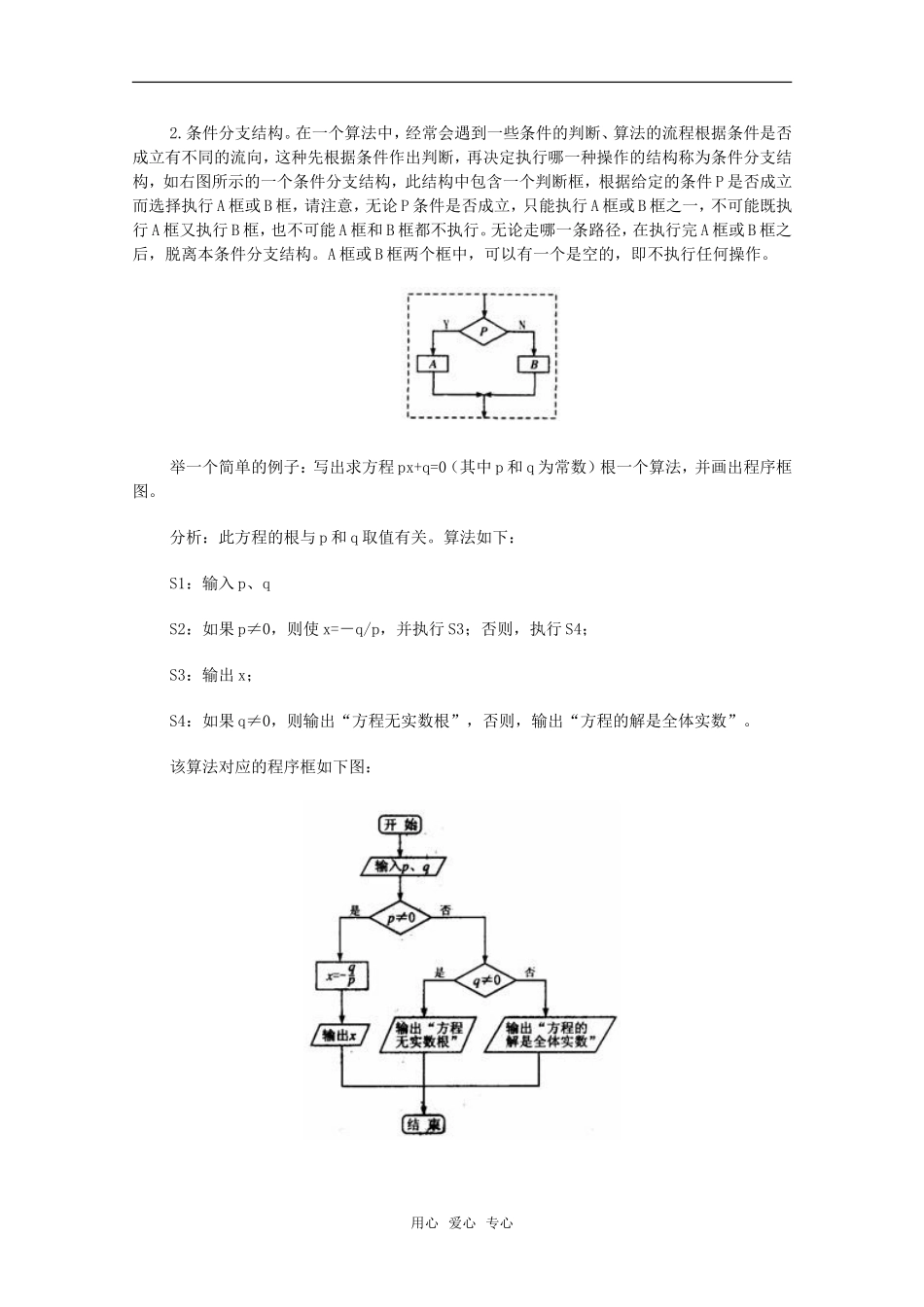
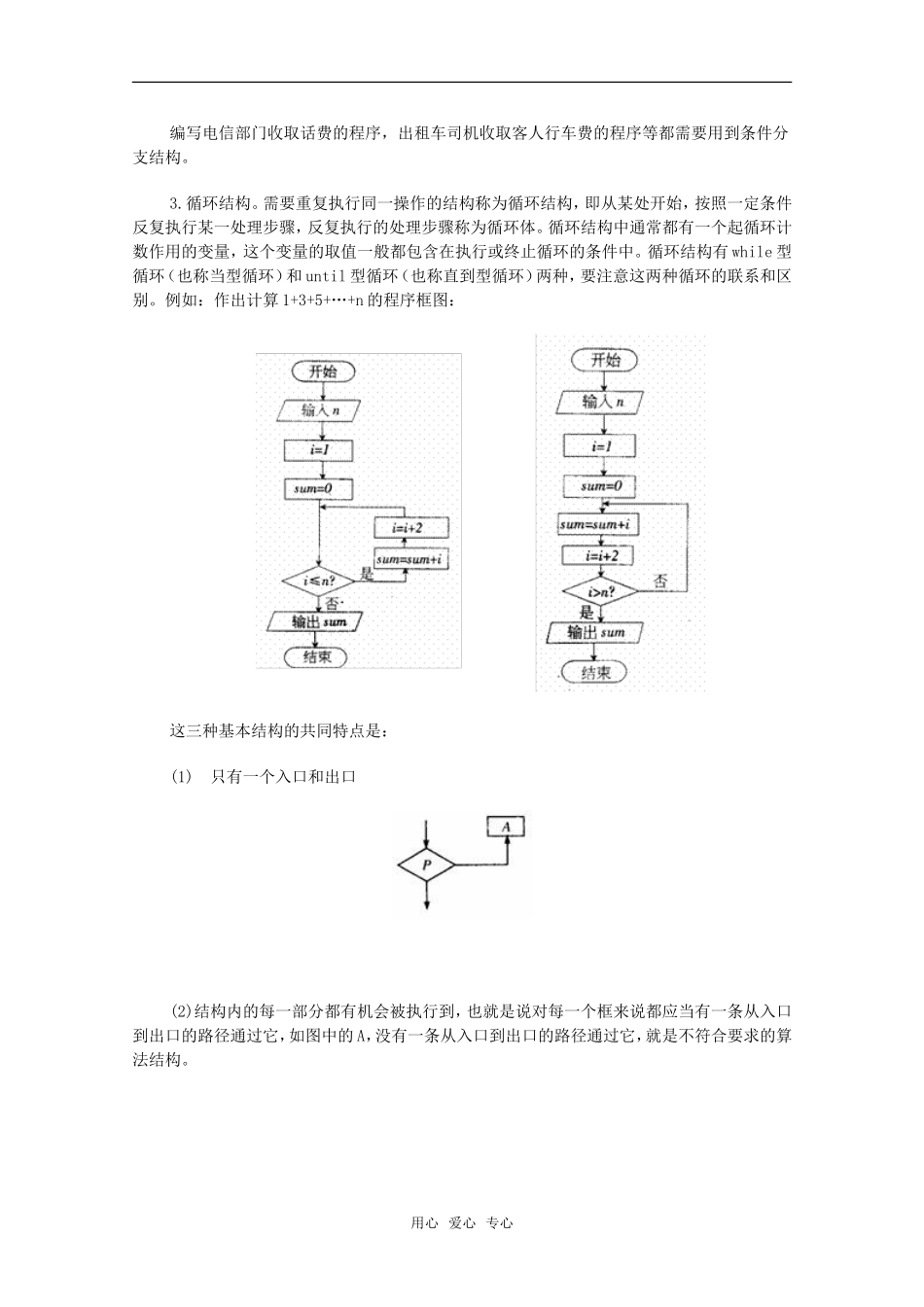
高中数学算法及算法的三种基本逻辑结构算法是数学及其应用的重要组成部分，是计算数学的重要基础。随着现代信息技术的飞速发展，算法在科学技术、社会发展中发挥着越来越大的作用，并日益融入社会生活的各个方面。所谓算法是指在有限步骤内求解某类问题所使用的一组定义明确的规则。需要特别指出的是，我国古代数学中蕴含了丰富的数学思想，比如二分法、秦九韶算法、割圆术、求两个数的最大公约数等。算法重在用一个统一的方法有步骤地解决一类问题，但它不是唯一的，一个好的算法应该用较少的便于实现的步骤去有效的解决问题。把算法引入高中数学教学，有利于培养学生的逻辑思维能力，概括问题能力，养成良好的思维和学习习惯，必将对高中数学教学产生深远影响。一般算法有顺序结构、条件分支结构、循环结构三种基本逻辑结构。1.顺序结构。顺序结构是最简单的算法结构，语句与语句之间，框与框之间是按从上到下的顺序进行的。它是由若干个依次执行的处理步骤组成的，它也是任何一个算法都离不开的一种算法结构，如图，其中A和B两个框是依次执行的，只有在执行完A框所指定的操作后，才能接着执行B框所指定的操作。顺序结构的一个简单的例子是交换变量a和b的值。算法如下：S1：m=a;S2：a=b;S1：b=m.程序框图如图：用心爱心专心2.条件分支结构。在一个算法中，经常会遇到一些条件的判断、算法的流程根据条件是否成立有不同的流向，这种先根据条件作出判断，再决定执行哪一种操作的结构称为条件分支结构，如右图所示的一个条件分支结构，此结构中包含一个判断框，根据给定的条件P是否成立而选择执行A框或B框，请注意，无论P条件是否成立，只能执行A框或B框之一，不可能既执行A框又执行B框，也不可能A框和B框都不执行。无论走哪一条路径，在执行完A框或B框之后，脱离本条件分支结构。A框或B框两个框中，可以有一个是空的，即不执行任何操作。举一个简单的例子：写出求方程px+q=0（其中p和q为常数）根一个算法，并画出程序框图。分析：此方程的根与p和q取值有关。算法如下：S1：输入p、qS2：如果p≠0，则使x=－q/p，并执行S3；否则，执行S4；S3：输出x；S4：如果q≠0，则输出“方程无实数根”，否则，输出“方程的解是全体实数”。该算法对应的程序框如下图：用心爱心专心编写电信部门收取话费的程序，出租车司机收取客人行车费的程序等都需要用到条件分支结构。3.循环结构。需要重复执行同一操作的结构称为循环结构，即从某处开始，按照一定条件反复执行某一处理步骤，反复执行的处理步骤称为循环体。循环结构中通常都有一个起循环计数作用的变量，这个变量的取值一般都包含在执行或终止循环的条件中。循环结构有while型循环（也称当型循环）和until型循环（也称直到型循环）两种，要注意这两种循环的联系和区别。例如：作出计算1+3+5+…+n的程序框图：这三种基本结构的共同特点是：(1)只有一个入口和出口(2)结构内的每一部分都有机会被执行到，也就是说对每一个框来说都应当有一条从入口到出口的路径通过它，如图中的A，没有一条从入口到出口的路径通过它，就是不符合要求的算法结构。用心爱心专心(3)结构内不存在死循环，即无终止的循环，像右图就是一个死循环，在流程图中是不允许死循环出现的。以上是我通过学习和讲授算法一章对算法知识的一点认识，算法的学习还可以渗透到高中数学的各个章节中，比如二分法，错位相减法求和，还贷问题，一元二次不等式解法等。总之，只要多留心，多思考，算法不但并不可怕，还将成为我们数学教学的一个有力的工具。用心爱心专心