高中数学 第二章第01课时映射教师专用教案 新人教A版VIP免费

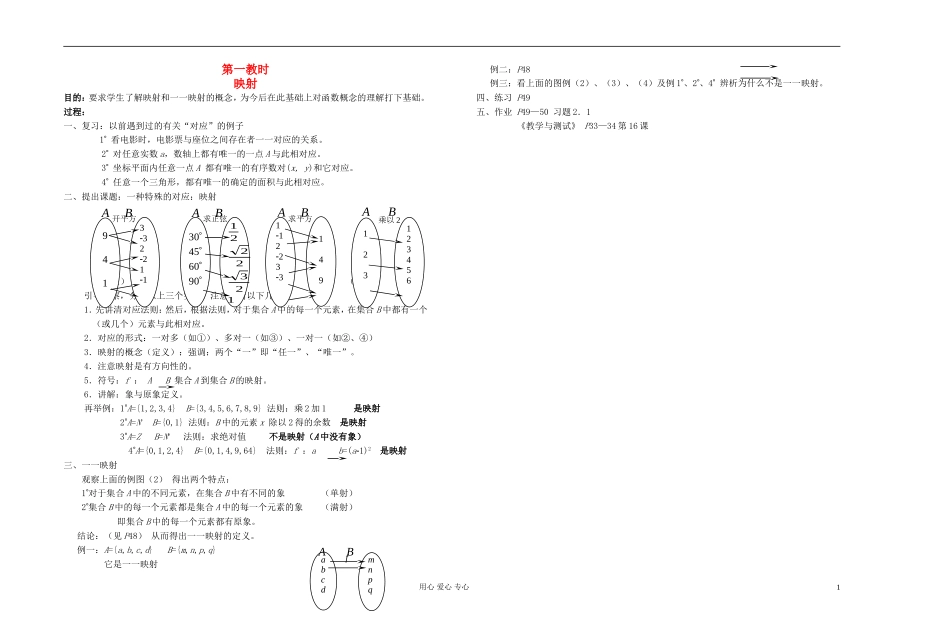
第一教时映射目的：要求学生了解映射和一一映射的概念，为今后在此基础上对函数概念的理解打下基础。过程：一、复习：以前遇到过的有关“对应”的例子1看电影时，电影票与座位之间存在者一一对应的关系。2对任意实数a，数轴上都有唯一的一点A与此相对应。3坐标平面内任意一点A都有唯一的有序数对(x,y)和它对应。4任意一个三角形，都有唯一的确定的面积与此相对应。二、提出课题：一种特殊的对应：映射（1）（2）（3）（4）引导观察，分析以上三个实例。注意讲清以下几点：1．先讲清对应法则：然后，根据法则，对于集合A中的每一个元素，在集合B中都有一个（或几个）元素与此相对应。2．对应的形式：一对多（如①）、多对一（如③）、一对一（如②、④）3．映射的概念（定义）：强调：两个“一”即“任一”、“唯一”。4．注意映射是有方向性的。5．符号：f：AB集合A到集合B的映射。6．讲解：象与原象定义。再举例：1A={1,2,3,4}B={3,4,5,6,7,8,9}法则：乘2加1是映射2A=N+B={0,1}法则：B中的元素x除以2得的余数是映射3A=ZB=N*法则：求绝对值不是映射（A中没有象）4A={0,1,2,4}B={0,1,4,9,64}法则：f：ab=(a1)2是映射三、一一映射观察上面的例图（2）得出两个特点：1对于集合A中的不同元素，在集合B中有不同的象（单射）2集合B中的每一个元素都是集合A中的每一个元素的象（满射）即集合B中的每一个元素都有原象。结论：（见P48）从而得出一一映射的定义。例一：A={a,b,c,d}B={m,n,p,q}它是一一映射例二：P48例三：看上面的图例（2）、（3）、（4）及例1、2、4辨析为什么不是一一映射。四、练习P49五、作业P49—50习题2．1《教学与测试》P33—34第16课用心爱心专心1ABABABAB941332211304560901232221112233149123123456开平方求正弦求平方乘以2abcdmnpqABf