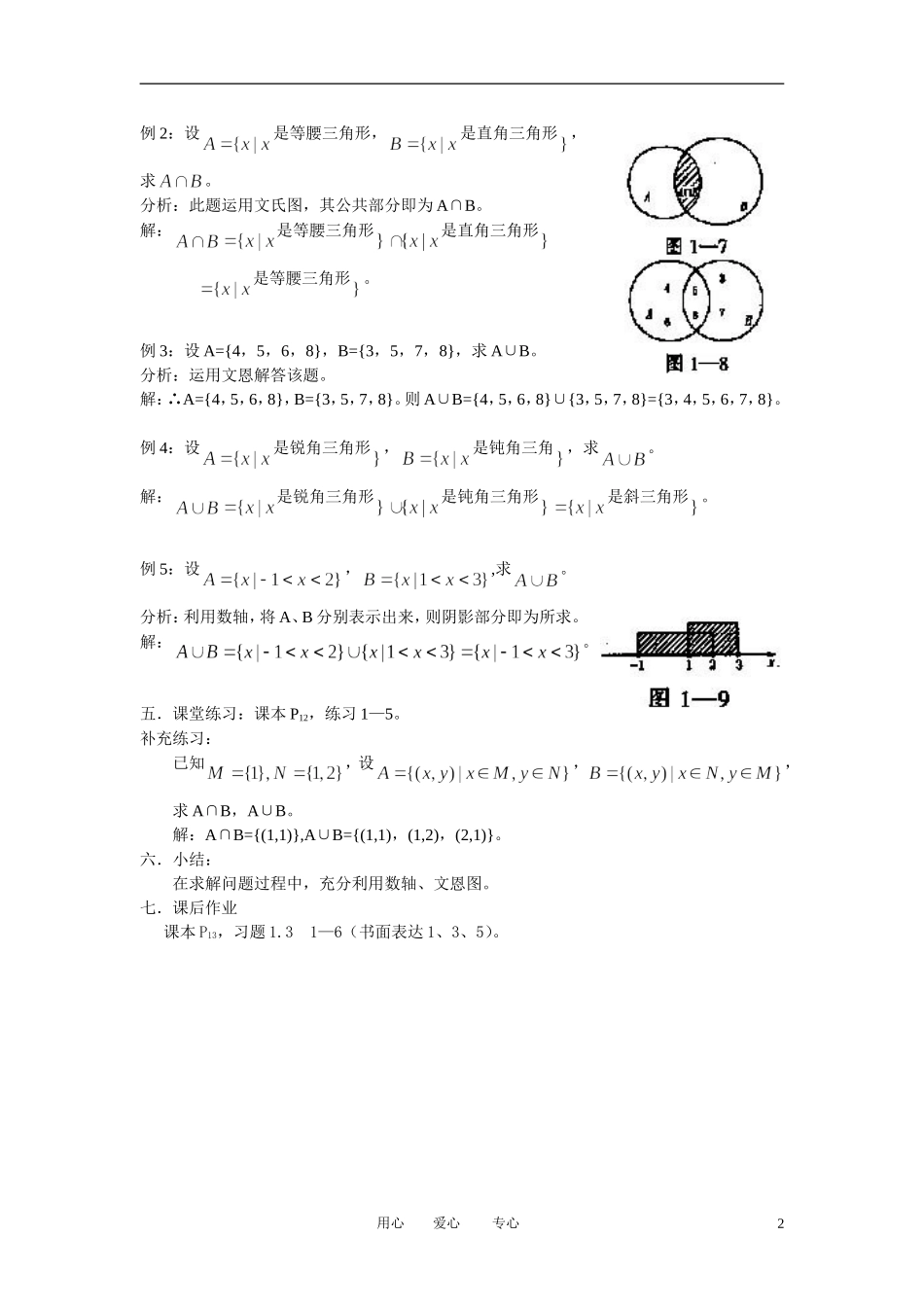
交集与并集(1)一.课题:交集与并集(1)二.教学目标:1。理解交集与并集的概念。2。会求两个已知集合交集、并集。3。认识由具体到抽象的思维过程。三.教学重、难点:1.交集与并集概念、数形结合运用;2.理解交集与并集概念、符号之间区别与联系。四.教学过程:(一)复习:子集、补集(二)新课讲解:我们观察下面五个图:说明:图1—5(1)给出了两个集合A、B;图(2)阴影部分是A与B公共部分;图(3)阴影部分是由A、B组成;图(4)集合A是集合B的真子集;图(5)集合B是集合A的真子集;指出:图(2)阴影部分叫集合A与B的交集;图(3)阴影部分叫集合A与B的并集。1.交集一般地,由所有属于A且属于B的元素所组成的集合,叫做A与B的交集。记作(读作“A交B”),即:且。仿此由学生给并集下定义:2.并集一般地,由所有属于A或属于B的元素组成的集合,叫做A与B的并集,A与B的并集,A与B的并集,记作(读作“A并B”),即或。(学生归纳以后教师给予纠正)由此图(4)说明:;图(5)说明:。3.例题解析:例1:设,,求。分析:涉及不等式有关问题,利用数形结合即运用数轴是最佳方案。解:在数轴上作出A、B对应部分如图。用心爱心专心1例2:设是等腰三角形,是直角三角形,求。分析:此题运用文氏图,其公共部分即为A∩B。解:是等腰三角形是直角三角形是等腰三角形。例3:设A={4,5,6,8},B={3,5,7,8},求A∪B。分析:运用文恩解答该题。解:∴A={4,5,6,8},B={3,5,7,8}。则A∪B={4,5,6,8}∪{3,5,7,8}={3,4,5,6,7,8}。例4:设是锐角三角形,是钝角三角,求。解:是锐角三角形是钝角三角形是斜三角形。例5:设,,求。分析:利用数轴,将A、B分别表示出来,则阴影部分即为所求。解:。五.课堂练习:课本P12,练习1—5。补充练习:已知,设,,求A∩B,A∪B。解:A∩B={(1,1)},A∪B={(1,1),(1,2),(2,1)}。六.小结:在求解问题过程中,充分利用数轴、文恩图。七.课后作业课本P13,习题1.31—6(书面表达1、3、5)。用心爱心专心2