高二数学 第六章 不等式： 6.4不等式解法举例(一)优秀教案VIP免费

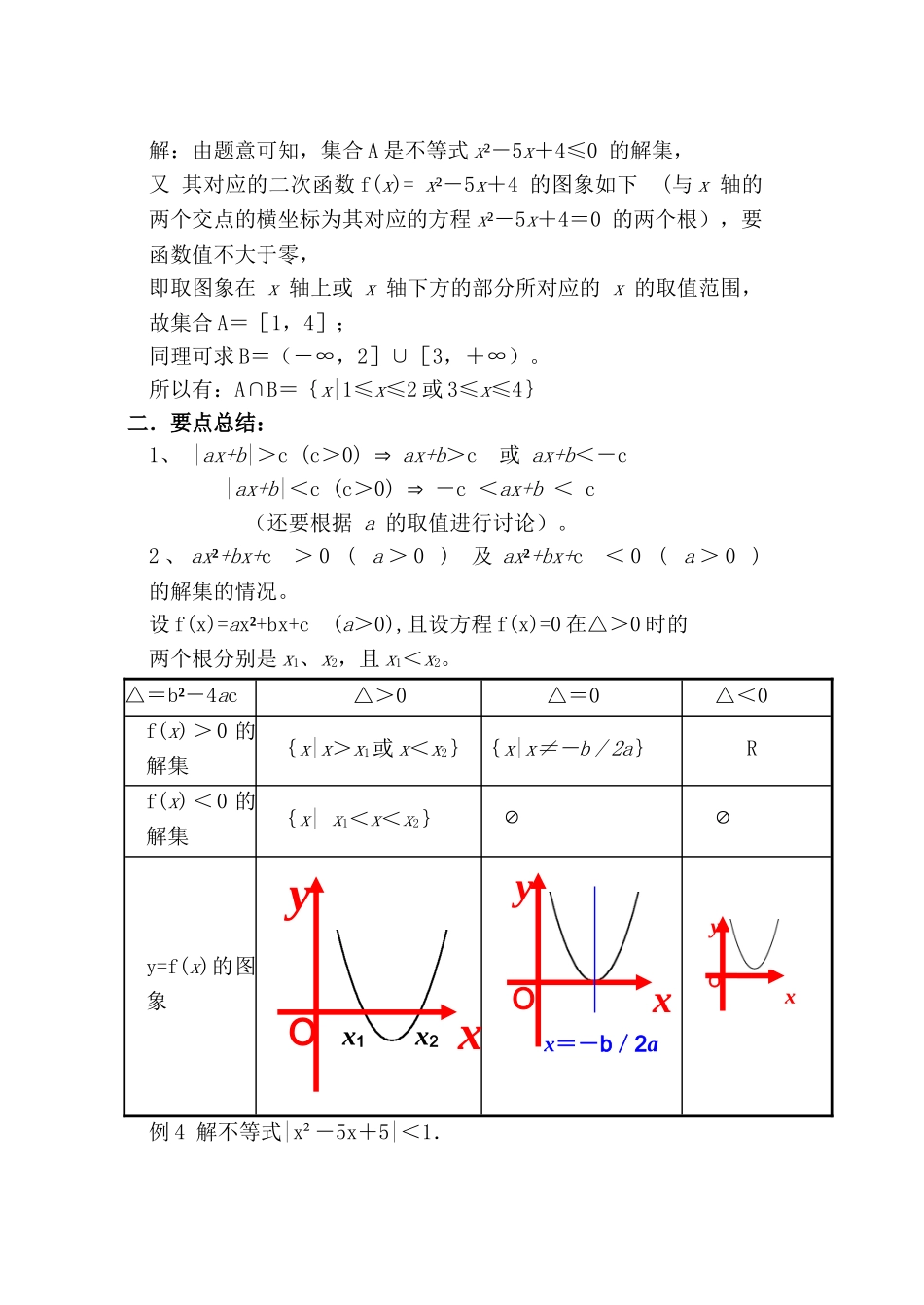
§6.4不等式解法举例(一)教材：复习一元一次不等式目的：1、理解|ax+b|＞c,|ax＋b|＜c,(c＞0)型不等式的概念，并掌握它们的解法；2、了解二次函数、一元二次不等式及一元二次方程三者之间的联系，掌握一元二次不等式的解法。3、进一步掌握|ax²+bx+c|＞k,|ax²+bx+c|＞k(k＞0)型不等式的解法。过程：一．例题示范：例1、已知集合A＝｛x｜｜x｜＜1｝，B＝｛x｜｜5－2x｜＞5｝，则A∩B＝。解：由题意可知，集合A是不等式｜x｜＜1的解集，又由｜x｜＜1Þ－1＜x＜1有：A＝（－1，1）同理，可求B＝（－∞，0）∪（5，＋∞）所以A∩B＝｛x｜－1＜x＜0｝。例2、已知集合A＝｛x｜｜x－1｜＜c,c＞0｝，B＝｛x｜｜x－3｜＞4｝，且A∩B≠Æ，求c的范围。解：由题意可知，集合A是不等式｜x－1｜＜c的解集，又由｜x－1｜＜c（c＞0）Þ1－c＜x＜1＋c有：A＝（1－c，1＋c），同理，可求B＝（－∞，－1）∪（7，＋∞）。由上图可知，要A∩B≠Æ,即要有:1－c＜－1Þc＞2所以c的范围为c＞2。例3、已知集合A＝｛x｜x²－5x＋4≤0｝，B＝｛x｜x²－5x＋6≥0｝，则A∩B＝。－11x0511－c1+cx－17解：由题意可知，集合A是不等式x²－5x＋4≤0的解集，又其对应的二次函数f(x)=x²－5x＋4的图象如下(与x轴的两个交点的横坐标为其对应的方程x²－5x＋4＝0的两个根），要函数值不大于零，即取图象在x轴上或x轴下方的部分所对应的x的取值范围，故集合A＝［1，4］；同理可求B＝（－∞，2］∪［3，＋∞）。所以有：A∩B＝｛x|1≤x≤2或3≤x≤4｝二．要点总结：1、|ax+b|＞c(c＞0)Þax+b＞c或ax+b＜－c|ax+b|＜c(c＞0)Þ－c＜ax+b＜c（还要根据a的取值进行讨论）。2、ax²+bx+c＞0(a＞0)及ax²+bx+c＜0(a＞0)的解集的情况。设f(x)=ax²+bx+c(a＞0),且设方程f(x)=0在△＞0时的两个根分别是x1、x2，且x1＜x2。△＝b²－4ac△＞0△＝0△＜0f(x)＞0的解集｛x|x＞x1或x＜x2｝｛x|x≠－b／2a｝Rf(x)＜0的解集｛x|x1＜x＜x2｝ÆÆy=f(x)的图象例4解不等式|x²－5x＋5|＜1．Oxyx1x2Oxyx＝－b／2aOxy解：原不等式可化为－1＜x²－5x＋5＜1，即解不等式①，得解集{x|1＜x＜4}．解不等式②，得解集{x|x＜2，或x＞3}．原不等式的解集是不等式①和不等式②的解集的交集，即{x|1＜x＜4}∩{x|x＜2，或x＞3}={x|1＜x＜2，或3＜x＜4}．三．反馈练习练习1、已知集合A＝｛x｜｜x－1｜＜1｝，B＝｛x｜x(x－2)＜0｝，则A∪B＝｛x｜0＜x＜2｝。练习2、若不等式ax²+bx+2＞0的解集为｛x｜－1／2＜x＜1／3｝，则a＝－12，b＝－2。练习3、(1998年高考题)设a≠b，解关于x的不等式：a²x+b²(1－x）≥［ax＋b（1－x）］²。解：∴a²x+b²(1－x)≥［ax＋b(1－x)］²Þa²x+b²－b²x≥a²x+b²(1－x)²+2abx(1－x)Þ(a²+b²－2ab)x²－(a²－b²+2b²－2ab)x≤0Þ（a－b)²(x²－x)≤0又∵a≠b，∴（a－b)²＞0故由（a－b)²(x²－x)≤0Þx²－x≤0Þx(x－1)≤0见右图有:所求不等式的解集为:{x｜0≤x≤1}四．思考题:已知集合A＝｛x｜｜x－(m＋1)²／2｜≤(m－1)²／2｝，yOx1B＝｛x｜x²－3(x＋1)x+2(3m+1)≤0，x∈R｝，若AÍB，求实数m的取值范围。分析：可解集合A＝[2m,m²+1]B＝｛x｜(x－2)[x－(3m+1)]≤0，x∈R｝集合B的解集究竟是什么？是［2，3m+1]还是［3m+1,2]?如何处理？要AÍB，又如何处理？五．课堂小结：1、熟悉|ax+b|＞c,|ax＋b|＞c,(c＞0)型不等式的概念，并掌握它们的解法；2、熟悉二次函数、一元二次不等式及一元二次方程三者之间的联系，并能运用它们之间的联系，数形结合，熟练一元二次不等式的解法。3、借助数轴进行集合间的运算。4、进一步掌握|ax²+bx+c|＞k,|ax²+bx+c|＞k(k＞0)型不等式的解法。六．作业：P18练习第1,2题P19习题6.4第1,2题