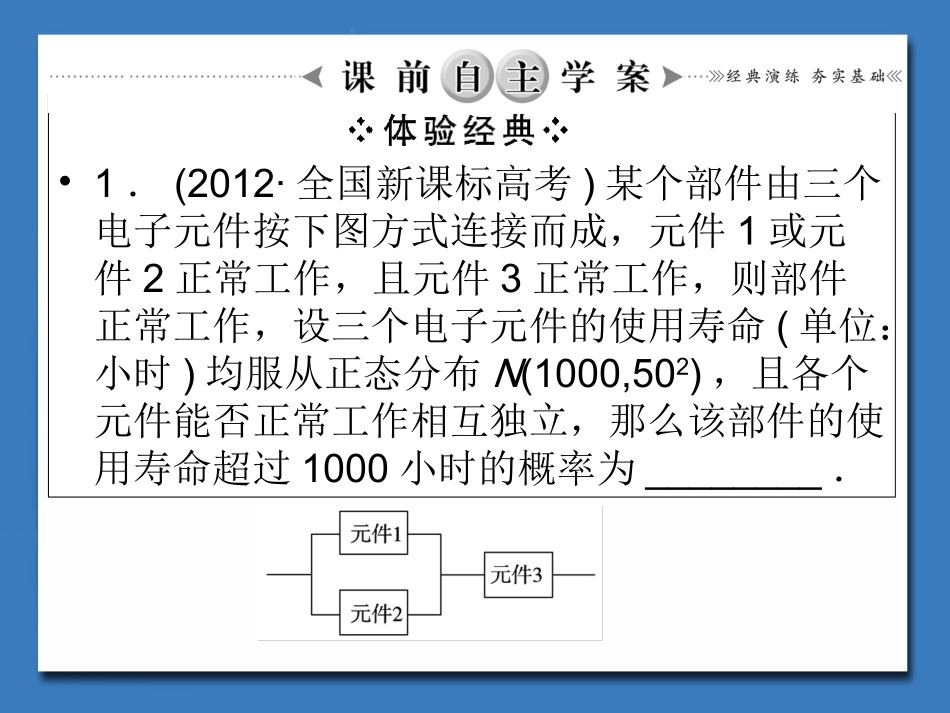
第8节离散型随机变量的均值与方差、正态分布(理)•1.(2012·全国新课标高考)某个部件由三个电子元件按下图方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作,设三个电子元件的使用寿命(单位:小时)均服从正态分布N(1000,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为________.【解析】三个电子元件的使用寿命均服从正态分布N(1000,502)得:三个电子元件的使用寿命超过1000小时的概率为p=12,超过1000小时时元件1或元件2正常工作的概率P1=1-(1-p)2=34,那么该部件的使用寿命超过1000小时的概率为p2=p1×p=38.【答案】38•2.(2011·湖北高考)已知随机变量ξ服从正态分布N(2,σ2),则P(ξ<4)=0.8,则P(0<ξ<2)=()•A.0.6B.0.4•C.0.3D.0.2【解析】 P(ξ<4)=0.8,∴P(ξ>4)=0.2,由题意知图象的对称轴为直线x=2,P(ξ<0)=P(ξ>4)=0.2,∴P(0<ξ<4)=1-P(ξ<0)-P(ξ>4)=0.6.∴P(0<ξ<2)=12P(0<ξ<4)=0.3.【答案】C•【答案】D3.(2013·潍坊模拟)设X为随机变量,X~Bn,13,若随机变量X的数学期望E(X)=2,则P(X=2)等于()A.1316B.4243C.13243D.80243【解析】 X~Bn,13,∴E(X)=n3=2.∴n=6.∴P(X=2)=C26132234=80243.•【答案】D4.(2010·山东高考)样本中共有五个个体,其值分别为a,0,1,2,3.若该样本的平均值为1,则样本方差为()A.65B.65C.2D.2【解析】由题意知a+0+1+2+3=5×1,解得,a=-1.s2=-1-12+0-12+1-12+2-12-3-125=2•5.(2010·湖北高考)某射手射击所得环数ξ的分布列如下:•已知ξ的期望E(ξ)=8.9,则y的值为__________.•【答案】0.4ξ78910Px0.10.3y【解析】依题意得x+0.1+0.3+y=1,7x+0.8+2.7+10y=8.9,即x+y=0.6,7x+10y=5.4,由此解得y=0.4.•1.均值•(1)若离散型随机变量X的分布列为Xx1x2…xi…xnPp1p2…Pi…Pn•2.方差•(1)设离散型随机变量X的分布列为Xx1x2…xi…xnPp1p2…pi…pn•1.随机变量的均值、方差与样本均值、方差的关系是怎样的?•提示:随机变量的均值、方差是一个常数,样本均值、方差是一个随机变量,随观测次数的增加或样本容量的增加,样本的值、方差趋于随机变量的均值与方差.•2.参数μ,σ在正态分布中的实际意义是什么?•提示:μ是正态分布的期望,σ是正态分布的标准差.••已知X的分布列为X-101P121316设Y=2X+3,则E(Y)的值为()A.73B.4C.-1D.1•【思路点拨】先求E(X),再根据E(Y)=E(2X+3)=2E(X)+3求出结果•【答案】A.【尝试解答】E(X)=-12+16=-13,E(Y)=E(2X+3)=2E(X)+3=-23+3=73.•【思路点拨】根据独立事件求出概率,然后按照随机变量分布列的期望公式求解.(2012·重庆高考)甲、乙两人轮流投篮,每人每次投一球.约定甲先投且先投中者获胜,一直到有人获胜或每人都已投球3次时投篮结束.设甲每次投篮投中的概率为13,乙每次投篮投中的概率为12,且各次投篮互不影响.(1)求甲获胜的概率;(2)求投篮结束时甲的投篮次数ξ的分布列与期望.【尝试解答】设Ak,Bk分别表示甲、乙在第k次投篮投中,则P(Ak)=13,P(Bk)=12,k∈(1,2,3),(1)记“甲获胜”为事件C,由互斥事件有一个发生的概率与相互独立事件同时发生的概率计算公式知,P(C)=P(A1)+P(A1B1A2)+P(A1·B1·A2·B2·A3)=P(A1)+P(A1)P(B1)P(A2)+P(A1)P(B1)P(A2)P(B2)P(A3)=13+23×12×13+232×122×13=13+19+127=1327(2)ξ的所有可能取值为:1,2,3.由独立性知:P(ξ=1)=P(A1)+P(A1B1)=13+23×12=23,P(ξ=2)=P(A1B1A2)+P(A1·B1·A2·B2)=23×12×13+232122=29,P(ξ=3)=P(A1·B1·A2·B2)=232122=19.综上知,ξ有分布列ξ123P232919从而,Eξ=1×23+2×29+3×19=139(次).•【归纳提升】(1)求离散型随机变量的期望关键是写出离散型随机变量的分布列,然后利用公式计算...