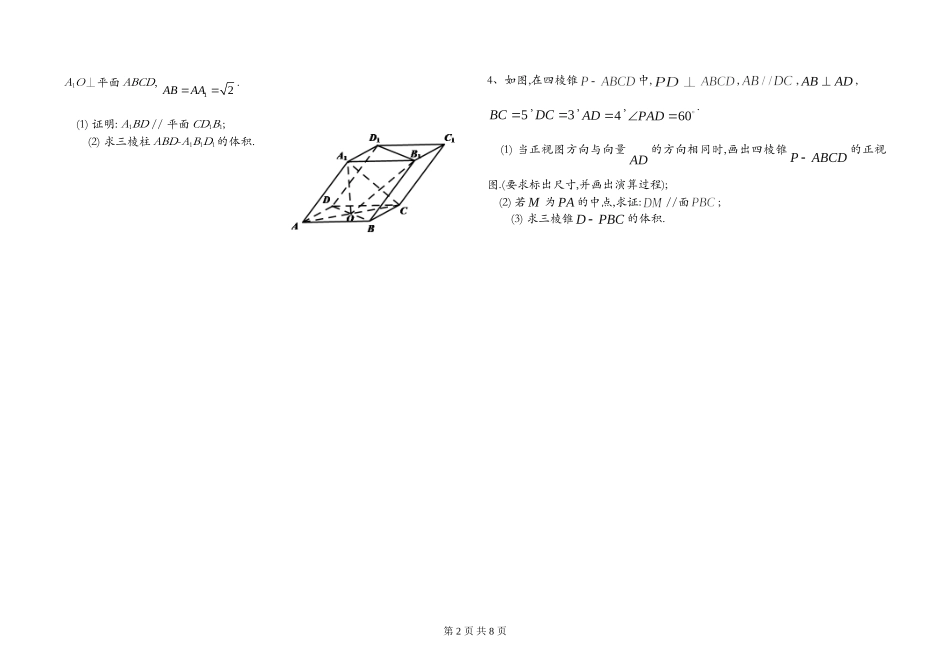
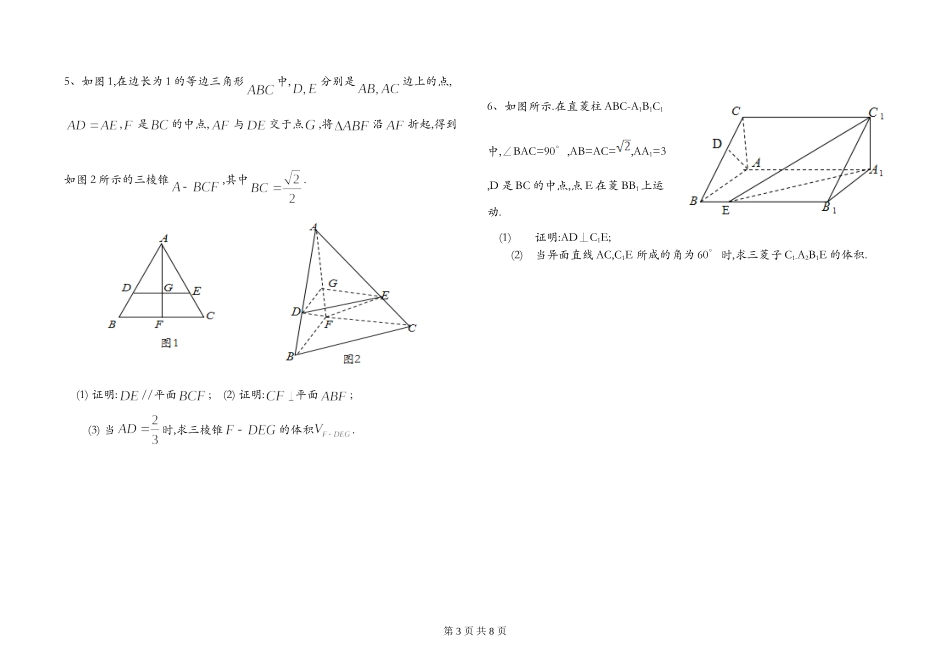
第1页共8页立体几何解答题专题训练1、如图,是圆的直径,垂直圆所在的平面,是圆上的点,(1)求证:平面;(2)设为的中点,为的重心,求证://平面.2、如图,在在四棱锥中,⊥面,==2,==,=,∠=120°,为线段上的点.(1)证明:⊥面;(2)若是的中点,求与所成的角的正切值;(3)若满足⊥面,求的值.3、如图,四棱柱ABCD-A1B1C1D1的底面ABCD是正方形,O为底面中心,第2页共8页A1O⊥平面ABCD,12ABAA.(1)证明:A1BD//平面CD1B1;(2)求三棱柱ABD-A1B1D1的体积.4、如图,在四棱锥中,,,ABAD,5BC,3DC,4AD,60PAD.(1)当正视图方向与向量AD�的方向相同时,画出四棱锥PABCD的正视图.(要求标出尺寸,并画出演算过程);(2)若M为PA的中点,求证://面;(3)求三棱锥DPBC的体积.第3页共8页5、如图1,在边长为1的等边三角形中,分别是边上的点,,是的中点,与交于点,将沿折起,得到如图2所示的三棱锥,其中.(1)证明://平面;(2)证明:平面;(3)当时,求三棱锥的体积.6、如图所示.在直菱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=,AA1=3,D是BC的中点,点E在菱BB1上运动.(1)证明:AD⊥C1E;(2)当异面直线AC,C1E所成的角为60°时,求三菱子C1-A2B1E的体积.第4页共8页7、如图,在四棱锥中,,,,平面底面,,和分别是和的中点,求证:(1)底面;(2)平面;(3)平面平面8、如图,三棱柱中,,,.(1)证明:;(2)若,,求三棱柱的体积.第5页共8页9、如图,四棱锥PABCD中,,ABACABPA,,2ABCDABCD∥,,,,,EFGMN分别为,,,,PBABBCPDPC的中点(1)求证://平面;(2)求证:平面平面10、如图,在三棱柱中,侧棱底面,,,分别是线段的中点,是线段上异于端点的点(1)在平面内,试作出过点与平面平行的直线,说明理由,并证明直线平面;(2)设(1)中的直线交于点,求三棱锥的体积.(锥体体积公式:,其中为底面面积,为高)第6页共8页11、如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点.(1)证明:BC1//平面A1CD;(2)设AA1=AC=CB=2,AB=2,求三棱锥C一A1DE的体积.12、如图,四棱锥都是边长为的等边三角形.(1)证明:(2)求点到平面的距离;第7页共8页13、如图,四棱锥PABCD的底面ABCD是边长为2的菱形,60BAD.已知2,6PBPDPA(1)证明:PCBD(2)若E为PA的中点,求三菱锥PBCE的体积.14、如图,三棱柱ABC-A1B1C1中,侧棱A1A⊥底面ABC,且各棱长均相等.D,E,F分别为棱AB,BC,A1C1的中点.(1)证明EF//平面A1CD;(2)证明平面A1CD⊥平面A1ABB1;(3)求直线BC与平面A1CD所成角的正弦值.第8页共8页15、如图,四棱锥中,⊥底面,,,.z(1)求证:⊥平面;(2)若侧棱上的点满足,求三棱锥的体积.16、如图,直四棱柱ABCD–A1B1C1D1中,AB//CD,AD⊥AB,AB=2,AD=,AA1=3,E为CD上一点,DE=1,EC=3(1)证明:BE⊥平面BB1C1C;(2)求点B1到平面EA1C1的距离