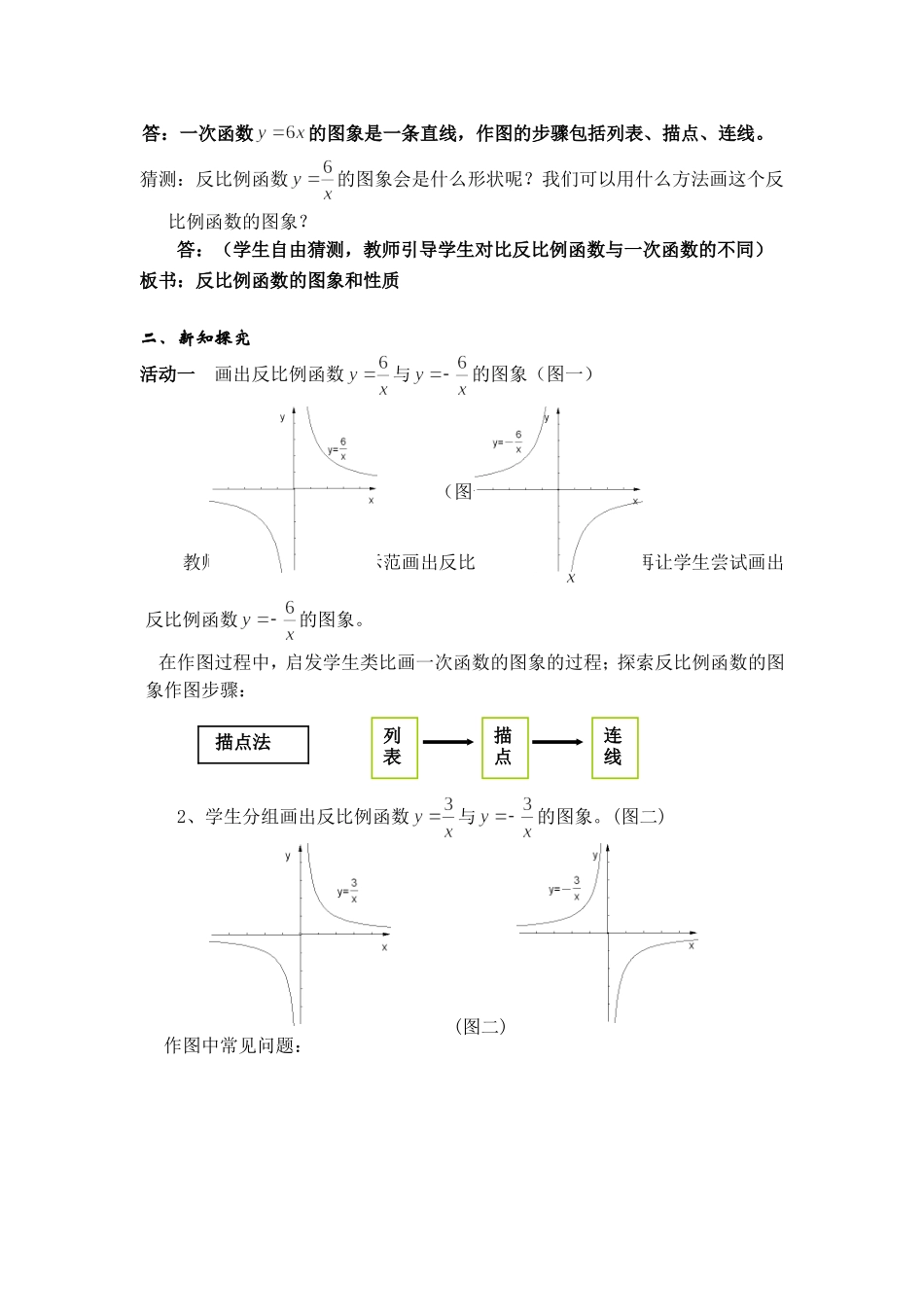
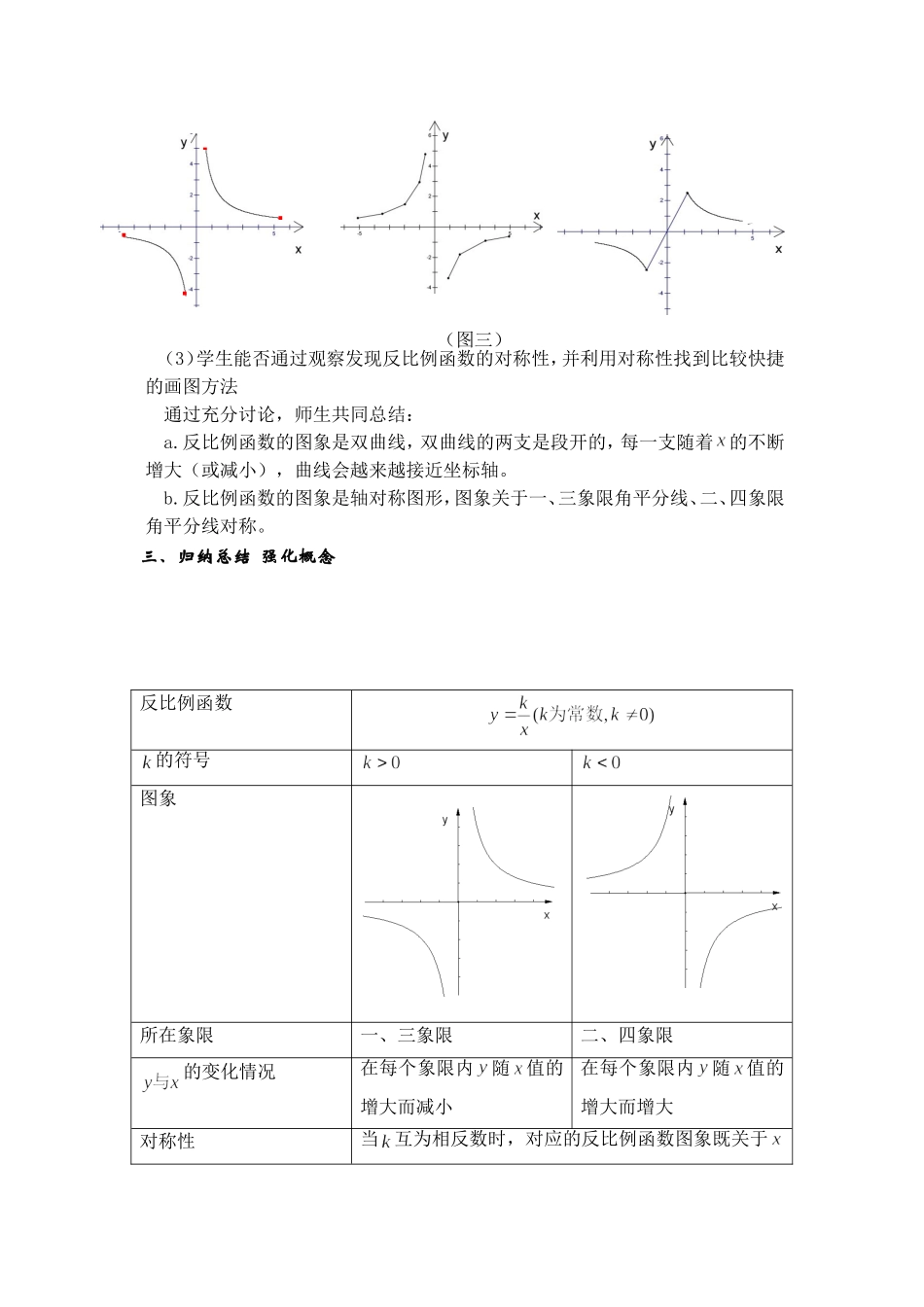
26.1.2反比例函数的图象与性质教学目标1、知识与技能1.进一步熟悉画函数图象的主要步骤,会画反比例函数的图象。2.体会函数三种表示方法的相互转换,对函数进行认识上的整合。3.逐步提高从函数图象中获取信息的能力,探索并掌握反比例函数的主要性质。2、过程与方法1.经历反比例函数主要性质的发现过程。2.体会分类讨论思想、数形结合思想的运用。3、情感态度与价值观1.积极参与探索活动,多和同伴交流看法。2.在动手画图的过程中,体会做中学的乐趣,养成勤于动手,乐于探究的好习惯。教学重点:掌握反比例函数的画图。难点:反比例函数三种表示方法的相互转换。教学用具:多媒体教学方法:类比法、数形结合法、合作、探究教学教程:一、复习巩固,情景导入问题1、教师出示投影,请同学们独立完成以下题目,1、什么是反比例函数?答:形如的函数称为反比例函数2、完成下列题目(1).任意写一个在第二象限的点的坐标:(-3,1).(2).直线y=-x+3经过第一、二、四象限.(3).已知矩形的面积为6,则它的长y与宽x之间的函数关系式为,y是x的__反比例_函数.(4).若函数y=2xm+1是反比例函数,则m=-2.(5).反比例函数,经过点(1,4_).问题2、作出一次函数的图象,图象是什么形状?作图的步骤是什么?答:一次函数的图象是一条直线,作图的步骤包括列表、描点、连线。猜测:反比例函数的图象会是什么形状呢?我们可以用什么方法画这个反比例函数的图象?答:(学生自由猜测,教师引导学生对比反比例函数与一次函数的不同)板书:反比例函数的图象和性质二、新知探究活动一画出反比例函数与的图象(图一)(图一)教师先引导学生思考,示范画出反比例函数的图象再让学生尝试画出反比例函数的图象。在作图过程中,启发学生类比画一次函数的图象的过程;探索反比例函数的图象作图步骤:2、学生分组画出反比例函数与的图象。(图二)(图二)作图中常见问题:描点法列表描点连线(图三)(3)学生能否通过观察发现反比例函数的对称性,并利用对称性找到比较快捷的画图方法通过充分讨论,师生共同总结:a.反比例函数的图象是双曲线,双曲线的两支是段开的,每一支随着的不断增大(或减小),曲线会越来越接近坐标轴。b.反比例函数的图象是轴对称图形,图象关于一、三象限角平分线、二、四象限角平分线对称。三、归纳总结强化概念反比例函数的符号图象所在象限一、三象限二、四象限的变化情况在每个象限内随值的增大而减小在每个象限内随值的增大而增大对称性当互为相反数时,对应的反比例函数图象既关于........轴对称,也关于轴对称四、当堂训练请同学们独立完成下列题目,1.反比例函数的图象大致是(D)2.如图,函数y=k/x和y=-kx+1(k≠0)在同一坐标系内的图象大致是(D)3.已知反比例函数的图象在第二、四象限,那么一次函数y=kx-k的图象经过(C)A.第一、二、三象限B.第一、二、四象限C.第一、三、四象限D.第二、三、四象限4.甲乙两地相距100km,一辆汽车从甲地开往乙地,把汽车到达乙地所用的时y(h)表示为汽车的平均速度x(km/h)的函数,则这个函数的图象大致是(C)5.若关于x,y的函数图象位于第一、三象限,则k的取值范围是k>-1.6、已知反比例函数(1)若函数的图象位于第一三象限,则k<4;(2)若在每一象限内,y随x增大而增大,则k>4.7、若点(-2,y1)、(-1,y2)、(2,y3)在反比例函数的图象上,则(B)A、y1>y2>y3B、y2>y1>y3C、y3>y1>y2D、y3>y2>y18、已知圆柱的侧面积是10πcm2,若圆柱底面半径为rcm,高为hcm,则h与r的函数图象大致是(C).五、课堂小结1.形状反比例函数的图象是由两支曲线组成的,因此称反比例函数的图象为双曲线.2.位置当k>0时,两支曲线分别位于第一、三象限内;当k<0时,两支曲线分别位于第二、四象限内.板书设计反比例函数的图象和性质画图:画图:性质步骤:步骤:图像:图像: