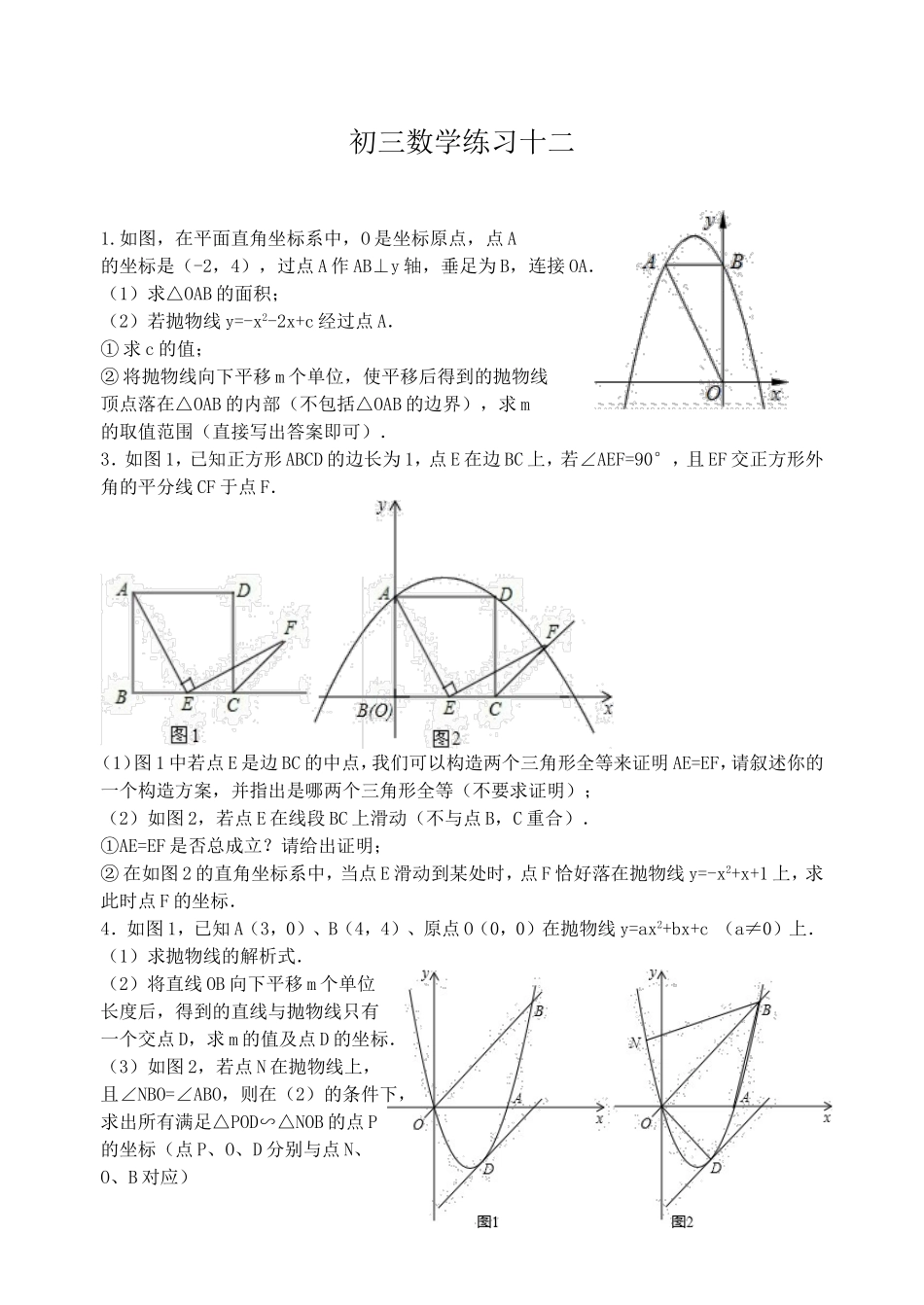
初三数学练习十二1.如图,在平面直角坐标系中,O是坐标原点,点A的坐标是(-2,4),过点A作AB⊥y轴,垂足为B,连接OA.(1)求△OAB的面积;(2)若抛物线y=-x2-2x+c经过点A.①求c的值;②将抛物线向下平移m个单位,使平移后得到的抛物线顶点落在△OAB的内部(不包括△OAB的边界),求m的取值范围(直接写出答案即可).3.如图1,已知正方形ABCD的边长为1,点E在边BC上,若∠AEF=90°,且EF交正方形外角的平分线CF于点F.(1)图1中若点E是边BC的中点,我们可以构造两个三角形全等来证明AE=EF,请叙述你的一个构造方案,并指出是哪两个三角形全等(不要求证明);(2)如图2,若点E在线段BC上滑动(不与点B,C重合).①AE=EF是否总成立?请给出证明;②在如图2的直角坐标系中,当点E滑动到某处时,点F恰好落在抛物线y=-x2+x+1上,求此时点F的坐标.4.如图1,已知A(3,0)、B(4,4)、原点O(0,0)在抛物线y=ax2+bx+c(a≠0)上.(1)求抛物线的解析式.(2)将直线OB向下平移m个单位长度后,得到的直线与抛物线只有一个交点D,求m的值及点D的坐标.(3)如图2,若点N在抛物线上,且∠NBO=∠ABO,则在(2)的条件下,求出所有满足△POD∽△NOB的点P的坐标(点P、O、D分别与点N、O、B对应)6.如图,一条抛物线经过原点和点C(8,0),A、B是该抛物线上的两点,AB∥x轴,OA=5,AB=2.点E在线段OC上,作∠MEN=∠AOC,使∠MEN的一边始终经过点A,另一边交线段BC于点F,连接AF.(1)求抛物线的解析式;2)当点F是BC的中点时,求点E的坐标;(3)当△AEF是等腰三角形时,求点E的坐标.7.关于x的方程kx2+(k+2)x+=0有两个不相等的实数根.(1)求k的取值范围;(2)当k=4时方程的两根分别为x1、x2,直接写出x1+x2,x1x2的值;(3)是否存在实数k使方程的两个实数根的倒数和等于0?若存在,求出k的值,若不存在,说明理由。8.如图,在平面直角坐标系中,Rt△ABC的斜边AB在x轴上,点C在y轴上,∠ACB=90°,OA、OB的长分别是一元二次方程x2﹣25x+144=0的两个根(OA<OB),点D是线段BC上的一个动点(不与点B、C重合),过点D作直线DE⊥OB,垂足为E.(1)求点C的坐标.(2)连接AD,当AD平分∠CAB时,求直线AD的解析式.(3)若点N在直线DE上,在坐标系平面内,是否存在这样的点M,使得C、B、N、M为顶点的四边形是正方形?若存在,请直接写出点M的坐标;若不存在,说明理由.9.已知2a-3x+1=0,3b-2x-16=0,且a≤4<b,求x的取值范围.10.如图,直线AB过点A(m,0),B(0,n)(其中m>0,n>0).反比例函数的图象与直线AB交于C,D两点,连接OC,OD.(1)已知m+n=10,△AOB的面积为S,问:当n为何值时,S取最大值?并求这个最大值;(2)若m=8,n=6,当△AOC,△COD,△DOB的面积都相等时,求p的值.11.如图,为双曲线上一点,直线平行于轴交直线于点,求(OB+AB)(OB-AB)的值12.如图,直线y=kx(k>0)与双曲线xyNMFEDBAOC交于A(x1,y1),B(x2,y2)两点,则2x1y2-7x2y1=__14.如图,面积为8的矩形的边分别在轴,轴的正半轴上,点在反比例函数的图象上,且.(1)求反比例函数的解析式(2)将矩形以点为旋转中心,顺时针旋转90°后得到矩形,反比例函数图象交于点,交于点.求的坐标.(3)△MBN的面积15.如图,已知直线与x轴、y轴分别交于点A、B,线段AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90°.(1)求△AOB的面积;(2)求点C坐标;(3)点P是x轴上的一个动点,设P(x,0)①请用x的代数式表示PB2、PC2;②是否存在这样的点P,使得|PC-PB|的值最大?如果不存在,请说明理由;如果存在,请求出点P的坐标.17.锐角△ABC中,BC=6,,两动点M,N分别在边AB,AC上滑动,且MN∥BC,以MN为边向下作正方形MPQN,设其边长为x,正方形MPQN与△ABC公共部分的面积为y(y>0).(1)求△ABC中边BC上高AD;(2)当x为何值时,PQ恰好落在边BC上(如图1);(3)当PQ在△ABC外部时(如图2),求y关于x的函数关系式(注明x的取值范围),并求出x为何值时y最大,最大值是多少?(21.如图,在矩形ABCD中,点O是边AD上的中点,点E是边BC上的一个动点,延长EO到F,使得OE=OF.FBEDCOA(1)当点E运动...