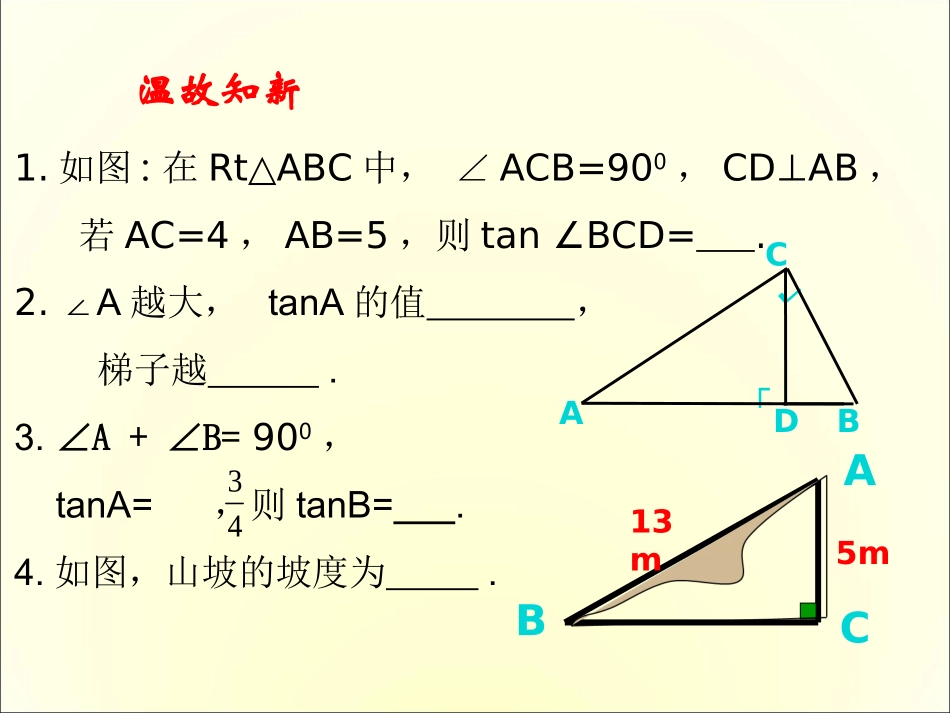
1.1.2锐角三角函数温故知新1.如图:在Rt△ABC中,∠ACB=900,CD⊥AB,若AC=4,AB=5,则tan∠BCD=.2.A∠越大,tanA的值,梯子越.3.∠A+∠B=900,tanA=,则tanB=.4.如图,山坡的坡度为.┍┌ACBDBAC5m13m34自主学习自学内容:第5页想一想前的部分自学时间:5分钟自学要求:1.掌握∠A的正弦、余弦的定义及表示方法(滚瓜烂熟)2.∠A的正弦、余弦值的大小与有关.3.计算∠A的正弦、余弦需要的条件是.合作探究小组讨论:1.sinA,cosA的大小与有关.2.sinA的范围是,cosA的范围是.3.梯子的倾斜程度与sinA,cosA的大小有关吗?4.如图:sinA=,cosB=,cosA=,sinB=,∠A与∠B的关系是:,你发现了.BCA自学检测1.第6页习题1.2第1题,随堂练习12.如图,sinA=,则cosB=,tanB=.3.∠A为锐角,化简:BCA45sin21cosAA自主学习学习内容:第5页例2和做一做学习时间:5分钟学习方式:独立学习,注意书写格式,有疑难处小组讨论.达标练习1、分别根据图(1)和图(2)求∠A的三个三角函数值.2、在Rt△ABC中,∠C=90°,(1)AC=3,AB=6,求sinA和cosB(2)BC=3,sinA=,求AC和AB.提示:求锐角三角函数时,勾股定理的运用是很重要的.┌ACB34┌ACB34(1)(2)1353.如图,在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,sinA的值()A.扩大100倍B.缩小100倍C.不变D.不能确定4.已知∠A,∠B为锐角(1)若∠A=∠B,则sinAsinB;(2)若sinA=sinB,则∠A∠B.ABC┌5.如图,∠C=90°CD⊥AB.6.在上图中,若AC=4,BC=3.则cos∠BCD=()A.B.C.D.┍┌ACBDsin.B()()()()()()35344345挑战自我1.锐角三角函数定义:∠A与∠B互余tanAtanB=1sinA=cosB的邻边的对边AAtanA=ABC∠A的对边∠A的邻边┌斜边A的对边斜边sinA=A的邻边斜边cosA=课堂小结sintancosAAA应该注意的几个问题:1.sinA,cosA,tanA,是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形).2.sinA,cosA,tanA,是一个比值.注意比的顺序,且sinA,cosA,tanA,均大于0,无单位.3.sinA,cosA,tanA,的大小只与∠A的大小有关,而与直角三角形的边长无关.铅直高度水平宽度倾斜角在实践中探索新知梯子在上升变陡过程中,下列各量的变化情况是倾斜角,铅直高度,水平宽度,梯子的长度.铅直高度水平宽度在实践中探索新知梯子在上升变陡过程中,下列各量的变化情况是倾斜角,铅直高度,水平宽度,梯子的长度.铅直高度水平宽度在实践中探索新知梯子在上升变陡过程中,下列各量的变化情况是倾斜角,铅直高度,水平宽度,梯子的长度.铅直高度水平宽度在实践中探索新知梯子在上升变陡过程中,下列各量的变化情况是倾斜角,铅直高度,水平宽度,梯子的长度.铅直高度水平宽度梯子在上升变陡过程中,下列各量的变化情况是倾斜角,铅直高度,水平宽度,梯子的长度.在实践中探索新知