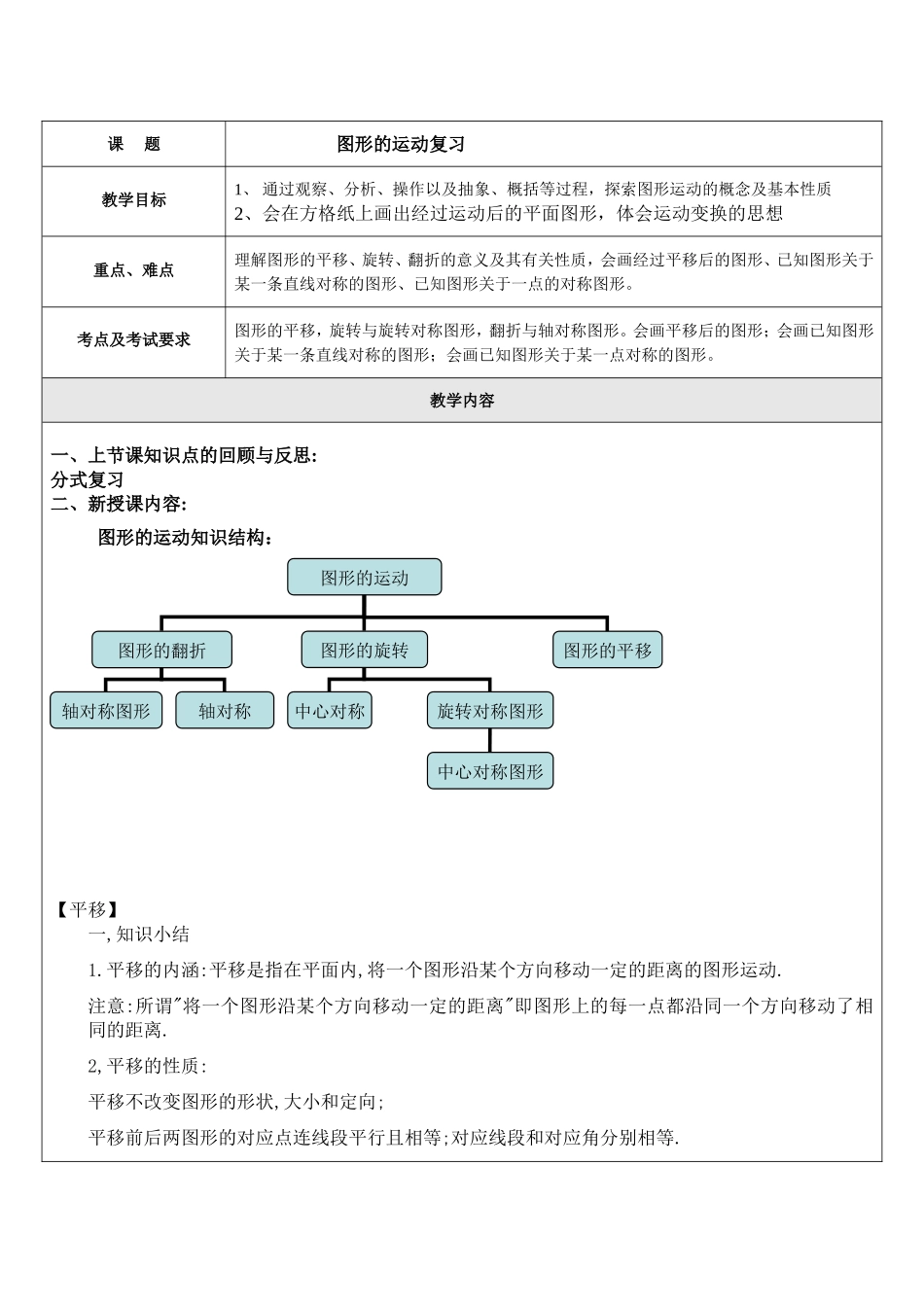
课题图形的运动复习教学目标1、通过观察、分析、操作以及抽象、概括等过程,探索图形运动的概念及基本性质2、会在方格纸上画出经过运动后的平面图形,体会运动变换的思想重点、难点理解图形的平移、旋转、翻折的意义及其有关性质,会画经过平移后的图形、已知图形关于某一条直线对称的图形、已知图形关于一点的对称图形。考点及考试要求图形的平移,旋转与旋转对称图形,翻折与轴对称图形。会画平移后的图形;会画已知图形关于某一条直线对称的图形;会画已知图形关于某一点对称的图形。教学内容一、上节课知识点的回顾与反思:分式复习二、新授课内容:图形的运动知识结构:【平移】一,知识小结1.平移的内涵:平移是指在平面内,将一个图形沿某个方向移动一定的距离的图形运动.注意:所谓"将一个图形沿某个方向移动一定的距离"即图形上的每一点都沿同一个方向移动了相同的距离.2,平移的性质:平移不改变图形的形状,大小和定向;平移前后两图形的对应点连线段平行且相等;对应线段和对应角分别相等.图形的运动图形的翻折图形的旋转图形的平移轴对称图形轴对称中心对称旋转对称图形中心对称图形3,关于平移作图:确定一个图形平移后的位置所需条件为(1)图形原来的位置;(2)平移的方向;(3)平移的距离二、【典型例题】1、在平面内,将一个图形整体沿某个___方向___,得到一个新图形。新图形改变的是图形的_____,不改变图形的____和____。2、新图形的每一点,都是由___图形中的某一点移动后得到的,这两个点就是___,连接各组对应点的线段______3、经过平移所得的图形与原来的图形的对应线段___,对应角___,对应点所连的线段____。4、图形平移时,图形上所有点移动的方向是一定的。()5、ΔABC沿射线BC方向平移到ΔA′B′C′,那么ΔA′B′C′也能沿射线BC方向平移到ΔABC。()6、如图16-54,用丁字尺画平行线,所画直线a、b互相平行的理由是。7、如图16-55,ΔABC经过运动,能够和ΔDEF重合,其中∠B=,AC=。8、如图:画出三角形ABC向右平移4个方格,再向下平移3个方格后的图形9、如图所示,请将图中的“蘑菇”向左平移6个格,再向下平移2个格.【旋转】CBA(一)定义:在平面内,将一个图形上的所有点绕一个定点按照某个方向转动一个角度,这样的运动叫做图形的旋转。这个定点叫做旋转中心,转动的角度叫做旋转角。(二)图形旋转后的性质:1、对应点到旋转中心的距离相等,对应线段的长度、对应角的大小相等。2、旋转前后图形的大小和形状没有改变。(三)旋转对称图形与中心对称图形1、旋转对称图形:把一个图形围绕着一个定点旋转一个角度α后,与初始图形重合,这种图形叫做旋转对称图形,这个定点叫做旋转对称中心,旋转的角度叫做旋转角(旋转角α满足0°α﹤﹤360°)。图形的旋转与旋转对称图形的区别和联系:①图形的旋转是指一个图形从一个位置旋转到另一个位置,是指图形在位置上的变化;旋转对称图形,是指一个图形本身旋转一定角度后位置没有变化,仍与自身重合。②图形的旋转与旋转对称图形都是绕旋转中心旋转。③识别一个图形是否为旋转对称图形,就是看是否存在一点,使图形绕着这一点旋转一定角度后能与原来的图形重合。2、中心对称图形:把一个图形绕着一个定点旋转180°后,与初始图形重合,那么这个图形叫做中心对称图形,这个点叫做对称中心.(中心对称图形是旋转对称图形的特例)中心对称图形的的性质:中心对称图形上的每一对对应点所连成的线段都经过对称中心且被对称中心平分。反之,如果两个图形的对应点连成的线段都经过某一点,并且被平分,那么这两个图形一定关于这一点成中心对称。3、把一个图形绕着一个定点旋转180°后,和另一个图形重合,那么叫做这两个图形关于这个点对称,也叫做这两个图形成中心对称,这个点叫做对称中心,这两个图形中的对应点叫做关于中心的对称点。中心对称的特征(1)中心对称是旋转对称的特例,关于中心对称的两个图形能完全重合,关于中心对称的两个图形。对称点的连线都经过对称中心并且被对称中心平分。关于中心对称的两个图形,对应线段平行(或在一条直线上)且相等;反过来,如果两...