第14讲-能量均分定理及气体速率分布律.VIP免费

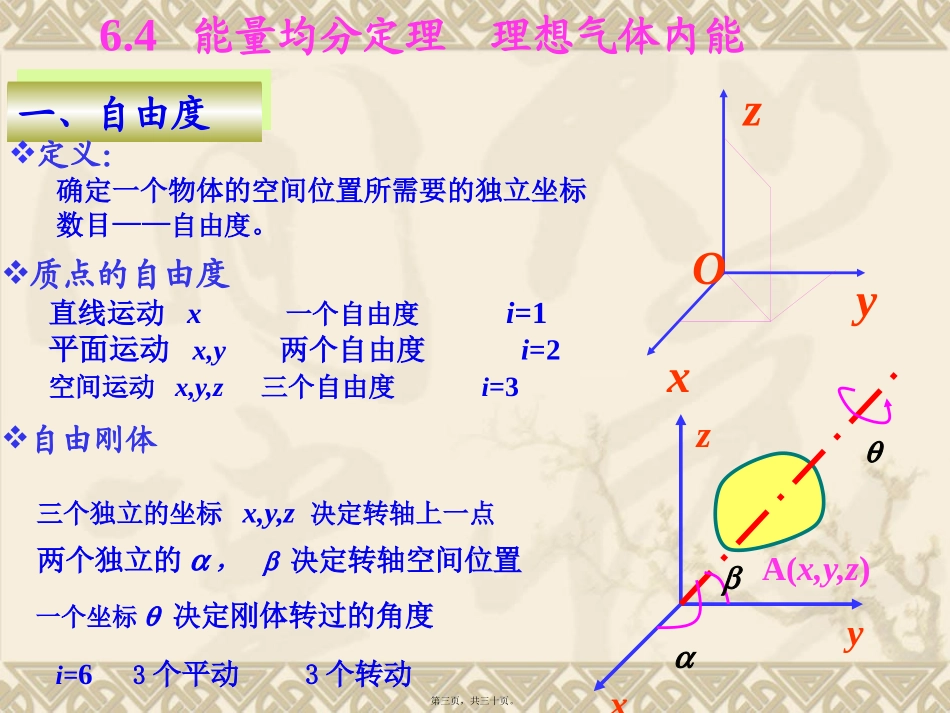
大学物理电子教案第14讲能量均分定理及气体速率分布律7.4能量均分定理理想气体内能7.5麦克斯韦气体速率分布律7.6玻尔兹曼能量分布律等温气压公式塔里木大学教学课件第一页，共三十页。复习v气体动理论的基本观点v理想气体的微观模型v理想气体压强公式knvmnp3222132)(v理想气体的温度kTvm23212第二页，共三十页。6.4能量均分定理理想气体内能一、自由度一、自由度定义：确定一个物体的空间位置所需要的独立坐标数目——自由度。质点的自由度直线运动x一个自由度i=1平面运动x,y两个自由度i=2空间运动x,y,z三个自由度i=3自由刚体i=63个平动3个转动一个坐标q决定刚体转过的角度两个独立的a，b决定转轴空间位置三个独立的坐标x,y,z决定转轴上一点xyzOA(x,y,z)xyzabq第三页，共三十页。刚性杆：x,y,z,α,βi=5刚体定轴转动：θi=1分子的自由度单原子i=3自由质点双原子i=5刚性杆多原子i=6自由刚体说明：一般来说，n≥3个原子组成的分子，共有3n个自由度，其中3个平动自由度，3个转动自由度，(3n-6)个振动自由度。当气体处于低温状态时，可把分子视为刚体。A(x,y,z)xyzabq第四页，共三十页。一个分子的平均平动能为二、能量均分定理：二、能量均分定理：kTkt23222221212121zyxkvmvmvmvm222231vvvvzyxkTvmvmvmzyx21212121222结论：分子的每一个平动自由度上具有相同的平均平动动能，都是kT/2，或者说分子的平均平动动能3kT/2是均匀地分配在分子的每一个自由度上平方项的平均值平动自由度第五页，共三十页。能量按自由度均分定理：说明：™是统计规律，只适用于大量分子组成的系统。™气体分子无规则碰撞的结果。™统计物理可给出严格证明。推广：在温度为T的平衡态下，分子的每一个转动自由度上也具有相同的平均动能，大小也为kT/2。在温度为T的平衡态下，气体分子每个自由度的平均动能都相等，都等于kT/2。这就是能量按自由度均分定理，简称能量均分定理。单原子分子i=3εk=3kT/2双原子分子i=5εk=5kT/2多原子分子i=6εk=6kT/2kTik2第六页，共三十页。热力学系统的内能热力学系统的内能是指气体分子各种形态的动能与势能的总和。即系统所包含的全部分子的能量总和称为系统的内能。三、理想气体的内能和摩尔热容三、理想气体的内能和摩尔热容1、理想气体的内能：理想气体内能公式理想气体内能是分子平动动能与转动动能之和分子的自由度为i，则一个分子能量为ikT/2，1摩尔理想气体，有个NA分子，内能RTiNkTiEA22＝m/M摩尔理想气体，内能RTiMmE2＝说明：™理想气体的内能与温度和分子的自由度有关。™内能仅是温度的函数，即E=E(T)，与P，V无关。™状态从T1→T2,不论经过什么过程，内能变化为)(21212TTRiMmEEE第七页，共三十页。2、摩尔热容定体摩尔热容RiCmV2,定压摩尔热容RiCmp22,摩尔热容比iimVmpCC2,,气体理论值实验值CV,mCP,mγCV,mCP,mγHe12.4720.781.6712.6120.951.66Ne12.5320.901.67H220.7820.091.4020.4728.831.41N220.5628.881.40O221.1629.611.40H2O24.9333.241.3327.836.21.31CH427.235.21.30CHCl363.772.01.13对于单原子分子与双原子分子，理论与实验符合得很好，而对于多原子分子，理论与实验相差较大。第八页，共三十页。四、固体热容四、固体热容设固体由N个原子组成，N个原子的三维振动，可以看成是3N个一维振动。原子作一维振动时，自由度为i=2,一项为动能，一项为势能。N个原子振动的平均能量为NkTNE331mol晶体的内能为RTkTNEA33晶体的摩尔热容111.253KmolJRdTdEdTdQCm第九页，共三十页。6.5麦克斯韦气体速率分布律引言：气体分子处于无规则的热运动之中，由于碰撞，每个分子的速度都在不断地改变，所以在某一时刻，对某个分子来说，其速度的大小和方向完全是偶然的。然而就大量分子整体而言，在一定条件下，分子的速率分布遵守一定的统计规律——气体速率分布律。气体分子按速率分布的统计规律最早是有麦克斯韦于1859年在概率论的基础上导出的，1877年玻耳兹曼由经典统计力学中导出，1920年斯特恩从实验中证实了麦克斯韦分子按速率分布的统计规律...