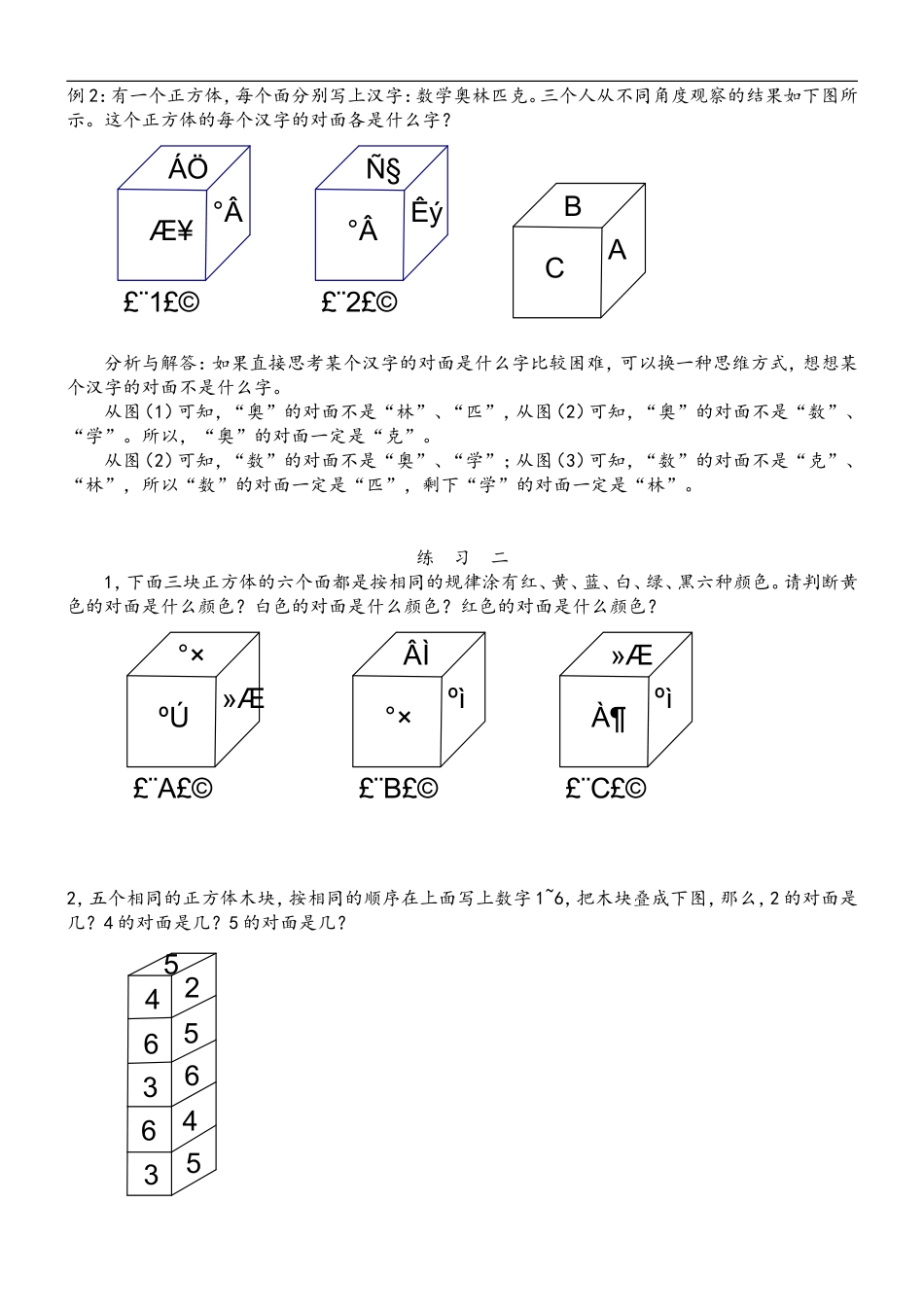
第讲:逻辑推理学生姓名年级四授课教师备课时间教学目标选准突破口,分析时综合几个条件进行判断重、难考点对可能出现的情况作出假设,然后再根据条件推理,如果得到的结论和条件不矛盾,说明假设是正确的教学内容解答推理问题常用的方法有:排除法、假设法、反证法。一般可以从以下几方面考虑:1,选准突破口,分析时综合几个条件进行判断;2,根据题中条件,在推理过程中,不断排除不可能的情况,从而得出要求的结论3,对可能出现的情况作出假设,然后再根据条件推理,如果得到的结论和条件不矛盾,说明假设是正确的;4,遇到比较复杂的推理问题,可以借助图表进行分析。例1:有三个小朋友们在谈论谁做的好事多。冬冬说:“兰兰做的比静静多。”兰兰说:“冬冬做的比静静多。”静静说:“兰兰做的比冬冬少。”这三位小朋友中,谁做的好事最多?谁做的好事最少?分析与解答:我们用“>”来表示每个小朋友之间做好事多少的关系。兰兰>静静冬冬>静静冬冬>兰兰所以,冬冬>兰兰>静静,冬冬做的好事最多,静静做的最少。练习一1,卢刚、丁飞和陈瑜一位是工程师,一位是医生,一位是飞行员。现在只知道:卢刚和医生不同岁;医生比丁飞年龄小,陈瑜比飞行员年龄大。问:谁是工程师、谁是医生、谁是飞行员?2,江波、刘晓、吴萌三个老师,其中一位教语文,一位教数学,一位教英语。已知:江波和语文老师是邻居;吴萌和语文老师不是邻居;吴萌和数学老师是同学。请问:三个老师分别教什么科目?基础狂记例题狂学例2:有一个正方体,每个面分别写上汉字:数学奥林匹克。三个人从不同角度观察的结果如下图所示。这个正方体的每个汉字的对面各是什么字?£¨1£©°ÂÆ¥ÁÖ£¨2£©Êý°ÂѧACB分析与解答:如果直接思考某个汉字的对面是什么字比较困难,可以换一种思维方式,想想某个汉字的对面不是什么字。从图(1)可知,“奥”的对面不是“林”、“匹”,从图(2)可知,“奥”的对面不是“数”、“学”。所以,“奥”的对面一定是“克”。从图(2)可知,“数”的对面不是“奥”、“学”;从图(3)可知,“数”的对面不是“克”、“林”,所以“数”的对面一定是“匹”,剩下“学”的对面一定是“林”。练习二1,下面三块正方体的六个面都是按相同的规律涂有红、黄、蓝、白、绿、黑六种颜色。请判断黄色的对面是什么颜色?白色的对面是什么颜色?红色的对面是什么颜色?£¨A£©»ÆºÚ°×£¨B£©ºì°×ÂÌ£¨C£©ºìÀ¶»Æ2,五个相同的正方体木块,按相同的顺序在上面写上数字1~6,把木块叠成下图,那么,2的对面是几?4的对面是几?5的对面是几?54652363645例3:甲、乙、丙三个孩子踢球打碎了玻璃,甲说:“是丙打碎的。”乙说:“我没有打碎破璃。”丙说:“是乙打碎的。”他们当中有一个人说了谎话,到底是谁打碎了玻璃?分析与解答:由题意推出结论,必须符合他们中只有一个人说了谎,推理时可先假设,看结论和条件是否矛盾。如果是甲打碎的,那么甲说谎话,乙说的是真话,丙说的是谎话。这样两人说的是谎话,与他们中只有一人说谎相矛盾,所以不是甲打碎的。如果是乙打碎的,那么甲说的是谎话,乙说的是谎话,丙说的是真话,与他们中只有一人说谎相矛盾,所以不是乙打碎的。如果是丙打碎的,那么甲说的是真话,乙说的是真话,而丙说的是谎话。这样有两个说的是真话,符合条件中只有一个人说的是谎话,所以玻璃是丙打碎的。练习三1,已知甲、乙、丙三人中,只有一人会开汽车。甲说:“我会开汽车。”乙说:“我不会开。”丙说:“甲不会开汽车。”如果三人中只有一人讲的是真话,那么谁会开汽车?2,A、B、C、D四个孩子踢球打碎了玻璃。A说:“是C或D打碎的。”B说:“是D打碎的。”C说:“我没有打碎玻璃。”D说:“不是我打碎的。”他们中只有一个人说了谎,到底是谁打碎了玻璃?例4:甲、乙、丙、丁四个人同时参加数学竞赛。最后:甲说:“丙是第一名,我是第三名。”乙说:“我是第一名,丁是第四名。”丙说:“丁是第一名,我是第三名。”丁没有说话。成绩揭晓时,大家发现甲、乙、丙三个人各说对了一半。你能说出他们的名次吗?分析与解答:推理...