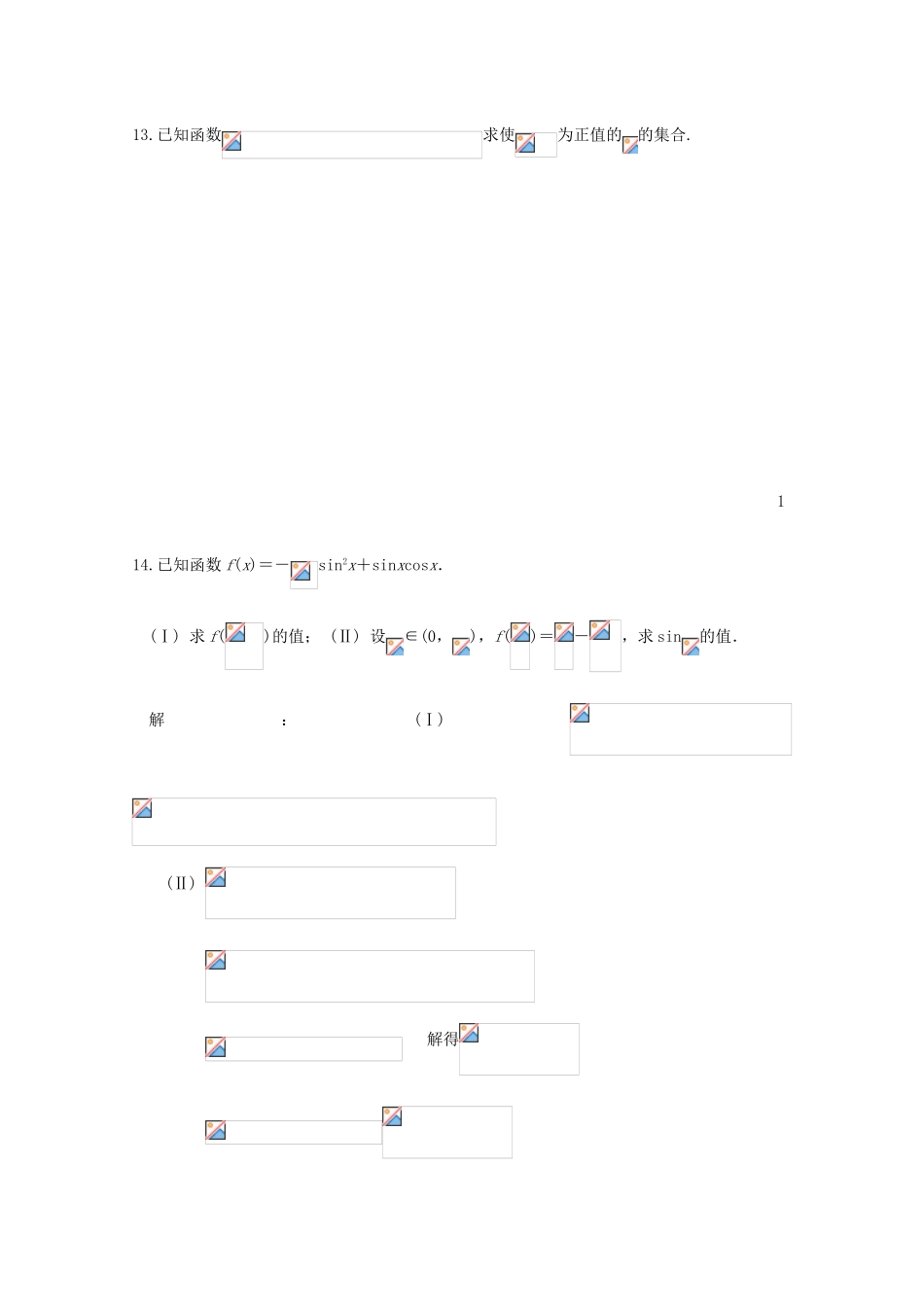
三角函数23解答题9.解10.已知=2,求(I)的值;(II)的值.解:(I)∵tan=2,∴;所以=;(II)由(I),tanα=-,所以==.11.设函数图像的一条对称轴是直线。(Ⅰ)求;(Ⅱ)求函数的单调增区间;(Ⅲ)画出函数在区间上的图像。本小题主要考查三角函数性质及图像的基本知识,考查推理和运算能力,满分12分.解:(Ⅰ)的图像的对称轴,(Ⅱ)由(Ⅰ)知由题意得所以函数(Ⅲ)由x0y-1010故函数13.已知函数求使为正值的的集合.114.已知函数f(x)=-sin2x+sinxcosx.(Ⅰ)求f()的值;(Ⅱ)设∈(0,),f()=-,求sin的值.解:(Ⅰ)(Ⅱ)解得15.已知函数f(x)=2sinxcosx+cos2x.(Ⅰ)求f()的值;(Ⅱ)设∈(0,),f()=,求sin的值.16.已知向量.求函数f(x)的最大值,最小正周期,并写出f(x)在[0,π]上的单调区间.解:=.所以,最小正周期为上单调增加,上单调减少.17.已知在△ABC中,sinA(sinB+cosB)-sinC=0,sinB+cos2C=0,求角A、B、C的大小.解:由由、,所以即由得所以即因为,所以由从而,知B+2C=不合要求.再由,得所以18.若函数的最大值为2,试确定常数a的值.19.若函数的最大值为,试确定常数a的值.20.已知.(I)求sinx-cosx的值;(Ⅱ)求的值.本小题主要考查三角函数的基本公式、三角恒等变换、三角函数在各象限符号等基本知识,以及推理和运算能力.满分12分.解法一:(Ⅰ)由即又故(Ⅱ)21.已知向量,求的值.解法一:由已知,得又所以22.已知.解:由题设条件,应用两角差的正弦公式得即①由题设条件,应用二倍角余弦公式得故②由①式和②式得.因此,,由两角和的正切公式