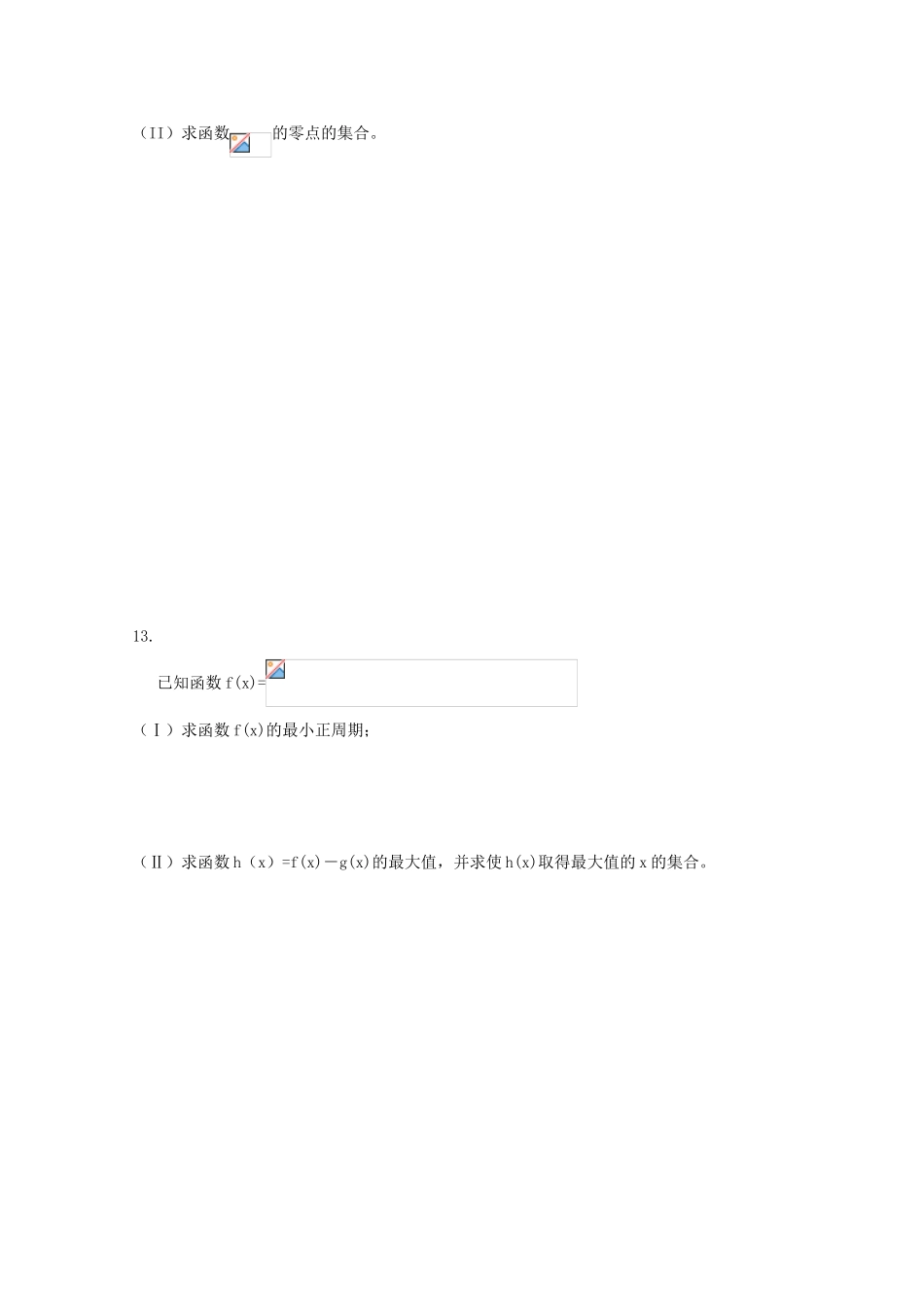
三角函数1611.已知函数在时取得最大值4.(1)求的最小正周期;(2)求的解析式;(3)若(α+)=,求sinα.,,,,.12.已知函数.(Ⅰ)求函数的最大值;(II)求函数的零点的集合。13.已知函数f(x)=(Ⅰ)求函数f(x)的最小正周期;(Ⅱ)求函数h(x)=f(x)-g(x)的最大值,并求使h(x)取得最大值的x的集合。14.。,轮船位于港口O北偏西且与该港口相距20海里的A处,并以30海里/小时的航行速度沿正东方向匀速行驶。假设该小船沿直线方向以海里/小时的航行速度匀速行驶,经过t小时与轮船相遇。(1)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?(2)假设小艇的最高航行速度只能达到30海里/小时,试设计航行方案(即确定航行方向与航行速度的大小),使得小艇能以最短时间与轮船相遇,并说明理由。此时,在中,,故可设计航行方案如下:航行方向为北偏东,航行速度为30海里/小时,小艇能以最短时间与轮船相遇。15.某兴趣小组测量电视塔AE的高度H(单位:m),如示意图,垂直放置的标杆BC的高度h=4m,仰角∠ABE=,∠ADE=。(1)该小组已经测得一组、的值,tan=1.24,tan=1.20,请据此算出H的值;(2)该小组分析若干测得的数据后,认为适当调整标杆到电视塔的距离d(单位:m),使与之差较大,可以提高测量精确度。若电视塔的实际高度为125m,试问d为多少时,-最大?解析]本题主要考查解三角形的知识、两角差的正切及不等式的应用。(1),同理:,。AD—AB=DB,故得,解得:。因此,算出的电视塔的高度H是124m。(2)由题设知,得,,(当且仅当时,取等号)故当时,最大。因为,则,所以当时,-最大。故所求的是m。16.已知△ABC的三边长都是有理数。(1)求证cosA是有理数;(2)求证:对任意正整数n,cosnA是有理数。解析]本题主要考查余弦定理、数学归纳法等基础知识,考查推理论证的能力与分析问题、解决问题的能力。满分10分。②假设当时,结论成立,即coskA、均是有理数。当时,,,,解得:∵cosA,,均是有理数,∴是有理数,∴是有理数。即当时,结论成立。综上所述,对于任意正整数n,cosnA是有理数。