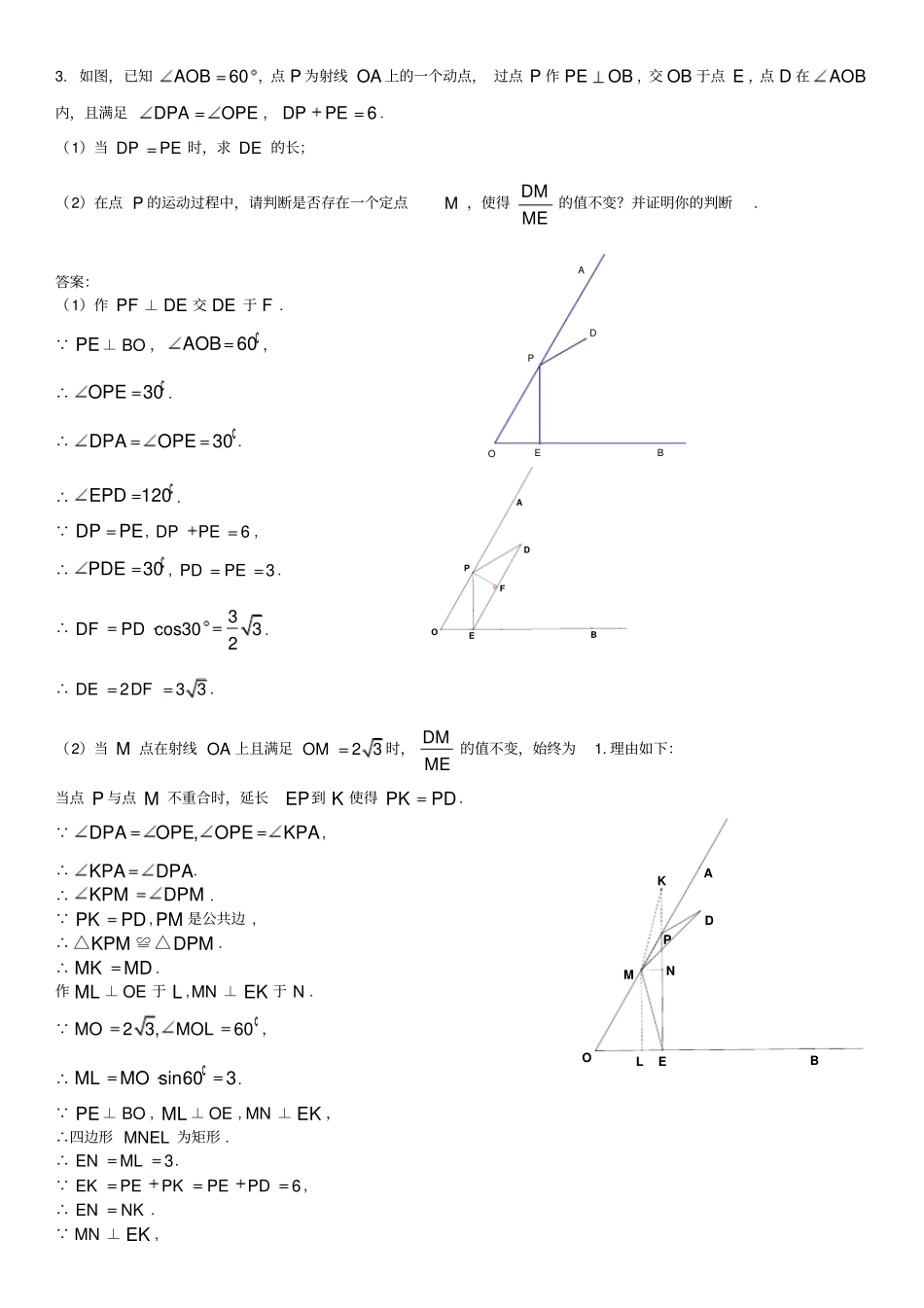
几何综合题1.已知△ABC中,AD是的平分线,且AD=AB,过点C作AD的垂线,交AD的延长线于点H.(1)如图1,若①直接写出B和ACB的度数;②若AB=2,求AC和AH的长;(2)如图2,用等式表示线段AH与AB+AC之间的数量关系,并证明.答案:(1)①75B,45ACB;②作DE⊥AC交AC于点E.Rt△ADE中,由30DAC,AD=2可得DE=1,AE3.Rt△CDE中,由45ACD,DE=1,可得EC=1.∴AC31.Rt△ACH中,由30DAC,可得AH332;(2)线段AH与AB+AC之间的数量关系:2AH=AB+AC证明:延长AB和CH交于点F,取BF中点G,连接GH.易证△ACH≌△AFH.∴ACAF,HCHF.∴GHBC∥. ABAD,∴ABDADB.∴AGHAHG.∴AGAH.∴2222ABACABAFABBFABBGAGAH.2.正方形ABCD的边长为2,将射线AB绕点A顺时针旋转,所得射线与线段BD交于点M,作CEAM于点E,点N与点M关于直线CE对称,连接CN.(1)如图1,当045时,①依题意补全图1.②用等式表示NCE与BAM之间的数量关系:__________.BAC60BAC(2)当4590时,探究NCE与BAM之间的数量关系并加以证明.(3)当090时,若边AD的中点为F,直接写出线段EF长的最大值.答案:(1)①补全的图形如图7所示.②∠NCE=2∠BAM.(2)当45°<α<90°时,=1802NCEBAM.证明:如图8,连接CM,设射线AM与CD的交点为H. 四边形ABCD为正方形,∴∠BAD=∠ADC=∠BCD=90°,直线BD为正方形ABCD的对称轴,点A与点C关于直线BD对称. 射线AM与线段BD交于点M,∴∠BAM=∠BCM=α.∴∠1=∠2=90. CE⊥AM,∴∠CEH=90°,∠3+∠5=90°.又 ∠1+∠4=90°,∠4=∠5,∴∠1=∠3.∴∠3=∠2=90. 点N与点M关于直线CE对称,∴∠NCE=∠MCE=∠2+∠3=1802BAM.(3)21CDBA图1备用图CDBAM3.如图,已知60AOB,点P为射线OA上的一个动点,过点P作PEOB,交OB于点E,点D在AOB内,且满足DPAOPE,6DPPE.(1)当DPPE时,求DE的长;(2)在点P的运动过程中,请判断是否存在一个定点M,使得DMME的值不变?并证明你的判断.答案:(1)作PF⊥DE交DE于F. PE⊥BO,60AOB,∴30OPE.∴30DPAOPE.∴120EPD. DPPE,6DPPE,∴30PDE,3PDPE.∴3cos3032DFPD.∴233DEDF.(2)当M点在射线OA上且满足23OM时,DMME的值不变,始终为1.理由如下:当点P与点M不重合时,延长EP到K使得PKPD. ,DPAOPEOPEKPA,∴KPADPA.∴KPMDPM. PKPD,PM是公共边,∴KPM△≌DPM△.∴MKMD.作ML⊥OE于L,MN⊥EK于N. 23,60MOMOL,∴sin603MLMO. PE⊥BO,ML⊥OE,MN⊥EK,∴四边形MNEL为矩形.∴3ENML. 6EKPEPKPEPD,∴ENNK. MN⊥EK,BAOEDPFDEOBAPLNMDKEOBAP∴MKME.∴MEMKMD,即1DMME.当点P与点M重合时,由上过程可知结论成立.4.如图,在菱形ABCD中,∠DAB=60°,点E为AB边上一动点(与点A,B不重合),连接CE,将∠ACE的两边所在射线CE,CA以点C为中心,顺时针旋转120°,分别交射线AD于点F,G.(1)依题意补全图形;(2)若∠ACE=α,求∠AFC的大小(用含α的式子表示);(3)用等式表示线段AE、AF与CG之间的数量关系,并证明.答案:(1)补全的图形如图所示.(2)解:由题意可知,∠ECF=∠ACG=120°.∴∠FCG=∠ACE=α. 四边形ABCD是菱形,∠DAB=60°,∴∠DAC=∠BAC=30°.∴∠AGC=30°.∴∠AFC=α+30°.(3)用等式表示线段AE、AF与CG之间的数量关系为CGAFAE3.证明:作CH⊥AG于点H.由(2)可知∠BAC=∠DAC=∠AGC=30°.∴CA=CG.∴HG=21AG. ∠ACE=∠GCF,∠CAE=∠CGF,∴△ACE≌△GCF.∴AE=FG.在Rt△HCG中,.23cosCGCGHCGHG∴AG=3CG.即AF+AE=3CG.5.如图,Rt△ABC中,∠ACB=90°,CA=CB,过点C在△ABC外作射线CE,且∠BCE=,点B关于CE的对称点为点D,连接AD,BD,CD,其中AD,BD分别交射线CE于点M,N.(1)依题意补全图形;(2)当=30°时,直接写出∠CMA的度数;(3)当0°<<45°时,用等式表示线段AM,CN之间的数量关系,并证明.答案:(1)如图;(2)45°;(3)结论:AM=2CN.ABCE证明:作AG⊥EC的延长线于点G. 点B与点D关于CE对称,∴CE是BD的垂直平分线.∴CB=CD.∴∠1=∠2=. CA=CB,∴CA=CD.∴∠3=∠CAD. ∠4=90°,∴∠3=(180°∠ACD)=(180°90°)=45°.∴∠5=∠2+∠3=+45°-=45°. ∠4=90°,CE是BD的垂直平分线,∴∠1+∠7=90°,∠1+∠6=90°.∴∠6=∠7. AG⊥EC,...