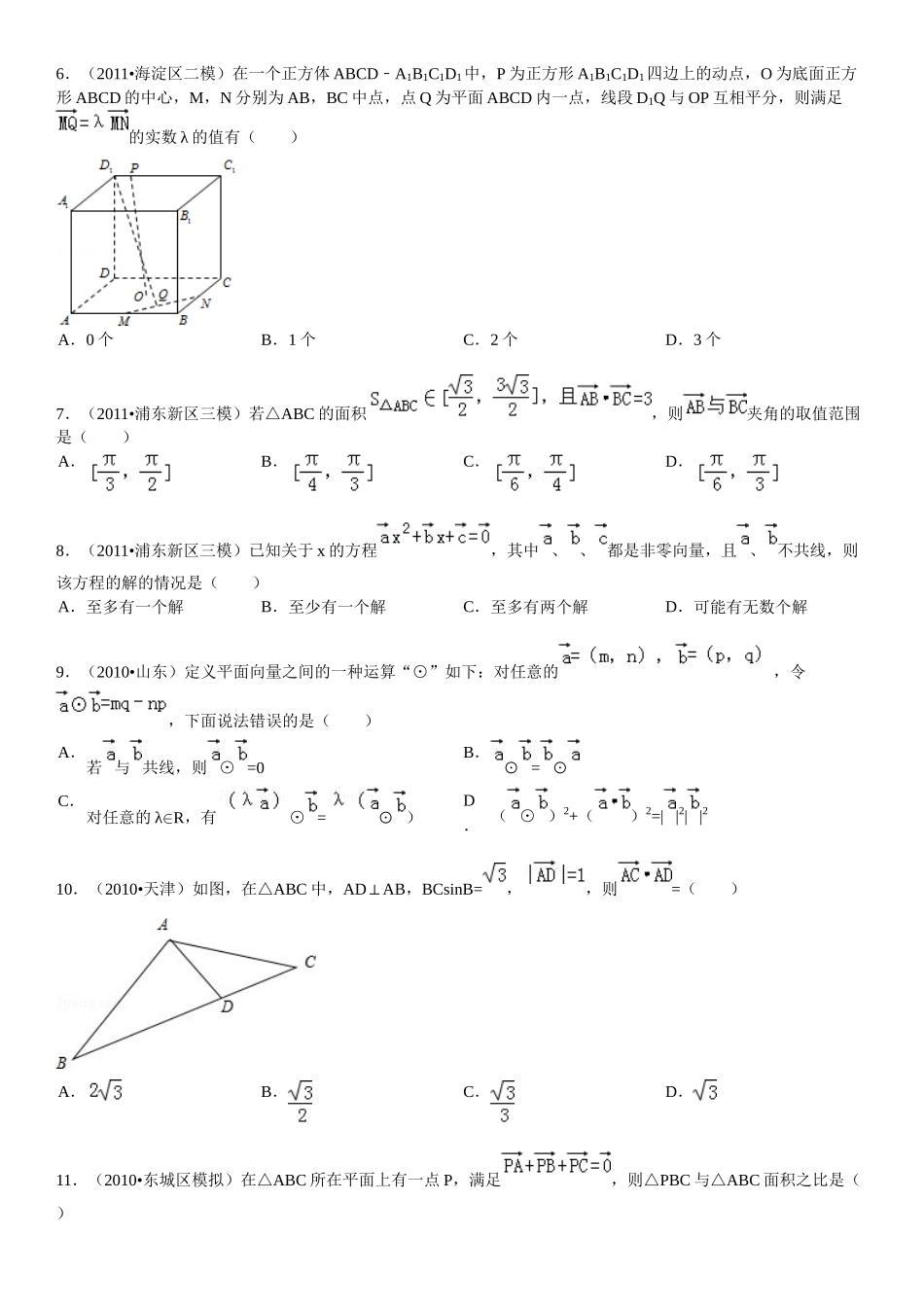
2015年高中数学向量的综合应用填选拔高题组一.选择题(共15小题)1.(2011•上海)设A1,A2,A3,A4,A5是平面上给定的5个不同点,则使=成立的点M的个数为()A.0B.1C.5D.102.(2011•山东)设A1,A2,A3,A4是平面直角坐标系中两两不同的四点,若(λ∈R),(μ∈R),且,则称A3,A4调和分割A1,A2,已知点C(c,0),D(d,O)(c,d∈R)调和分割点A(0,0),B(1,0),则下面说法正确的是()A.C可能是线段AB的中点B.D可能是线段AB的中点C.C,D可能同时在线段AB上D.C,D不可能同时在线段AB的延长线上3.(2011•浦东新区模拟)若在直线l上存在不同的三个点A,B,C,使得关于实数x的方程x2+x+=有解(点O不在l上),则此方程的解集为()A.{1}﹣B.{0}C.D.{1﹣,0}4.(2011•咸阳三模)已知双曲线的左顶点为A1,右焦点为F2,P为双曲线右支上一点,则的最小值为()A.2﹣B.C.1D.05.(2011•淄博二模)函数(1<x<4)的图象如图所示,A为图象与x轴的交点,过点A的直线l与函数的图象交于B,C两点,则(+)•=()A.8﹣B.4﹣C.4D.86.(2011•海淀区二模)在一个正方体ABCDA﹣1B1C1D1中,P为正方形A1B1C1D1四边上的动点,O为底面正方形ABCD的中心,M,N分别为AB,BC中点,点Q为平面ABCD内一点,线段D1Q与OP互相平分,则满足的实数λ的值有()A.0个B.1个C.2个D.3个7.(2011•浦东新区三模)若△ABC的面积,则夹角的取值范围是()A.B.C.D.8.(2011•浦东新区三模)已知关于x的方程,其中、、都是非零向量,且、不共线,则该方程的解的情况是()A.至多有一个解B.至少有一个解C.至多有两个解D.可能有无数个解9.(2010•山东)定义平面向量之间的一种运算“⊙”如下:对任意的,令,下面说法错误的是()A.若与共线,则⊙=0B.⊙=⊙C.对任意的λ∈R,有⊙=⊙)D.(⊙)2+()2=||2||210.(2010•天津)如图,在△ABC中,ADAB⊥,BCsinB=,,则=()A.B.C.D.11.(2010•东城区模拟)在△ABC所在平面上有一点P,满足,则△PBC与△ABC面积之比是()A.B.C.D.12.(2010•青浦区一模)设、、为同平面内具有相同起点的任意三个非零向量,且满足与不共线,,,则的值一定等于()A.以、为两边的三角形面积B.以、为邻边的平行四边形的面积C.以、为两边的三角形面积D.以、为邻边的平行四边形的面积13.(2010•黄冈模拟)平面向量的集合A到A的映射f由f()=确定,其中为常向量.若映射f满足对恒成立,则的坐标不可能是()A.(0,0)B.(﹣,)C.(﹣,)D.(﹣,)14.(2010•浙江模拟)设G是△ABC的重心,且,则B的大小为()A.45°B.60°C.30°D.15°15.(2010•湖北模拟)△ABC内接于以O为圆心,半径为1的圆,且,则△ABC的面积为()A.1B.C.D.二.填空题(共15小题)16.(2013•重庆)OA为边,OB为对角线的矩形中,,,则实数k=_________.17.(2013•山东)在平面直角坐标系xOy中,已知,,若∠ABO=90°,则实数t的值为_________.18.(2013•浙江)设、为单位向量,非零向量=x+y,x、y∈R.若、的夹角为30°,则的最大值等于_________.19.(2013•北京)已知点A(1,﹣1),B(3,0),C(2,1).若平面区域D由所有满足(1≤λ≤2,0≤μ≤1)的点P组成,则D的面积为_________.20.(2013•牡丹江一模)如图矩形ORTM内放置5个大小相同的边长为1的正方形,其中A,B,C,D都在矩形的边上,若向量,则x2+y2=_________.21.(2013•佛山一模)(几何证明选讲)如图,M是平行四边形ABCD的边AB的中点,直线l过点M分别交AD,AC于点E,F.若AD=3AE,则AF:FC=_________.22.(2013•嘉定区一模)给定2个长度为1且互相垂直的平面向量和,点C在以O为圆心的圆弧上运动,若=,其中x,y∈R,则(x1﹣)2+y2的最大值为_________.23.(2012•安徽)若平面向量满足|2|≤3,则的最小值是_________.24.(2012•黑龙江)已知向量夹角为45°,且,则=_________.25.(2012•湖南)如图,在平行四边形ABCD中,APBD⊥,垂足为P,且AP=3,则=_________.26.(2012•北京)己知正方形ABCD的边长为1,点E是AB边上的动...