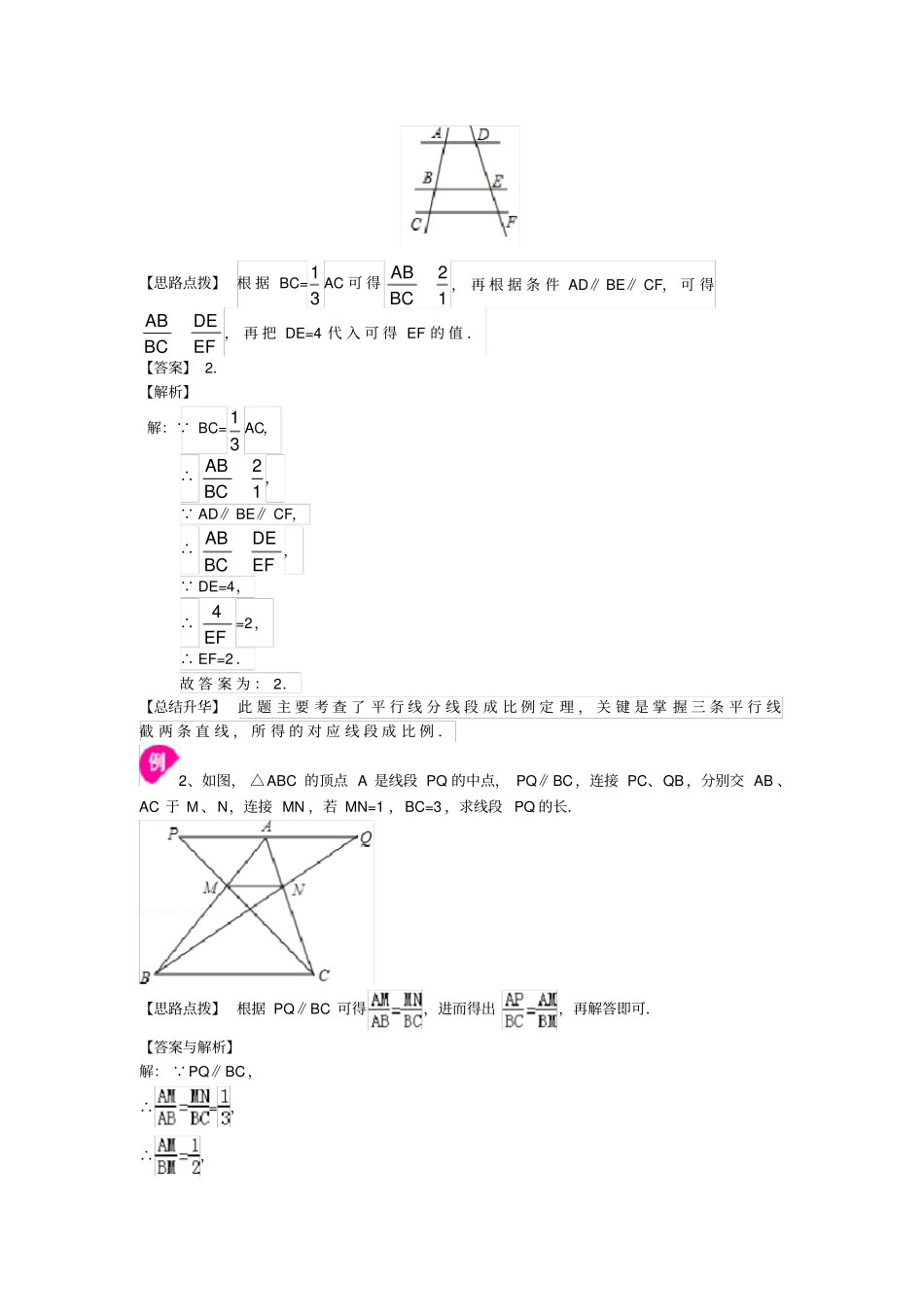
平行线分线段成比例及相似多边形【学习目标】1.平行线分线段成比例及其推论.2.平行线分线段成比例及其推论的应用.3.相似多边形的有关概念.【要点梳理】要点一、平行线分线段成比例及其推论平行线分线段成比例,一般地,有如下基本事实:两条直线被一组平行线所截,所得的对应线段成比例.推论:平行于三角形一边的直线与其他两边相交,截得的对应线段成比例.要点诠释:(1).对应线段成比例可用下面的语言形象表示:右全左全右上左上全上全上下上下上,,等等.(2)有推论可以得出以下结论:要点二、行线分线段成比例及其推论的应用行线分线段成比例及其推论的应用主要是来求线段的长度.要点三、相似多边形的有关概念相似多边形:各角分别相等、各边成比例的两个多边形叫做相似多边形.它的符号是“∽”,读作“相似于”.相似比:相似多边形的对应边的比叫做相似比.要点诠释:(1)相似图形就是指形状相同,但大小不一定相同的图形;(2)“全等”是“相似”的一种特殊情况,即当“形状相同”且“大小相同”时,两个图形是全等.(3)相似多边形的定义既是判定方法,又是它的性质.【典型例题】类型一、平行线分线段成比例及其推论1、如图,直线AD∥BE∥CF,BC=13AC,DE=4,那么EF的值是__________.【思路点拨】根据BC=13AC可得21ABBC,再根据条件AD∥BE∥CF,可得ABDEBCEF,再把DE=4代入可得EF的值.【答案】2.【解析】解: BC=13AC,∴21ABBC, AD∥BE∥CF,∴ABDEBCEF, DE=4,∴4EF=2,∴EF=2.故答案为:2.【总结升华】此题主要考查了平行线分线段成比例定理,关键是掌握三条平行线截两条直线,所得的对应线段成比例.2、如图,△ABC的顶点A是线段PQ的中点,PQ∥BC,连接PC、QB,分别交AB、AC于M、N,连接MN,若MN=1,BC=3,求线段PQ的长.【思路点拨】根据PQ∥BC可得,进而得出,再解答即可.【答案与解析】解: PQ∥BC,∴=,∴,∴, AP=AQ,∴PQ=3.【总结升华】此题考查了平行线段成比例,关键是根据平行线等分线段定理进行解答.举一反三【变式】如图,直线a∥b∥c,直线m、n与a、b、c分别交于点A、C、E、B、D、F,已知AC=4,CE=6,BD=3,则BF等于______________.【答案】7.5.类型二、平行线分线段成比例及其推论的应用3、如图,已知梯形ABCD中,AB∥DC,△AOB的面积等于9,△AOD的面积等于6,AB=7,求CD的长.【思路点拨】根据△AOB的面积等于9,△AOD的面积等于6,可知OB:OD的值,再根据平行线分线段成比例即可求解.【答案与解析】解: AB∥DC,∴22242DMAB, △AOB的面积等于9,△AOD的面积等于6,∴23DOBO,∴23CDDOABCO, AB=7,∴CD=143.【总结升华】主要考查了平行线分线段成比例和等高三角形的面积的比等于对应底边的比的性质,熟练掌握性质是解题的关键.举一反三【变式】如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,37ADAB,则EC的长是()A.4.5B.8C.10.5D.14【答案】解: DE∥BC,∴△ADE∽△ABC,∴ADAEABAC,∴6367AEACEC,解得:EC=8.故选:B.4、如图,直线l1∥l2∥l3,若AB=2,BC=3,DE=1,则EF的值为()A23B32C6D16【答案】B.【解析】解: 直线l1∥l2∥l3,∴ABDEACEF, AB=2,BC=3,DE=1,∴213EF,∴EF=32,故选B.【总结升华】本题考查平行线分线段成比例定理的应用,注意:一组平行线截两条直线,所截的对应线段成比例.举一反三【变式】如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么CF:CB等于()A.5:8B.3:8C.3:5D.2:5【答案】解: AD:DB=3:5,∴BD:AB=5:8, DE∥BC,∴CE:AC=BD:AB=5:8, EF∥AB,∴CF:CB=CE:AC=5:8.故选A.类型三、相似多边形的有关概念5、如图是一个由12个相似(形状相同,大小不同)的直角三角形所组成的图案,它是否有点像一个商标图案?你能否也用相似图形设计出几个美丽的图案?最好再给你设计的图案取一个名字.【思路点拨】相似图形是指形状相同的图形.根据相似图形进行变换可以形成一些美丽的图案.【答案与解析】解:由12个相似的直角三角形形成的图案很有创意,给人以美的享受,可以作为一个商标的图案.以...