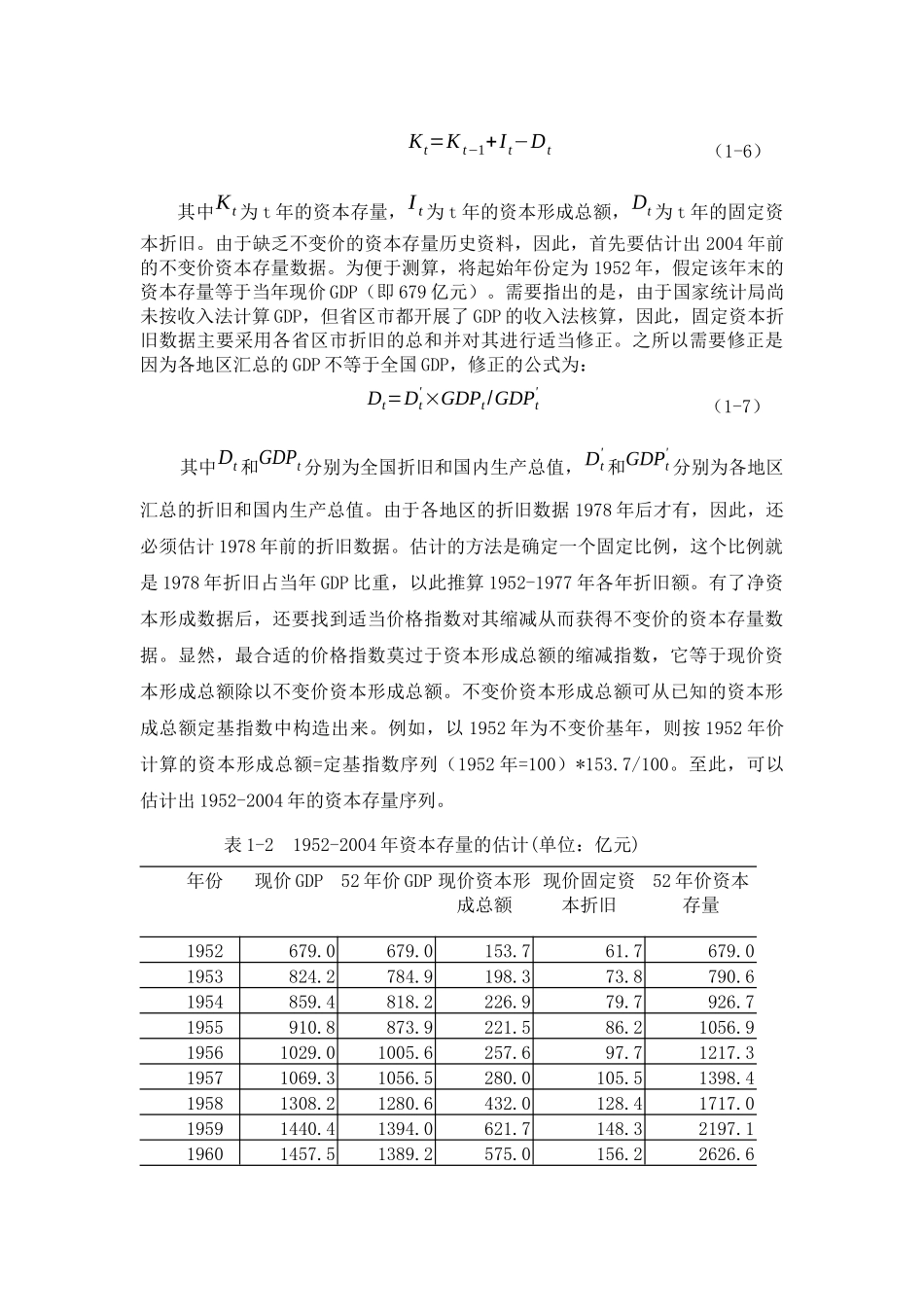
对我国生产率的分析和预测施发启一、传统生产函数模型索洛在1957年把道格拉斯、丁伯根的贡献和肯德里克(1956年)编制的国民生产帐户融成一体,提出了技术变化和总量生产函数,并表示为:Y=F(K,L,T)(1-1)式中Y是产出,K是资本投入,L是劳动投入,T是时间,在规模报酬不变的假设下,它反映了技术变化的效益理念。总量生产函数反映了产出和投入的依存关系。经数学推导,可得到索洛方程为:y.=skk.+sll.+ϕ(1-2)式中y.是产出增长率,k.是资本投入增长率,l.是劳动投入增长率,ϕ是生产率增长率;sk和sl分别为初始投入中资本和劳动的份额,因此sk+sl=1。在80年代以前,ϕ被定义为全要素生产率增长率(TFP),从生产者平衡理论的观点,ϕ意味着技术进步贡献量。(1-2)式反映了生产增长是由资本投入增长、劳动投入增长和生产率增长组成,如果把生产要素资本和劳动力叫做生产力,那么技术进步也是生产力。由(1-2)我们可以得出生产率增长率的度量方法是ϕ=y.−skk.−sll.(1-3)迄今为止,世界各国都在应用索洛增长方程来度量生产率增长率。虽然在索洛以后,有很多学者,如丹尼森、乔根森等,都做出很大努力,试图改进索洛方法,但由于国民核算体系不能满足数据的要求,他们提出的模型大都为理论探索,远没有像索洛方程那样实用。国外有很多研究报告经常用ΔlnY表示产出增长率y.,ΔlnK表示资本投入增长率k.,ΔlnL表示产出增长率l.,则(1-3)可写成:ϕ=ΔlnY−skΔlnK−slΔlnL(1-4)或ϕ=skΔln(Y/K)+slΔln(Y/L)(1-5)式中Δln(Y/K)是资本生产率增长率,Δln(Y/L)是劳动生产率增长率。因此,生产率增长率就等于资本生产率增长率与劳动生产率增长率的加权和。二、超越对数生产函数模型1973年,克里斯滕森、乔根森和劳伦斯提出“共轭对偶和超越对数生产函数”的计量方法,用于生产率的度量。他们所使用的基础模型仍是索洛总量生产函数Y=F(K,L,T),并假定它具有规模报酬不变的特征。定义YK=PKKY和YL=PLLY分别为资本投入报酬和劳动投入报酬占增加值的份额,PK和PL分别是资本投入价格和劳动投入价格,PKK和PLL分别是资本报酬和劳动报酬。生产者平衡的必要条件是每一投入的份额等于相应投入对产出的弹性,即YK=∂lnY(K,L,T)∂lnK和YL=∂lnY(K,L,T)∂lnL同时,生产率增长率YT是:YT=∂lnY(K,L,T)∂lnT。乔根森等提出的超越对数生产函数的计量模型是:Y=exp[α0+αKlnK+αLlnL+αTlnT+12βKKln2K+βKL(lnK)(lnL)+βKT(lnK)T+12βLLln2L+βLT(lnL)T+12βTTT2]式中α0、αK、αL、αT、βKK、βKL、βKT、βLL、βLT、βTT为待定参数,在规模报酬不变假设下,有下式成立:αK+αL=1βKK+βKL=0βKL+βLL=0βKK+βLL=0βKT+βLT=0在历史数据支持下,用计量经济方法无偏估计出以上各参数,并以此计算某一时期平均生产率增长率YT,即YT=∂lnY(K,L,T)∂lnT=αT+βKTlnK+βLTlnL+βTTT超越对数生产函数中,引进了二次项,能使生产率增长率的估计提高精度,但不适用于相邻两年或短周期的生产率度量,因此,目前大多数OECD国家(包括美国自己)在实证分析中仍使用索洛增长方程。超越对数生产函数模型在理论上或方法上有所创新,但还没有被广泛应用于实际工作。三、我国1953-2004年生产率测算结果及其变化分析在应用索洛模型测算我国生产率之前,有必要介绍一下资本投入、劳动投入的测算方法以及参数sk和sl的选择方法。(1)资本投入资本投入实质上就是资本存量,它等于上年资本存量加上本年固定资本形成减折旧,即Kt=Kt−1+It−Dt(1-6)其中Kt为t年的资本存量,It为t年的资本形成总额,Dt为t年的固定资本折旧。由于缺乏不变价的资本存量历史资料,因此,首先要估计出2004年前的不变价资本存量数据。为便于测算,将起始年份定为1952年,假定该年末的资本存量等于当年现价GDP(即679亿元)。需要指出的是,由于国家统计局尚未按收入法计算GDP,但省区市都开展了GDP的收入法核算,因此,固定资本折旧数据主要采用各省区市折旧的总和并对其进行适当修正。之所以需要修正是因为各地区汇总的GDP不等于全国GDP,修正的公式为:Dt=Dt'×GDPt/GDPt'(1-7)其中Dt和GDPt分别为全国折旧和国内生产总值,D...