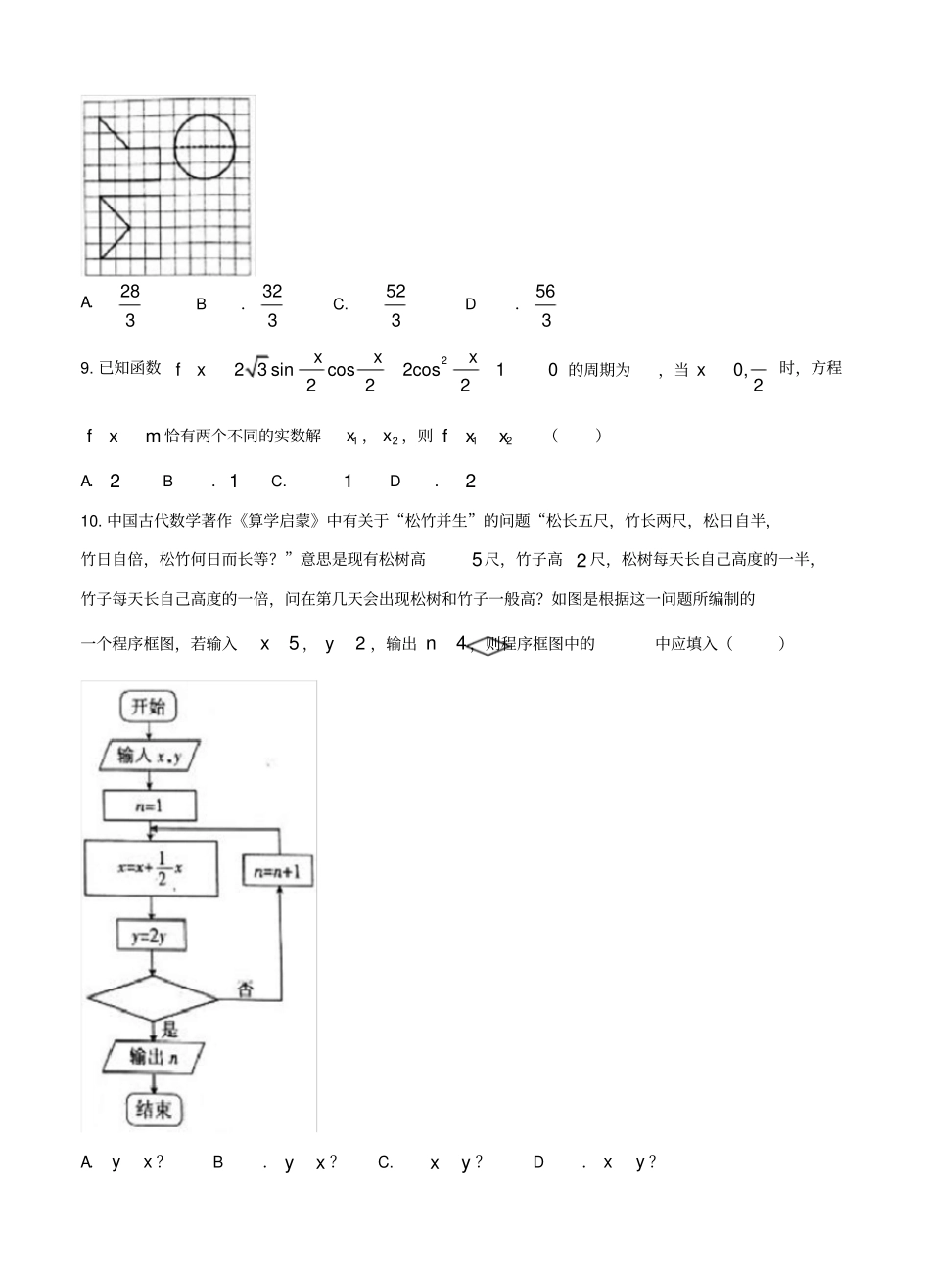
2018届山西省高三省际名校联考(三)文科数学第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合1,2,3,5,7A,26BxNx,全集UABU,则UBe()A.1,2,7B.1,7C.2,3,7D.2,72.已知平面向量1,2ABuuur,3,4ACuuur,则向量CBuuur的模是()A.2B.5C.22D.53.“0x”是“0x”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.问题“今有女子不善织布,逐日所织的布以同数递减,初日织五尺,末一日织一尺,计织三十日,问共织几何?”源自南北朝张邱建所著的《张邱建算经》,该问题的答案是()A.90尺B.93尺C.95尺D.97尺5.若函数22,0,,0xxfxgxx为奇函数,则2fg()A.2B.1C.0D.26.从装有大小材质完全相同的3个红球和3个黑球的不透明口袋中,随机摸出两个小球,则两个小球同色的概率是()A.23B.12C.25D.137.已知p为直线20xy上的点,过点p作圆22:1Oxy的切线,切点为M,N,若90MPNo,则这样的点p有()A.0个B.1个C.2个D.无数个8.某几何体的三视图如图所示,若图中小正方形的边长均为1,则该几何体的体积是()A.283B.323C.523D.5639.已知函数223sincos2cos10222xxxfx的周期为,当0,2x时,方程fxm恰有两个不同的实数解1x,2x,则12fxx()A.2B.1C.1D.210.中国古代数学著作《算学启蒙》中有关于“松竹并生”的问题“松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等?”意思是现有松树高5尺,竹子高2尺,松树每天长自己高度的一半,竹子每天长自己高度的一倍,问在第几天会出现松树和竹子一般高?如图是根据这一问题所编制的一个程序框图,若输入5x,2y,输出4n,则程序框图中的中应填入()A.yx?B.yx?C.xy?D.xy?11.已知函数2xfxexa,若曲线311,1yxxx上存在点00,xy使得00fyy,则实数a的取值范围是()A.3,93,eeUB.39,3eeC.329,6eeD.3,93,eeU12.在四面体ABCD中,23ABAC,6BC,AD底面ABC,DBC△的面积是6,若该四面体的顶点均在球O的表面上,则球O的表面积是()A.24B.32C.46D.49第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.复数z满足127izi,则复数z的共轭复数z.14.已知实数x,y满足约束条件20,350,1,xyxyy则212xyz的最大值是.15.是P为双曲线2222:1,0xyCabab上的点,1F,2F分别为C的左、右焦点,且212PFFF,1PF与y轴交于Q点,O为坐标原点,若四边形2OFPQ有内切圆,则C的离心率为.16.数列na满足1111,231nnnnnaaaaa是偶数,是奇数.,若134a,则数列na的前100项的和是.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.在ABC△中,内角A,B,C的对边分别为a,b,c,且coscos2coscBbCaA.(1)求A;(2)若2a,且ABC△的面积为3,求ABC△的周长.18.如图,三棱柱111ABCABC中,90BCAo,1AC平面1ABC.(1)证明:平面ABC平面11ACCA;(2)若2BCAC,11AAAC,求点1B到平面1ABC的距离.19.某大型商场去年国庆期间累计生成2万张购物单,从中随机抽出100张,对每单消费金额进行统计得到下表:消费金额(单位:元)0,200200,400400,600600,800800,1000购物单张数2525301010由于工作人员失误,后两栏数据已无法辨识,但当时记录表明,根据由以上数据绘制成的频率分布直方图所估计出的每单消费额的中位数与平均数恰好相等.用频率估计概率,完成下列问题:(1)估计去年国庆期间该商场累计生成的购物单中,单笔消费额超过800元的概率;(2)为鼓励顾客消费,该商场打算在今年国庆期间进行促销活动,凡单笔消费超过600元者,可抽奖一次,中一等奖、二等奖、三等奖的顾客可以分别获得价值500元、200元、100元的奖品.已知中奖率为100%,且一等奖、二等奖、三等奖的中奖率依次构成等比数列,其中一等奖的中奖率为121.若今年国庆期间该商场的购物单数量比去年同期增长5%,式预测商场今年国庆期间采办奖品的开销.20.已知抛物线2:4Exy的焦点为F,,0Pa为x轴上的点.(1)过点P作直线l与E相切,求切线l的方程;(2)如果存在过点F的直线'l与抛物线交于A,B两点,且直线PA与PB的倾斜角互补,求实数a的取值范围...