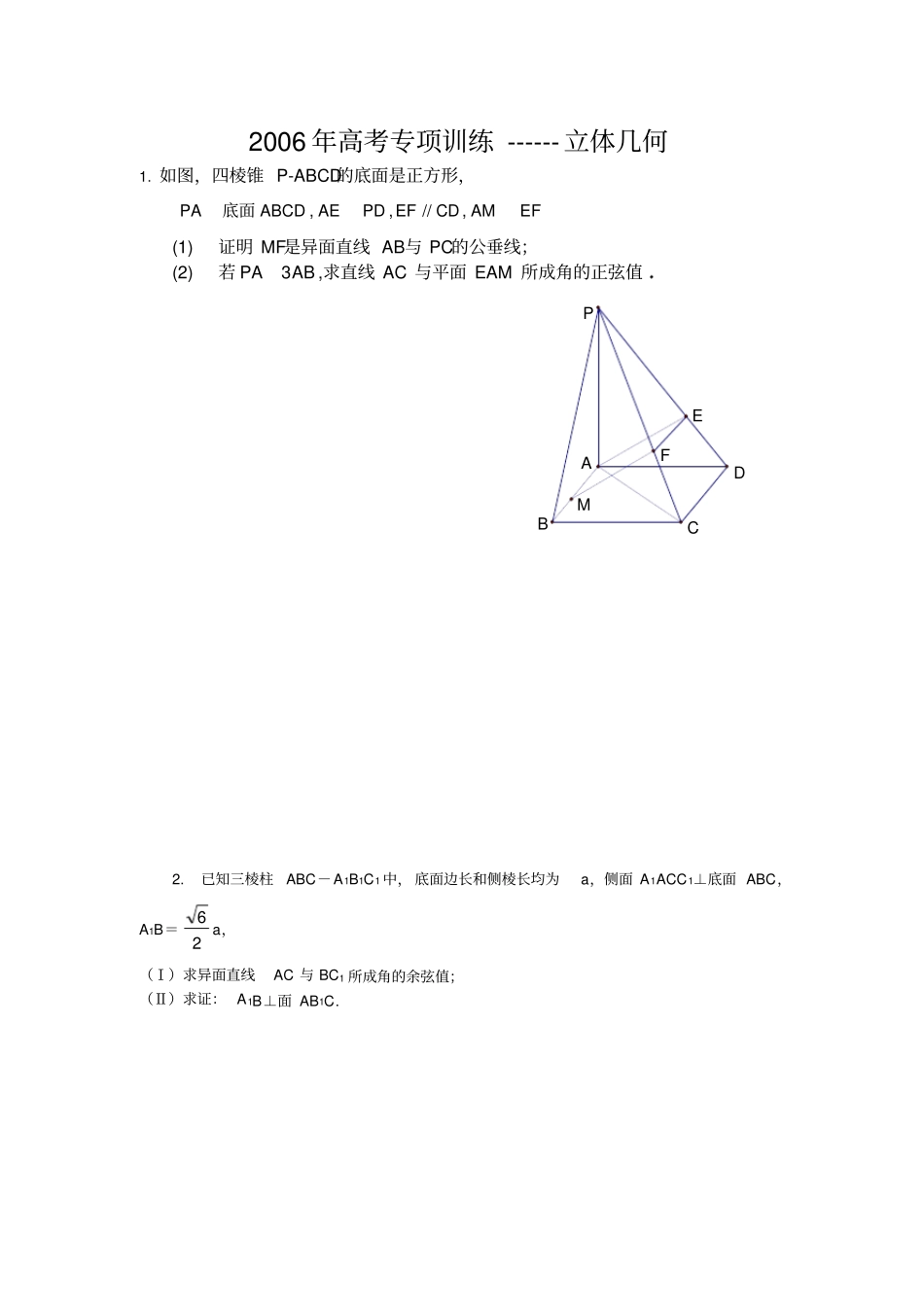
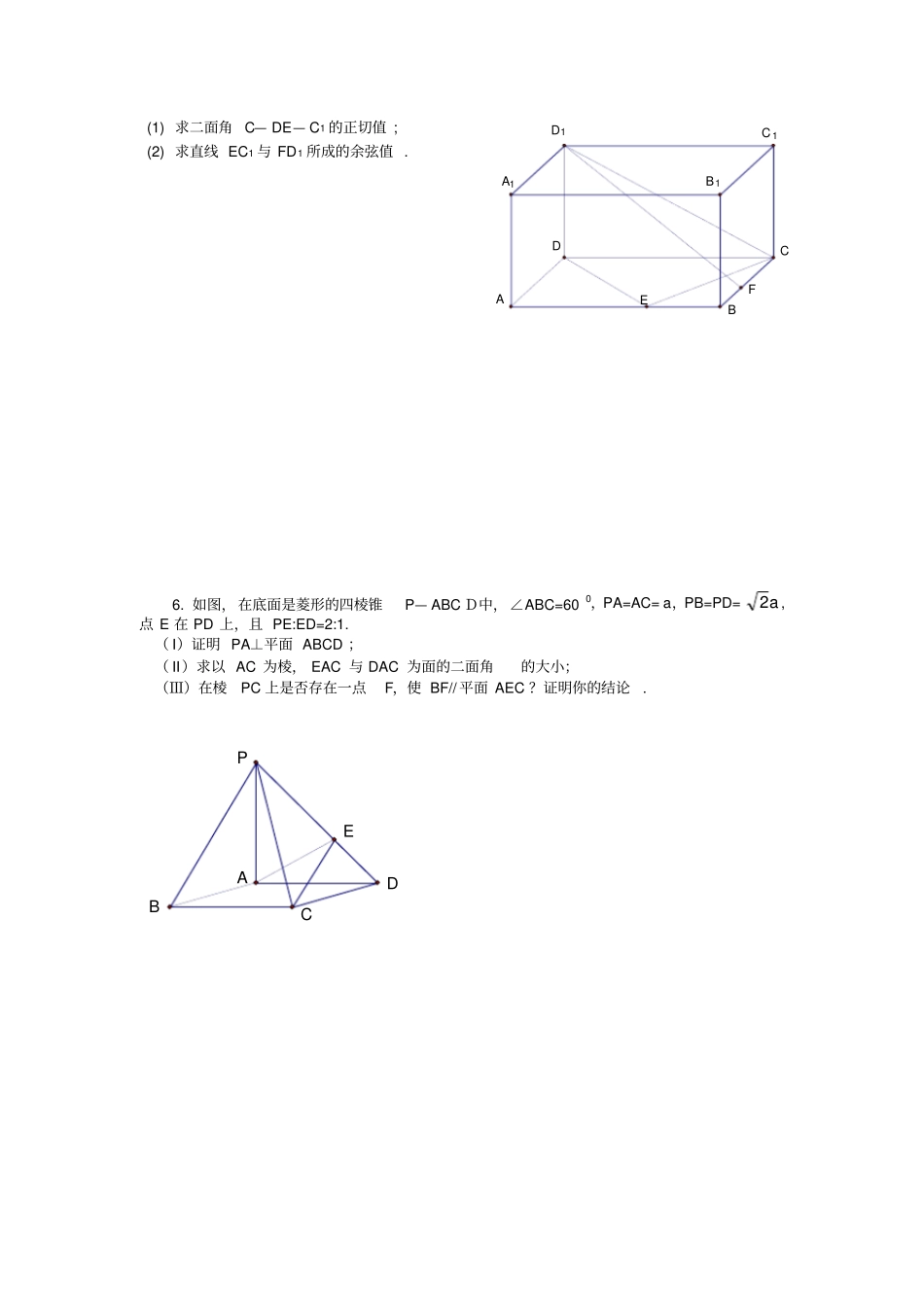
2006年高考专项训练------立体几何1.如图,四棱锥P-ABCD的底面是正方形,,,//,PAABCDAEPDEFCDAMEF底面(1)证明MF是异面直线AB与PC的公垂线;(2)若3PAAB,求直线AC与平面EAM所成角的正弦值2.已知三棱柱ABC-A1B1C1中,底面边长和侧棱长均为a,侧面A1ACC1⊥底面ABC,A1B=26a,(Ⅰ)求异面直线AC与BC1所成角的余弦值;(Ⅱ)求证:A1B⊥面AB1C.BCDAPMFE3.如图,四棱锥SABCD的底面是边长为1的正方形,SD垂直于底面ABCD,SB3DABSC(I)求证BCSC;(II)求面ASD与面BSC所成二面角的大小;(III)设棱SA的中点为M,求异面直线DM与SB所成角的大小4.在三棱锥S—ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=23,M、N分别为AB、SB的中点.(Ⅰ)证明:AC⊥SB;(Ⅱ)求二面角N—CM—B的大小;(Ⅲ)求点B到平面CMN的距离.5.如右下图,在长方体ABCD—A1B1C1D1中,已知AB=4,AD=3,AA1=2.E、F分别是线段AB、BC上的点,且EB=FB=1.(1)求二面角C—DE—C1的正切值;(2)求直线EC1与FD1所成的余弦值.6.如图,在底面是菱形的四棱锥P—ABCD中,∠ABC=600,PA=AC=a,PB=PD=a2,点E在PD上,且PE:ED=2:1.(I)证明PA⊥平面ABCD;(II)求以AC为棱,EAC与DAC为面的二面角的大小;(Ⅲ)在棱PC上是否存在一点F,使BF//平面AEC?证明你的结论.BCDAPED1C1B1CDBAA1EF7.在棱长为4的正方体ABCD-A1B1C1D1中,O是正方形A1B1C1D1的中心,点P在棱CC1上,且CC1=4CP.(Ⅰ)求直线AP与平面BCC1B1所成的角的大小(结果用反三角函数值表示);(Ⅱ)设O点在平面D1AP上的射影是H,求证:D1H⊥AP;(Ⅲ)求点P到平面ABD1的距离.8.如图,已知四棱锥P—ABCD,PB⊥AD侧面PAD为边长等于2的正三角形,底面ABCD为菱形,侧面PAD与底面ABCD所成的二面角为120°.(I)求点P到平面ABCD的距离,(II)求面APB与面CPB所成二面角的大小.·B1PACDA1C1D1BOH·9.如图,直三棱柱ABC-A1B1C1中,∠ACB=90o,AC=1,CB=2,侧棱AA1=1,侧面AA1B1B的两条对角线交点为D,B1C1的中点为M.(Ⅰ)求证:CD⊥平面BDM;(Ⅱ)求面B1BD与面CBD所成二面角的大小.10.三棱锥P-ABC中,侧面PAC与底面ABC垂直,PA=PB=PC=3.(1)求证AB⊥BC;(II)如果AB=BC=23,求AC与侧面PAC所成角的大小.ABCPABCDPABCDPFE11.如图,四棱锥P—ABCD中,底面ABCD为矩形,AB=8,AD=43,侧面PAD为等边三角形,并且与底面所成二面角为60°.(Ⅰ)求四棱锥P—ABCD的体积;(Ⅱ)证明PA⊥BD.12.已知四棱锥P—ABCD,底面ABCD是菱形,PDDAB,60平面ABCD,PD=AD,点E为AB中点,点F为PD中点.(1)证明平面PED⊥平面PAB;(2)求二面角P—AB—F的平面角的余弦值.13.如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F(1)证明PA//平面EDB;(2)证明PB⊥平面EFD;(3)求二面角C—PB—D的大小ABCDPEF14.如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=2,AF=1,M是线段EF的中点(Ⅰ)求证AM∥平面BDE;(Ⅱ)求二面角A—DF—B的大小;ABCDFEM参考答案1.解:(I)证明:因PA⊥底面,有PA⊥AB,又知AB⊥AD,故AB⊥面PAD,推得BA⊥AE,又AM∥CD∥EF,且AM=EF,证得AEFM是矩形,故AM⊥MF.又因AE⊥PD,AE⊥CD,故AE⊥面PCD,而MF∥AE,得MF⊥面PCD,故MF⊥PC,因此MF是AB与PC的公垂线.(II)解:连结BD交AC于O,连结BE,过O作BE的垂线OH,垂足H在BE上.易知PD⊥面MAE,故DE⊥BE,又OH⊥BE,故OH//DE,因此OH⊥面MAE.连结AH,则∠HAO是所要求的线AC与面NAE所成的角设AB=a,则PA=3a,aACAO2221.因Rt△ADE~Rt△PDA,故中从而在AHORtaEDOHaaaaPDADED.10221,10)3(2222.10520122102sinaaAOOHHAO2.解:(Ⅰ)105;(Ⅱ)略.3.解:(I)证明:如图1DABSC图1底面ABCD是正方形BCDCSD底面ABCDDC是SC在平面ABCD上的射影由三垂线定理得BCSC(II)解:SD底面ABCD,且ABCD为正方形可以把四棱锥SABCD补形为长方体ABCSABCD111,如图2面ASD与面BSC所成的二面角就是面ADSA1与面BCSA1所成的二面角,SCBCBCASSCAS,//11又SDAS1CSD为所求二面角的平面角在RtSCB中,由勾股定理得SC2在RtSDC中,由勾股定理得SD1CSD45即面ASD与面BSC所成的二面角为45C1CADBA1SB1图2BAD...