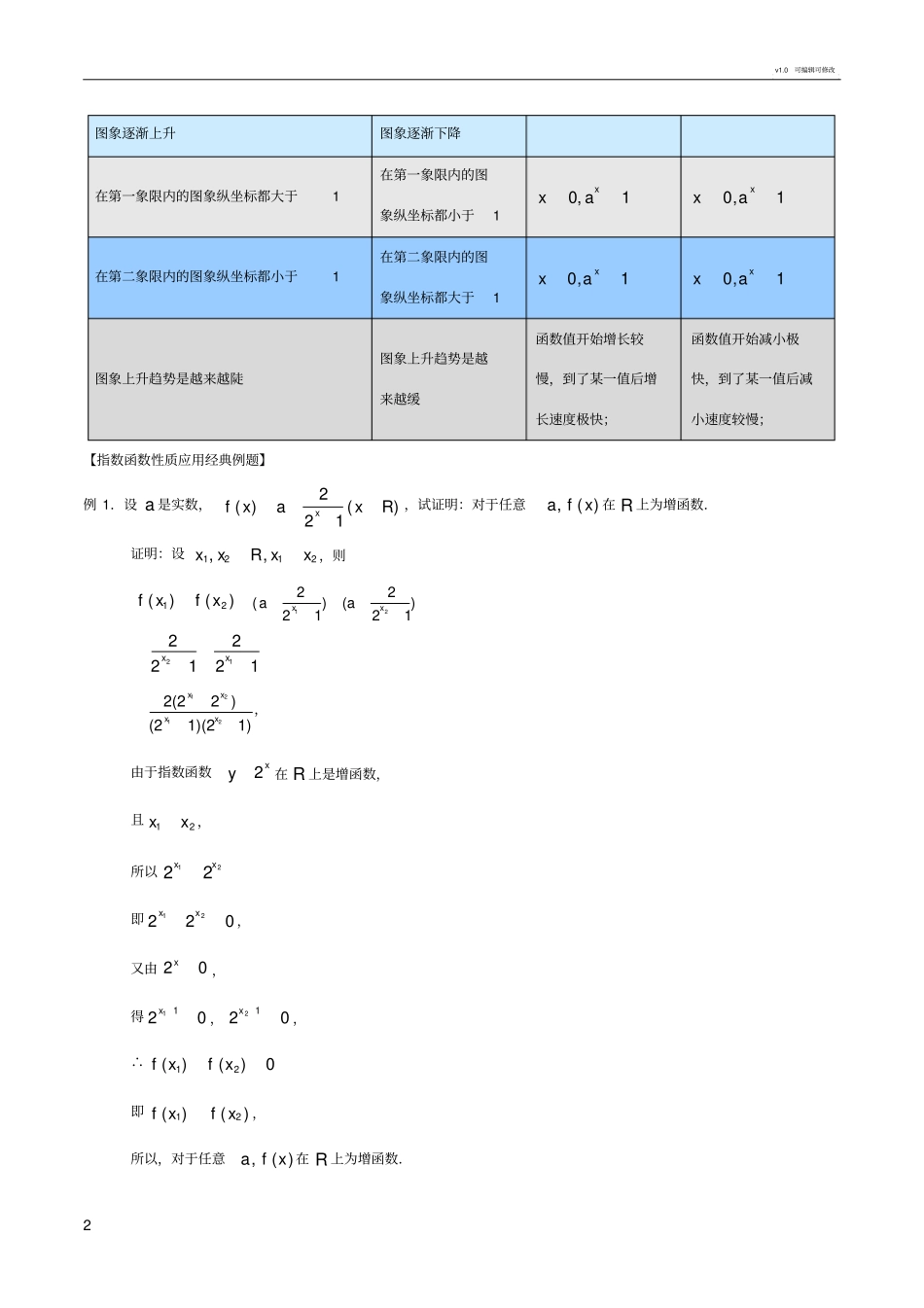
v1.0可编辑可修改1指数函数图像和性质及经典例题【基础知识回顾】一、指数公式部分有理指数幂的运算性质(1)ra·srraa),,0(Qsra;(2)rssraa)(),,0(Qsra;(3)srraaab)(),0,0(Qrba.正数的分数指数幂的意义)1,,,0(*nNnmaaanmnm)1,,,0(11*nNnmaaaanmnmnm二、指数函数1.指数函数的概念:一般地,函数)1a,0a(ayx且叫做指数函数,其中x是自变量,函数的定义域为R.2.指数函数的图象和性质1.在同一坐标系中画出下列函数的图象:(1)x)31(y(2)x)21(y(3)x2y(4)x3y(5)x5y图象特征函数性质1a1a01a1a0向x、y轴正负方向无限延伸函数的定义域为R图象关于原点和y轴不对称非奇非偶函数函数图象都在x轴上方函数的值域为R+函数图象都过定点(0,1)1a0自左向右看,自左向右看,增函数减函数v1.0可编辑可修改2图象逐渐上升图象逐渐下降在第一象限内的图象纵坐标都大于1在第一象限内的图象纵坐标都小于11a,0xx1a,0xx在第二象限内的图象纵坐标都小于1在第二象限内的图象纵坐标都大于11a,0xx1a,0xx图象上升趋势是越来越陡图象上升趋势是越来越缓函数值开始增长较慢,到了某一值后增长速度极快;函数值开始减小极快,到了某一值后减小速度较慢;【指数函数性质应用经典例题】例1.设a是实数,2()()21xfxaxR,试证明:对于任意,()afx在R上为增函数.证明:设1212,,xxRxx,则12()()fxfx1222()()2121xxaa21222121xx12122(22)(21)(21)xxxx,由于指数函数2xy在R上是增函数,且12xx,所以1222xx即12220xx,又由20x,得1120x,2120x,∴12()()0fxfx即12()()fxfx,所以,对于任意,()afx在R上为增函数.v1.0可编辑可修改3例2.已知函数2()1xxfxax(1)a,求证:(1)函数()fx在(1,)上为增函数;(2)方程()0fx没有负数根.证明:(1)设121xx,则1212121222()()11xxxxfxfxaaxx121212121212223()11(1)(1)xxxxxxxxaaaaxxxx,∵121xx,∴110x,210x,120xx,∴12123()0(1)(1)xxxx;∵121xx,且1a,∴12xxaa,∴120xxaa,∴12()()0fxfx,即12()()fxfx,∴函数()fx在(1,)上为增函数;(2)假设0x是方程()0fx的负数根,且01x,则000201xxax,即00000023(1)31111xxxaxxx,①当010x时,0011x,∴0331x,∴03121x,而由1a知01xa,∴①式不成立;当01x时,010x,∴0301x,∴03111x,而00xa,∴①式不成立.综上所述,方程()0fx没有负数根.v1.0可编辑可修改4针对性练习1.已知函数f(x)=ax+b的图象过点(1,3),且它的反函数f-1(x)的图象过(2,0)点,试确定f(x)的解析式.2.已知,32121xx求3212323xxxx的值.3.求函数y=3322xx的定义域、值域和单调区间.4.若函数y=a2x+b+1(a>0且a≠1,b为实数)的图象恒过定点(1,2),求b的值.5.设0≤x≤2,求函数y=1224221aaxx的最大值和最小值.v1.0可编辑可修改5针对性练习答案1解析:由已知f(1)=3,即a+b=3①又反函数f-1(x)的图象过(2,0)点即f(x)的图象过(0,2)点.即f(0)=2∴1+b=2∴b=1代入①可得a=2因此f(x)=2x+12解析:由,9)(22121xx可得x+x-1=7∵27)(32121xx∴23121212333xxxxxx=27∴2323xx=18,故原式=23解析:(1)定义域显然为(-∞,+∞).(2)uyxxxxfu3.4)1(423)(22是u的增函数,当x=1时,ymax=f(1)=81,而y=3223xx>0.∴]81,0(,3304即值域为u.(3)当x≤1时,u=f(x)为增函数,uy3是u的增函数,由x↑→u↑→y↑∴即原函数单调增区间为(-∞,1];当x>1时,u=f(x)为减函数,uy3是u的增函数,由x↑→u↓→y↓∴即原函数单调减区间为[1,+∞).v1.0可编辑可修改64解析:∵x=-2b时,y=a0+1=2∴y=a2x+b+1的图象恒过定点(-2b,2)∴-2b=1,即b=-25解析:设2x=t,∵0≤x≤2,∴1≤t≤4原式化为:y=21(t-a)2+1当a≤1时,ymin=942,2322max2aayaa;当1<a≤25时,ymin=1,ymax=2322aa;当a≥4时,ymin=232,9422max2aayaa.