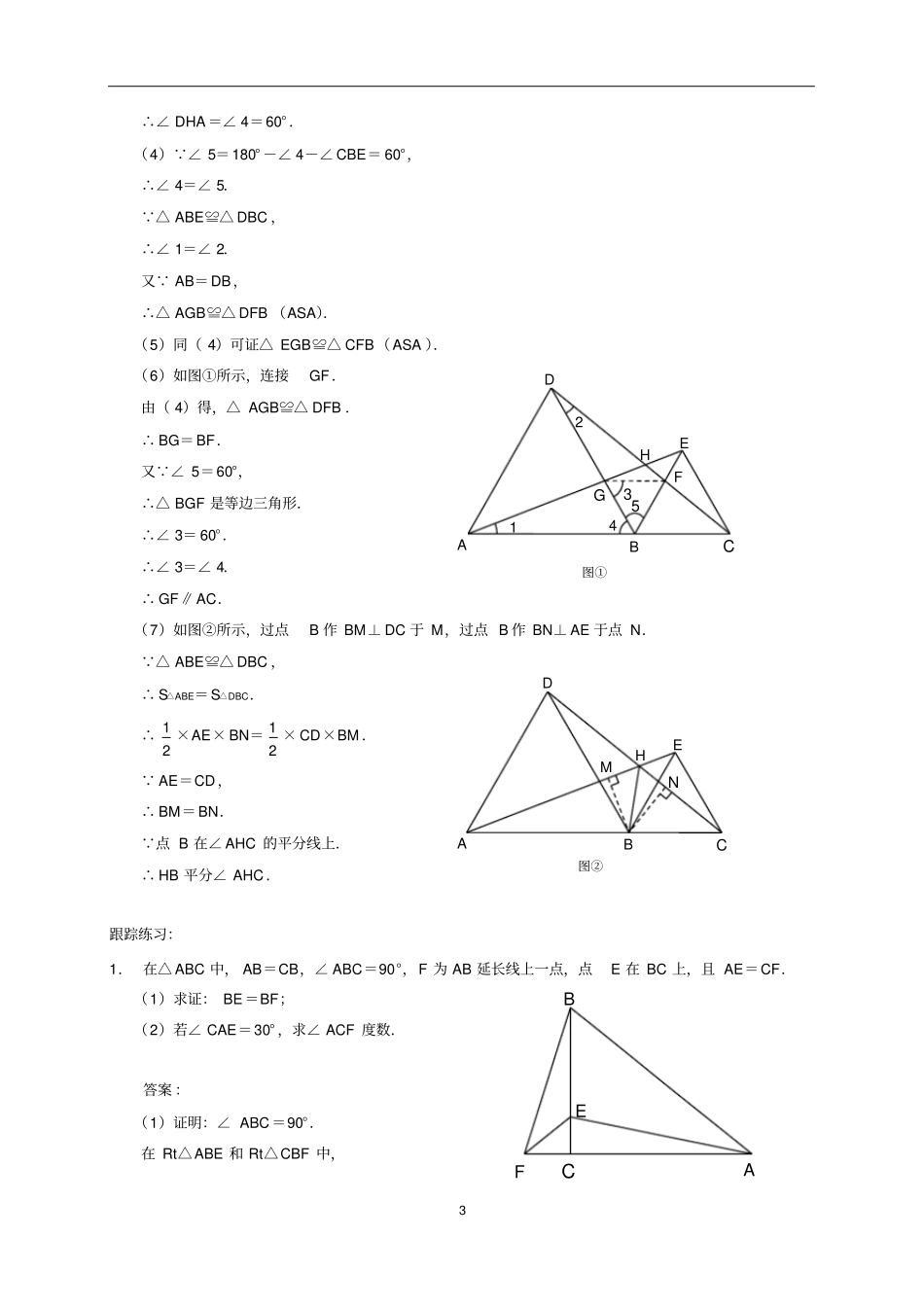
1手拉手模型模型手拉手如图,△ABC是等腰三角形、△ADE是等腰三角形,AB=AC,AD=AE,∠BAC=∠DAE=.结论:连接BD、CE,则有△BAD≌△CAE.模型分析如图①,∠BAD=∠BAC-∠DAC,∠CAE=∠DAE-∠DAC. ∠BAC=∠DAE=,∴∠BAD=∠CAE.在△BAD和△CAE中,ABACBADCAEADAE﹐﹐﹐图②、图③同理可证.(1)这个图形是由两个共顶点且顶角相等的等腰三角形构成.在相对位置变化的同时,始终存在一对全等三角形.(2)如果把小等腰三角形的腰长看作小手,大等腰三角形的腰长看作大手,两个等腰三角形有公共顶点,类似大手拉着小手,所以把这个模型称为手拉手模型.(3)手拉手模型常和旋转结合,在考试中作为几何综合题目出现.模型实例例1如图,△ADC与△EDG都为等腰直角三角形,连接AG、CE,相交于点H,问:(1)AG与CE是否相等?(2)AG与CE之间的夹角为多少度?CDEAB图①CDEAB图②CDEAB图③CDEGHAO2解答:(1)AG=CE.理由如下: ∠ADG=∠ADC+∠CDG,∠CDE=∠GDE+∠CDG,∠ADC=∠EDG=90°,∴∠ADG=∠CDE.在△ADG和△CDE中,ADCDADGCDEDGDE﹐﹐﹐∴△ADE≌△CDE.∴AG=CE.(2) △ADG≌△CDE,∴∠DAG=∠DCE. ∠COH=∠AOD,∴∠CHA=∠ADC=90°.∴AG与CE之间的夹角是90°.例2如图,在直线AB的同一侧作△ABD和△BCE,△ABD和△BCE都是等边三角形,连接AE、CD,二者交点为H.求证:(1)△ABE≌△DBC;(2)AE=DQ;(3)∠DHA=60°;(4)△AGB≌△DFB;(5)△EGB≌△CFB;(6)连接GF,GF∥AC;(7)连接HB,HB平分∠AHC.证明:(1)∠ABE=120°,∠CBD=120°,在△ABE和△DBC中,BABDABEDBCBEBC﹐﹐﹐∴△ABE≌△DBC.(2) △ABE≌△DBC,∴AE=DC.(3)△ABE≌△DBC,∴∠1=∠2.∴∠DGH=∠AGB.CDEFGHAB3∴∠DHA=∠4=60°.(4) ∠5=180°-∠4-∠CBE=60°,∴∠4=∠5. △ABE≌△DBC,∴∠1=∠2.又 AB=DB,∴△AGB≌△DFB(ASA).(5)同(4)可证△EGB≌△CFB(ASA).(6)如图①所示,连接GF.由(4)得,△AGB≌△DFB.∴BG=BF.又 ∠5=60°,∴△BGF是等边三角形.∴∠3=60°.∴∠3=∠4.∴GF∥AC.(7)如图②所示,过点B作BM⊥DC于M,过点B作BN⊥AE于点N. △ABE≌△DBC,∴S△ABE=S△DBC.∴12×AE×BN=12×CD×BM. AE=CD,∴BM=BN. 点B在∠AHC的平分线上.∴HB平分∠AHC.跟踪练习:1.在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.(1)求证:BE=BF;(2)若∠CAE=30°,求∠ACF度数.答案:(1)证明:∠ABC=90°.在Rt△ABE和Rt△CBF中,CDEFGHAB51234图①CDEHABNM图②CEFAB4CFAEABCB﹐﹐∴Rt△ABE≌Rt△CBF(HL).∴BE=BF.(2) AB=CB,∠ABC=90°,∴∠BAC=∠BCA=45°.∴∠CAE=30°.∴∠BAE=45°-30°=15°. Rt△ABE≌Rt△CBF,∴∠BCF=∠BAE=15°.∴∠ACF=∠BCF+∠BCA=15°+45°=60°.2.如图,△ABD与△BCE都为等边三角形,连接AE与CD,延长AE交CD于点H.求证:(1)AE=DC;(2)∠AHD=60°;(3)连接HB,HB平分∠AHC.答案:(1) ∠ABE=∠ABD-∠EBD,∠DBC=∠EBC-∠EBD,∠ABD=∠EBC=60°,∴∠ABE=∠DBC.在△ABE和△DBC中,ABDBABEDBCBEBC﹐﹐﹐∴△ABE≌△DBC.∴AE=DC.(2) △ABE≌△DBC,∴∠EAB=∠CDB.又 ∠OAB+∠OBA=∠ODH+∠OHD,∴∠AHD=∠ABD=60°.(3)过B作AH、DC的垂线,垂足分别为点M、N. △ABE≌△DBC,CDEHAB5∴S△ABE=S△DBC.即12AE·BM=12CD·BN.又 AE=CD,∴BM=BN.∴HB平分∠AHC.3.在线段AE同侧作等边△ABC和等边△CDE(∠ACE<120°),点P与点M分别是线段BE和AD的中点.求证:△CPM是等边三角形.答案:证明: △ABC和△CDE都是等边三角形,∴AC=BC,CD=CE.∴∠ACB=∠ECD=60°.∴∠BCE=∠ACD.∴△BCE≌△ACD.∴∠CBE=∠CAD,BE=AD.又 点P与点M分别是线段BE和AD的中点,∴BP=AM.在△BCP和△ACM中,BCACCBECADBPAM﹐﹐﹐∴△BCP≌△ACM.∴PC=MC,∠BCP=∠ACM.∴∠PCM=∠ACB=60°.∴△CPM是等边三角形.4.将等腰Rt△ABC和等腰Rt△ADE按图①方式...