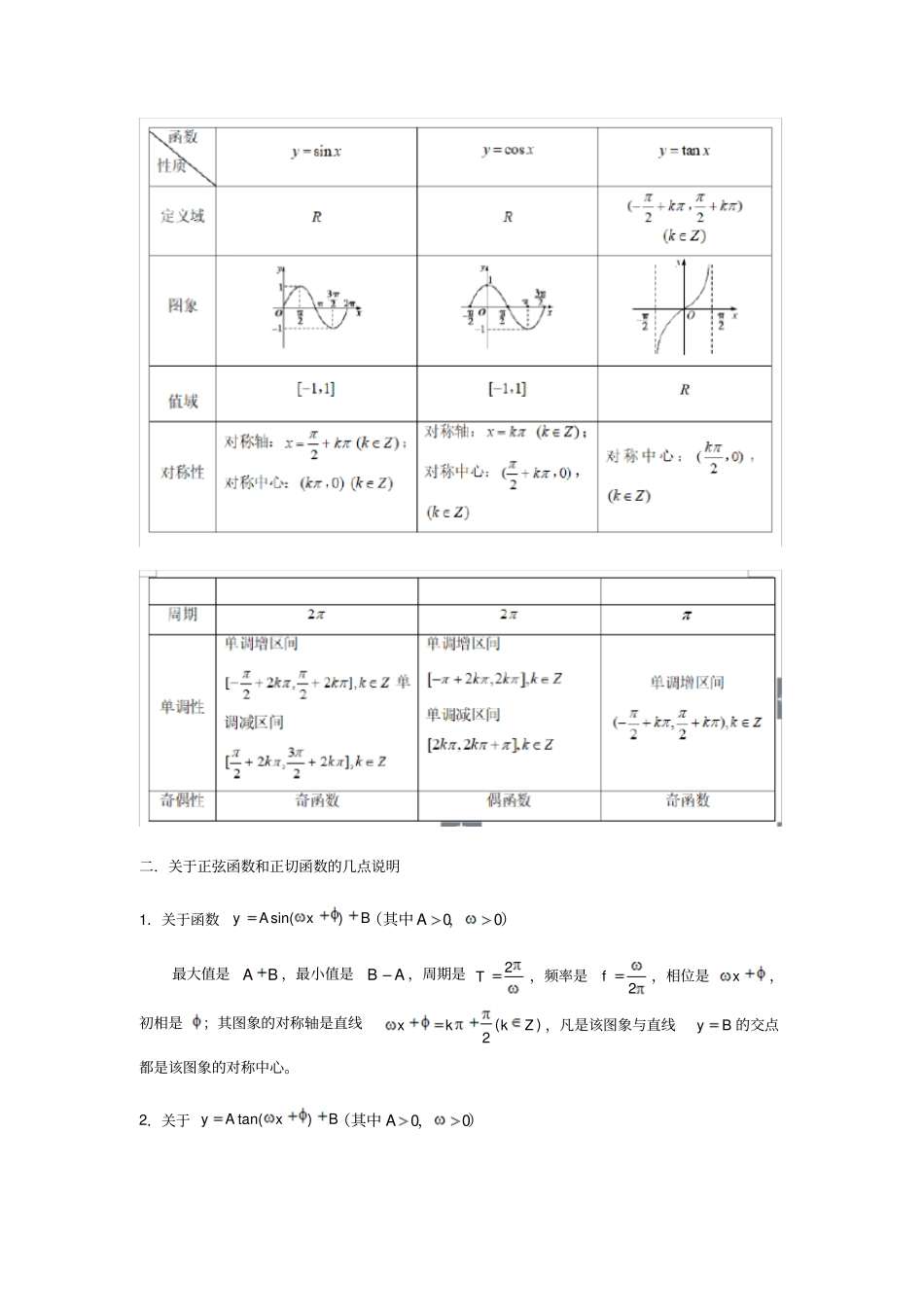
2017江苏高考复习三角函数的图像和性质(解析版)1/46一.三角函数图像和性质三角函数的图象和性质·知识图谱··知识精讲·二.关于正弦函数和正切函数的几点说明1.关于函数sin()yAxB00A(其中,)最大值是AB,最小值是BA,周期是2T,频率是2f,相位是x,初相是;其图象的对称轴是直线()2xkkZ,凡是该图象与直线yB的交点都是该图象的对称中心。2.关于tan()yAxB00A(其中,)2017江苏高考复习三角函数的图像和性质(解析版)3/46(1)正切函数图像的定义域为{|,}2xxkkZ,值域为全体实数R,不同于正弦函数和余弦函数定义域是全体实数R,值域是[11],.(2)关于tanfxx的最小正周期,最小正周期为T,而正弦和余弦函数的最小正周期为2T.(3)切记正切函数必须说是在定义域内单调递增,而不能说是在全体实数内单调递增.(4)正切函数图像的中心对称点是π(,0)(2kkZ),不同于正弦函数图像和余弦函数图像,对称轴只是与x轴的交点.(5)正切函数图像没有对称轴.一.考试范围与要求层次:二.命题方向1.三角函数图像的性质是高考考察的重点,主要出在单选题和解答题,尤其是解答题,是·三点剖析·历年考试必考点.2.热点是结合三角函数图像的性质与解三角形相关的题型.题模一:三角函数的定义域和值域(或最值)例1.1.1函数f(x)=cos2x+2sinx(x∈[0,54])的值域是____.例1.1.2求12log2sin1yx定义域例1.1.3求2logsinyx定义域题模二:三角函数的周期性与奇偶性例1.2.1函数y=sin(32+x)是()A.奇函数B.偶函数C.既是奇函数又是偶函数D.非奇非偶函数例1.2.2若函数()sin()3sin()44fxaxx是偶函数,则实数a的值为__________.·题模精选·2017江苏高考复习三角函数的图像和性质(解析版)5/46例1.2.3将函数f(x)=sin(12x-3)的图象沿x轴向右平移a(a>0)个单位,所得图象关于y轴对称,则a的最小值为()A.6B.3C.56D.53题模三:三角函数的单调性例1.3.1函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<2)的部分图象如图所示,则()A.函数f(x)在区间[0,2]上单调递增B.函数f(x)在区间[0,2]上单调递减C.函数f(x)在区间[0,2]上的最小值为﹣2D.函数f(x)在区间[0,2]上的最小值为﹣1例1.3.2同时具有性质“①最小正周期是π,②图象关于x=3对称,③在[,]63上是增函数”的一个函数是()A.sin(2)6yxB.cos(2)3yxC.sin()26xyD.cos(2)6yx例1.3.3若函数f(x)=sin(ωx+φ),其中0,||,2xR,两相邻对称轴的距离为2,()6f为最大值,则函数f(x)在区间[0,π]上的单调增区间为()A.[0,]6B.2[,]3C.[0,]6和[,]3D.[0,]6和2[,]3随练1.1求12sinyx定义域随练1.2求函数1sin2log1xy的定义域.随练1.3设()12sinfxx,()fx的定义域为__________.随练1.4函数y=sin(2x+φ)的图象沿x轴向左平移8个单位后,得到一个偶函数的图象,则φ的一个可能的值为()A.34B.4C.0D.-4随练1.5下列函数中,以2为最小正周期的偶函数是()A.y=sin2x+cos2xB.y=sin2xcos2xC.y=cos(4x+2)D.y=sin22x-cos22x随练1.6设f(x)=sin(ωx+φ),其中ω>0,则f(x)是偶函数的充要条件是()A.f(0)=1B.f(0)=0C.f′(0)=1D.f′(0)=0随练1.7已知ω∈N+,函数f(x)=sin(ωx+4)在(6,3)上单调递减,则ω=.·随堂练习·2017江苏高考复习三角函数的图像和性质(解析版)7/46随练1.8已知函数f(x)=4cosωx?sin(ωx+4)(ω>0)的最小正周期为π.(1)求ω的值;(2)讨论f(x)在区间[0,2]上的单调性.随练1.9已知函数f(x)=Asin(ωx+φ)(x∈R,ω>0,0<φ<2)的部分图象如图所示.(Ⅰ)求函数f(x)的解析式;(Ⅱ)求函数g(x)=f(x-12)-f(x+12)的单调递增区间.一.图像的变换1.由sin()yAxB的图象变换出sin()yAxB的图象的方法:图像伸缩为三角函数的图象变换·知识精讲·原来的1.2.由sinyAxB的图象变换出sin()yAxB的图象的方法:图像向左平移个单位.二.根据函数图像求解析式如何确定sin()yAx中的A,和1.根据最高点和最低点求A;2.根据周期,通过2T求;3.带入图像中的一个点求.2017江苏高考复习三角函数的图像和性质(解析版)9/46一.考试范围与要求层...