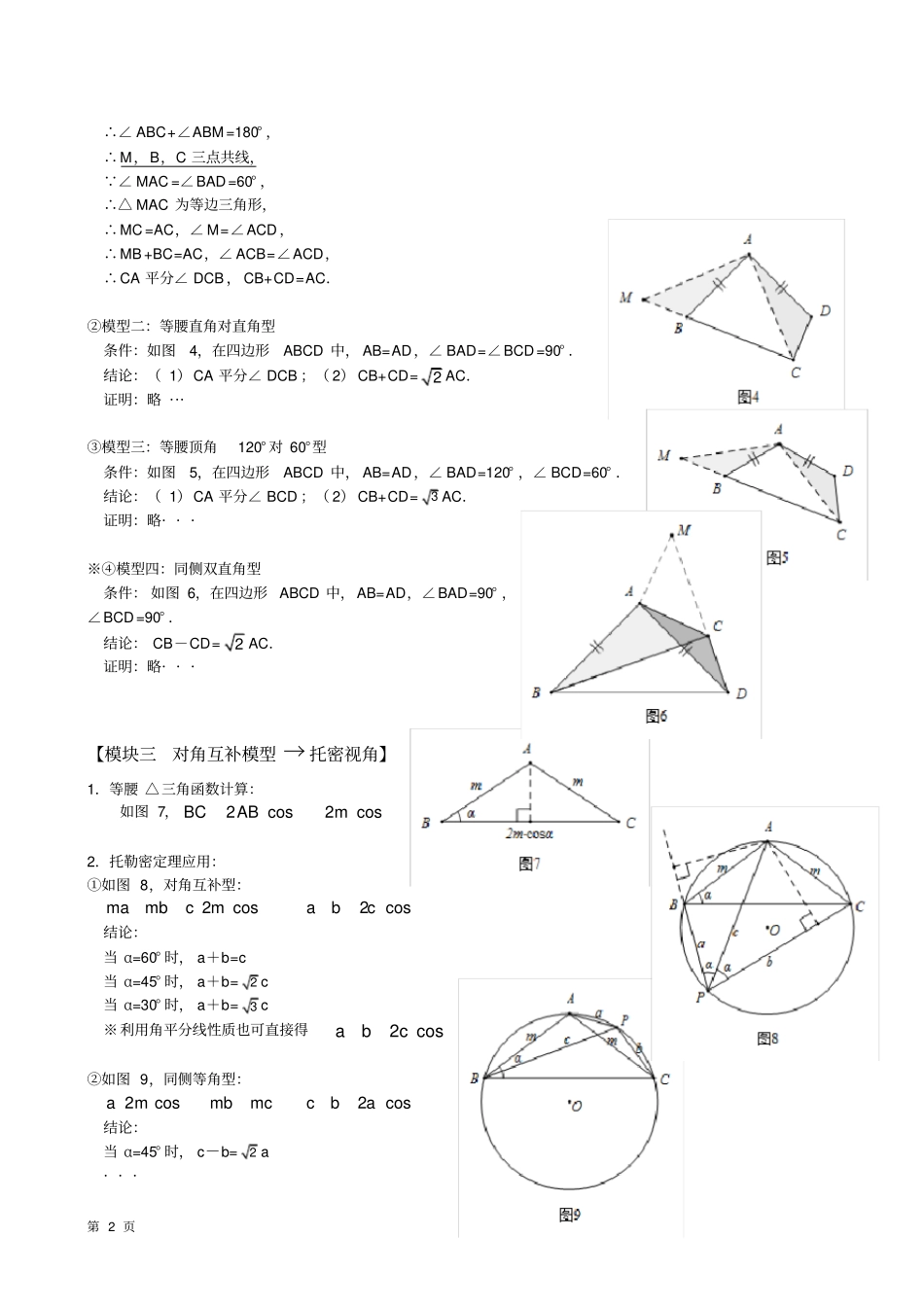
第1页托勒密定理、婆氏定理——圆中基本模型专题(二)【教学重难点】1.圆中托勒密定理;对角互补模型:旋转视角、托勒密视角2.婆罗摩笈多定理3.例题探究【模块一圆中托勒密定理】古希腊最伟大的天文学家,数学家、天文学家伊巴谷(约公元前190年-公元前125年),最早提出了,圆内接四边形两对对边乘积的和等于两条对角线的乘积,后称托勒密定理.古罗马著名的天文学家、光学家克罗狄斯·托勒密(约90年-168年),从伊巴谷的书中将其摘出并完善.托勒密定理实质上是关于共圆性的基本性质,故从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式.1.基本图形与结论:如图1,当A、B、C、D四点共圆,则AC×BD=AB×DC+AD×BC.2.简单证明:在线段BD上取一点E,连AE,使∠AEB=∠ADC,易得△AEB∽△ADC,ACCDACBEABCDABBE①旋转一拖二得△ABC∽△AED,ACBCACDEBCADADDE②由①+②得:AC×(BE+DE)=AC×BD=AB×DC+AD×BC.3.模型识别:具体情境中出现四点共圆,且四点构成的四边形边长、对角线长信息较多,可以尝试用托勒密定理进行计算.※4.广义托勒密定理:对于任意凸四边形ABCD,则有AC×BD≤AB×DC+AD×BC.证明从略···【模块二对角互补模型→旋转视角】1.基本图形与模型识别:如图2,对角互补且一组邻边相等...........的四边形,可通过旋转变换将四边形转化为等腰三角形(等腰思旋转).2.四类常见对角互补模型:①模型一:等边60°对120°型条件:如图3,在四边形ABCD中,AB=AD,∠BAD=60°,∠BCD=120°结论:(1)CA平分∠BCD;(2)BC+CD=AC.证明:证明:如图,将△ACD绕点A逆时针旋转60°至△AMB,使AD,AB重合,则△ACD≌△AMB,∴∠ADC=∠ABM,AC=AM,CD=BM,∠ACD=∠M, ∠BAD=60°,∠BCD=120°,∴∠ABC+∠ADC=180°,第2页∴∠ABC+∠ABM=180°,∴M,B,C三点共线, ∠MAC=∠BAD=60°,∴△MAC为等边三角形,∴MC=AC,∠M=∠ACD,∴MB+BC=AC,∠ACB=∠ACD,∴CA平分∠DCB,CB+CD=AC.②模型二:等腰直角对直角型条件:如图4,在四边形ABCD中,AB=AD,∠BAD=∠BCD=90°.结论:(1)CA平分∠DCB;(2)CB+CD=2AC.证明:略···③模型三:等腰顶角120°对60°型条件:如图5,在四边形ABCD中,AB=AD,∠BAD=120°,∠BCD=60°.结论:(1)CA平分∠BCD;(2)CB+CD=3AC.证明:略···※④模型四:同侧双直角型条件:如图6,在四边形ABCD中,AB=AD,∠BAD=90°,∠BCD=90°.结论:CB-CD=2AC.证明:略···【模块三对角互补模型→托密视角】1.等腰△三角函数计算:如图7,2cos2cosBCABm2.托勒密定理应用:①如图8,对角互补型:2cos2cosmambcmabc结论:当α=60°时,a+b=c当α=45°时,a+b=2c当α=30°时,a+b=3c※利用角平分线性质也可直接得2cosabc②如图9,同侧等角型:2cos2cosammbmccba结论:当α=45°时,c-b=2a···第3页【模块四婆罗摩笈多定理】婆罗摩笈多(约公元598-约660年)是一位印度数学家和天文学家,他出身于古印度的婆罗门种姓,婆罗门掌管着解释和预言天象的权力,掌握着天文学知识,以及测量和计算天体运行的工具——数学.婆罗摩笈多著有两部关于数学和天文学的书籍,他的一些数学成就在世界数学史上有较高的地位,他的负数及加减法运算仅晚于中国九章算术,而他的负数乘除法法则在全世界都是领先的.婆罗摩笈多还提出了著名的婆罗摩笈多定理,简称“婆氏定理”.若圆内接四边形的对角线相互垂直,则垂直于一边且过对角线交点的直线将平分对边.1.简单证明:已知:如图,四边形ABCD内接于圆O,对角线AC⊥BD于点M,ME⊥BC于点E,延长EM交CD于点F,求证:F是AD中点.证明: AC⊥BD,ME⊥BC∴∠CBD=∠CME ∠CBD=∠CAD,∠CME=∠AMF∴∠CAD=∠AMF∴AF=MF ∠AMD=90°,同时∠MAD+∠MDA=90°∴∠FMD=∠FDM∴MF=DF,∴AF=DF即F是AD中点.2.婆罗摩笈多逆定理请你阅读婆罗摩笈多定理的证明过程,试证明婆罗摩笈多逆定理:(1)如图1,四边形ABCD内接于圆O,对角线AC⊥BD于点M,F为AD中点,连接FM并延长交BC于点E,求证:ME⊥BC.(2)如图2,△ABC内接于圆O,∠B=30°,∠ACB=45°,AB=2,点D在圆...