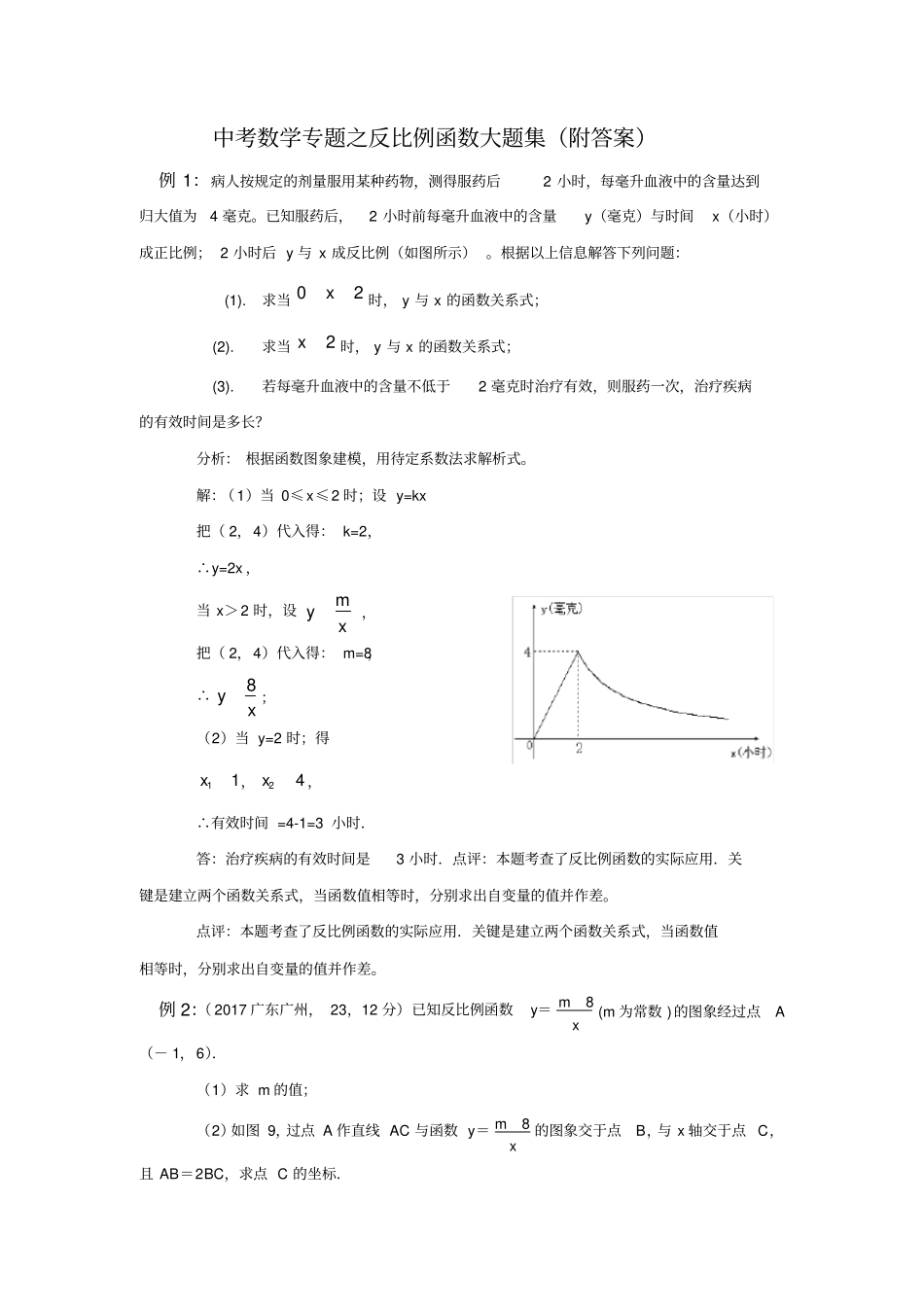
中考数学专题之反比例函数大题集(附答案)例1:病人按规定的剂量服用某种药物,测得服药后2小时,每毫升血液中的含量达到归大值为4毫克。已知服药后,2小时前每毫升血液中的含量y(毫克)与时间x(小时)成正比例;2小时后y与x成反比例(如图所示)。根据以上信息解答下列问题:(1).求当时,y与x的函数关系式;(2).求当时,y与x的函数关系式;(3).若每毫升血液中的含量不低于2毫克时治疗有效,则服药一次,治疗疾病的有效时间是多长?分析:根据函数图象建模,用待定系数法求解析式。解:(1)当0≤x≤2时;设y=kx把(2,4)代入得:k=2,∴y=2x,当x>2时,设myx,把(2,4)代入得:m=8,∴8yx;(2)当y=2时;得11x,24x,∴有效时间=4-1=3小时.答:治疗疾病的有效时间是3小时.点评:本题考查了反比例函数的实际应用.关键是建立两个函数关系式,当函数值相等时,分别求出自变量的值并作差。点评:本题考查了反比例函数的实际应用.关键是建立两个函数关系式,当函数值相等时,分别求出自变量的值并作差。例2:(2017广东广州,23,12分)已知反比例函数y=8mx(m为常数)的图象经过点A(-1,6).(1)求m的值;(2)如图9,过点A作直线AC与函数y=8mx的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.20x2x分析:(1)将A点坐标代入反比例函数解析式即可得到一个关于m的一元一次方程,求出m的值;(2)分别过点A、B作x轴的垂线,垂足分别为点D、E,则△CBE△△CAD,运用相似三角形知识求出CE的长即可求出点C的横坐标.解:(1)△图像过点A(-1,6),861m.△m-8-1=6(2)分别过点A、B作x轴的垂线,垂足分别为点D、E,由题意得,AD=6,OD=1,易知,AD△BE,△△CBE△△CAD,△CBBECAAD.△AB=2BC,△13CBCA△136BE,△BE=2.即点B的纵坐标为2当y=2时,x=-3,易知:直线AB为y=2x+8,△C(-4,0)涉及知识点:反比例函数点评:由于今年来各地中考题不断降低难度,中考考查知识点有向低年级平移的趋势,反比例函数出现在解答题中的频数越来约多.例3:已知:如图,正比例函数y=ax的图象与反比例函数xky的图象交于点A(3,2).(1)试确定上述正比例函数和反比例函数的表达式;(2)根据图象回答,在第一象限内,当x取何值时,反比例函数的值大于正比例函数的值;BAOCyxBAOCyxDE(3)M(m,n)是反比例函数图象上的一动点,其中0<m<3,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交于点C,交直线MB于点D.当四边形OADM的面积为6时,请判断线段BM与DM的大小关系,并说明理由.分析:(1)由点A为正比例与反比例函数图象的交点,将A点坐标代入正比例函数y=ax中,求出a的值,确定出正比例函数的解析式,将A点坐标代入反比例函数xky中,求出k的值,确定出反比例函数的解析式;(2)由A的横坐标及函数图象可得出反比例函数的值大于该正比例函数的值时,x的范围范围;(3)过M作MQ垂直于x轴,由M为反比例函数上的点,将M的坐标代入反比例函数解析式中求出mn=6,同时由三个角的为直角的四边形为矩形得到四边形BOCD为矩形,根据矩形的对边相等可得出BO=DC,又BMQO为矩形,得到MQ=BO,由M的纵坐标为n,得到MQ=BO=DC=n,横坐标为m,得到BM=m,由A的坐标得出AC及OC的长,四边形OADM的面积=矩形BOCD的面积-三角形BMO的面积-三角形AOC的面积,利用矩形及三角形的面积公式分别表示出各自的面积,将mn=6及四边形OADM的面积为6代入,得出关于n的方程,求出方程的解得到n的值,进而求出m的值,即可确定出M的坐标,就可判断线段BM与DM的大小关系了.BM=32,MD=3-32=32所以BM=MD例4:(2018广州中考25)如图,在平面直角坐标系中,点O为坐标原点,正方形OABC的边OA、OC分别在x轴、y轴上,点B的坐标为(2,2),反比例函数0,0kyxkx的图象经过线段BC的中点D。(1)求k的值;(2)若点P(x,y)在该反比例函数的图象上运动(不与点D重合),过点P作PR⊥y轴于点R,作PQ⊥BC所在直线于点Q,记四边形CQPR的面积为S,求S关于x的解析式并写出x的取值范围。yxODCBA