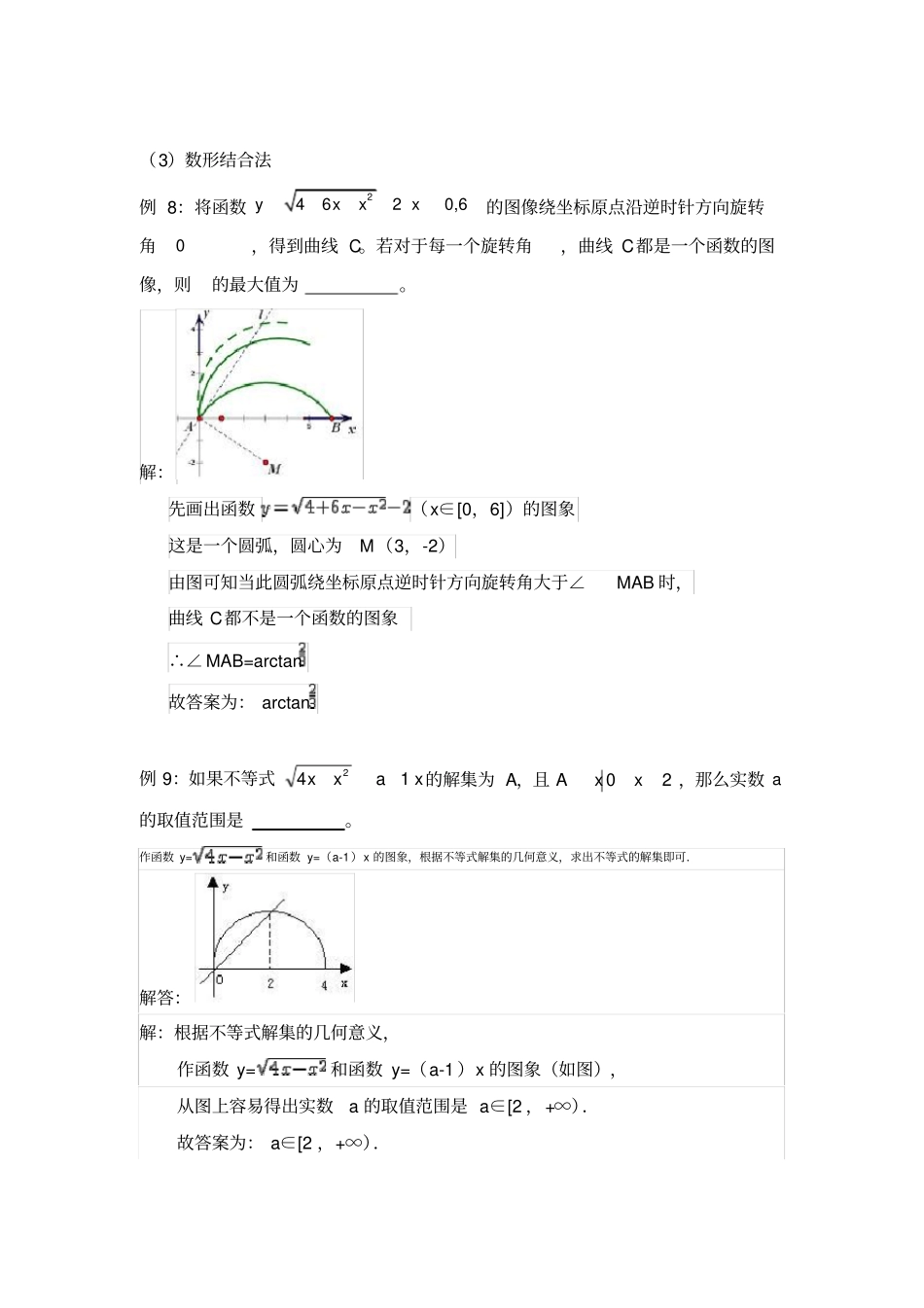
专题1:解填空题和选择题的原则及方法【解填空题的原则及方法】(1)直接法:例1:若复数z满足iiz11(i是虚数单位),则其共轭复数z=i。例2:已知数列nnba,都是等差数列,4,011ba,用',kkSS分别表示数列nnba,的前k项和(k是正整数),若0'kkSS,则kkba的值为5。解:根据等差数列求和公式,得Sk=(a1+ak),S=(b1+bk), Sk+Sk′=0,∴(a1+ak)+(b1+bk)=0, ,∴a1+ak+b1+bk=0, a1=-1,b1=-4,∴ak+bk=-(a1+b1)=4.故答案为:4.(2)特殊化法:例3:已知函数xxxftansin,项数为27的等差数列na满足2,2na,且公差0d,若0...2721afafaf,则当k=14时,0kaf。解:因为函数f(x)=sinx+tanx是奇函数,所以图象关于原点对称,图象过原点.而等差数列{an}有27项,an∈().若f(a1)+f(a2)+f(a3)+⋯+f(a27)=0,则必有f(a14)=0,所以k=14.答案为:14例4:在中,角A、B、C所对的边分别为cba,,,若cba,,成等差数列,则CACAcoscos1coscos=。解: a、b、c成等差数列,不妨令a=3,b=4,c=5则△ABC为直角三角形则cosA=,cosC=0∴==故答案为:例5:过抛物线2axy0a的焦点F作一直线交抛物线于P、Q两点,若线段PF、FQ的长分别为qp,,则qp11=。解:设PQ的斜率k=0,因抛物线焦点坐标为(0,),把直线方程y=代入抛物线方程得x=±,∴PF=FQ=,从而=2a+2a=4a,故答案为:4a.例6:设1ba,则bababbalog,log,log的大小关系是logloglogbaababb例7:椭圆92x+42y=1的焦点为F1、F2,点P为其上的动点,当∠F1PF2为钝角时,点P横坐标的取值范围是。解:设p(x,y),则,且∠F1PF2是钝角?x2+5+y2<10.故答案为:.(3)数形结合法例8:将函数24620,6yxxx的图像绕坐标原点沿逆时针方向旋转角0,得到曲线C。若对于每一个旋转角,曲线C都是一个函数的图像,则的最大值为。解:先画出函数(x∈[0,6])的图象这是一个圆弧,圆心为M(3,-2)由图可知当此圆弧绕坐标原点逆时针方向旋转角大于∠MAB时,曲线C都不是一个函数的图象∴∠MAB=arctan故答案为:arctan例9:如果不等式xaxx142的解集为A,且20xxA,那么实数a的取值范围是。作函数y=和函数y=(a-1)x的图象,根据不等式解集的几何意义,求出不等式的解集即可.解答:解:根据不等式解集的几何意义,作函数y=和函数y=(a-1)x的图象(如图),从图上容易得出实数a的取值范围是a∈[2,+∞).故答案为:a∈[2,+∞).例10:若关于x的方程212xkx有两个不等实根,则实数k的取值范围是3(,0]3。解:21yx与2ykx有两个交点时k的取值范围(4)等价转化法例11:已知24122xxx,则函数xxy22的值域是2553[,]162。例12:不论k为实数,直线1kxy与曲线0422222aaaxyx恒有交点,则实数a的取值范围是。解:直线y=kx+1恒过(0,1)点,与曲线x2+y2-2ax+a2-2a-4=0恒有交点,必须定点在圆上或圆内,即:所以,-1≤a≤3故答案为:-1≤a≤3.例13:函数xxy3214的单调递减区间为13[,3]8。解:定义域为1[,3]4,将函数转化为221144133yxx在113[,)48上单调递增,在13[,3]8【解选择题的原则及方法】(1)排除法例14:已知函数f(x)=2mx2-2(4-m)x+1,g(x)=mx,若对于任一实数x,f(x)与g(x)至少有一个为正数,则实数m的取值范围是()A.(0,2)B.(0,8)C.(2,8)D.(-∞,0)解:当m≤0时,显然不成立当m>0时,因f(0)=1>0当,即0<m≤4时结论显然成立;当,时只要△=4(4-m)2-8m=4(m-8)(m-2)<0即可,即4<m<8则0<m<8故选B.(2)设定特殊数值或条件例15:设F为抛物线xy42的焦点,A、B、C为该抛物线上三点,若0FCFBFA,则FCFBFA()。A、9;B、6;C、4;D、3;解:B(3)归纳法(找规律)例16:双曲线222yx的左、右焦点分别为21FF,点...3,2,1,nyxPnn在其右支上,且满足2121121,FFFPFPFPnn,则2008x的值为()。A、24016;B、24015;C、4016;D、4015;解: Pn+1点在双曲线x2-y2=2右支上,∴|Pn+1F1|-|Pn+1F2|=2又 |Pn+1F2|=|PnF1|,∴|Pn+1F1|-|PnF1|=2∴数列{PnF1|}为等差数列,公差为2 P1F2⊥F1F2,∴|P1F2|=,则|P1F1|=3∴|P2008F1|=|P1F1|+2007×2=3+2007×2=4017 双曲线x2-y2=2的左准线方程为x=-1,离心率为,设P2008到左准线距离...