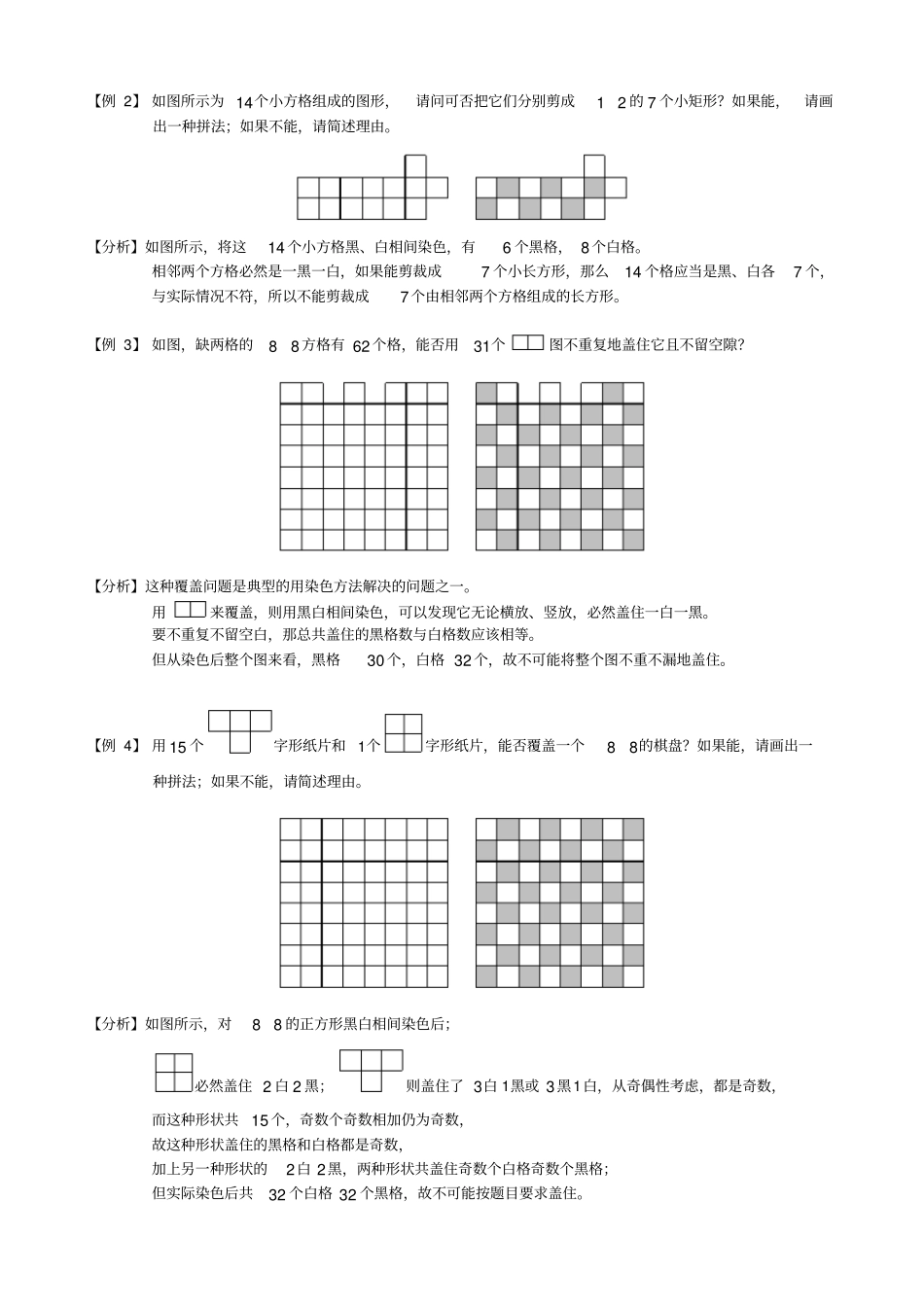
知识要点简单黑白相间染色【例1】如图是由40个小正方形组成的图形,能否将它剪裁成20个相同的长方形?如果能,请画出一种拼法;如果不能,请简述理由。【分析】将40个小正方形剪裁成20个相同的长方形,就是将图形分割成20个12的小长方形,将图形黑白相间染色后,发现有21黑,19白,黑、白格数目不等,而12的小长方形覆盖的总是黑白格各一个,所以不可能做到。这里的染色问题不是要求如何染色,然后问有多少种染色方法的那类题目,它指的是一种解题方法。染色方法是一种将题目研究对象分类的形象化方法,通过将问题中的对象适当染色,我们可以更形象地观察分析出其中所蕴含的关系,再经过一定的逻辑推理,便能得出问题的答案。这类问题不需要太多的数学知识,但技巧性、逻辑性较强,要注意学会几种典型的染色方法。最简单的染色问题是从一种民间游戏中发展起来的方格盘上的染色问题。解决这类问题的方法后来又发展成为解决方格盘铺盖问题的重要技巧。解决该类题目时,通常使用到数论,尤其是奇偶性等知识。染色与操作【例2】如图所示为14个小方格组成的图形,请问可否把它们分别剪成12的7个小矩形?如果能,请画出一种拼法;如果不能,请简述理由。【分析】如图所示,将这14个小方格黑、白相间染色,有6个黑格,8个白格。相邻两个方格必然是一黑一白,如果能剪裁成7个小长方形,那么14个格应当是黑、白各7个,与实际情况不符,所以不能剪裁成7个由相邻两个方格组成的长方形。【例3】如图,缺两格的88方格有62个格,能否用31个图不重复地盖住它且不留空隙?【分析】这种覆盖问题是典型的用染色方法解决的问题之一。用来覆盖,则用黑白相间染色,可以发现它无论横放、竖放,必然盖住一白一黑。要不重复不留空白,那总共盖住的黑格数与白格数应该相等。但从染色后整个图来看,黑格30个,白格32个,故不可能将整个图不重不漏地盖住。【例4】用15个字形纸片和1个字形纸片,能否覆盖一个88的棋盘?如果能,请画出一种拼法;如果不能,请简述理由。【分析】如图所示,对88的正方形黑白相间染色后;必然盖住2白2黑;则盖住了3白1黑或3黑1白,从奇偶性考虑,都是奇数,而这种形状共15个,奇数个奇数相加仍为奇数,故这种形状盖住的黑格和白格都是奇数,加上另一种形状的2白2黑,两种形状共盖住奇数个白格奇数个黑格;但实际染色后共32个白格32个黑格,故不可能按题目要求盖住。【例5】用11个和5个能否盖住88的大正方形?如果能,请画出一种拼法;如果不能,请简述理由。【分析】如图所示,对88的正方形黑白相间染色后;必然盖住2白2黑,5个则盖住10白10黑;则盖住了3白1黑或3黑1白,从奇偶性考虑,都是奇数;而这种形状共11个,奇数个奇数相加仍为奇数,故这种形状盖住的黑格和白格都是奇数,加上另一种形状的10白10黑,两种形状共盖住奇数个白格奇数个黑格;但实际染色后共32个白格32个黑格,故不可能按题目要求盖住。【例6】(2010年4月10日第十五届华罗庚金杯少年数学邀请赛小学组决赛A卷第9题)图1中有5个由4个11的小正方格组成的不同形状的硬纸板。问能用这5个硬纸板拼成图2中45的长方形吗?如果能,请画出一种拼法;如果不能,请简述理由。图1图2图3【分析】如图3所示,对45的正方形黑白相间染色后;、、、各盖住2白2黑,盖住3白1黑或3黑1白;这5个硬纸板共能盖住11白9黑或9黑11白;但实际染色后共10个白格10个黑格,故不可能按题目要求盖住。【例7】如图是半张中国象棋盘,棋盘上放有一只马。众所周知,马是走“日”字的。请问:这只马能否不重复地走遍这半张棋盘上的每一个点,然后回到出发点?馬馬【分析】马走“日”字,在中国象棋盘上走有什么规律呢?如图所示,先在棋盘各交点处相间标上○和●,图中共有22个○和23个●。因为马走“日”字,每步只能从○跳到●,或由●跳到○,所以马从某点跳到同色的点(指○或●),要跳偶数步;跳到不同色的点,要跳奇数步。现在马在○点,要跳回这一点,应跳偶数步,可是棋盘上共有232245个点,所以不可能做到不重复地走遍所有的点后回到出发点。【讨论】如果马的出发点不是在○点上而是在●点上,那么这只马能不能不重复地走遍这半张棋盘上...