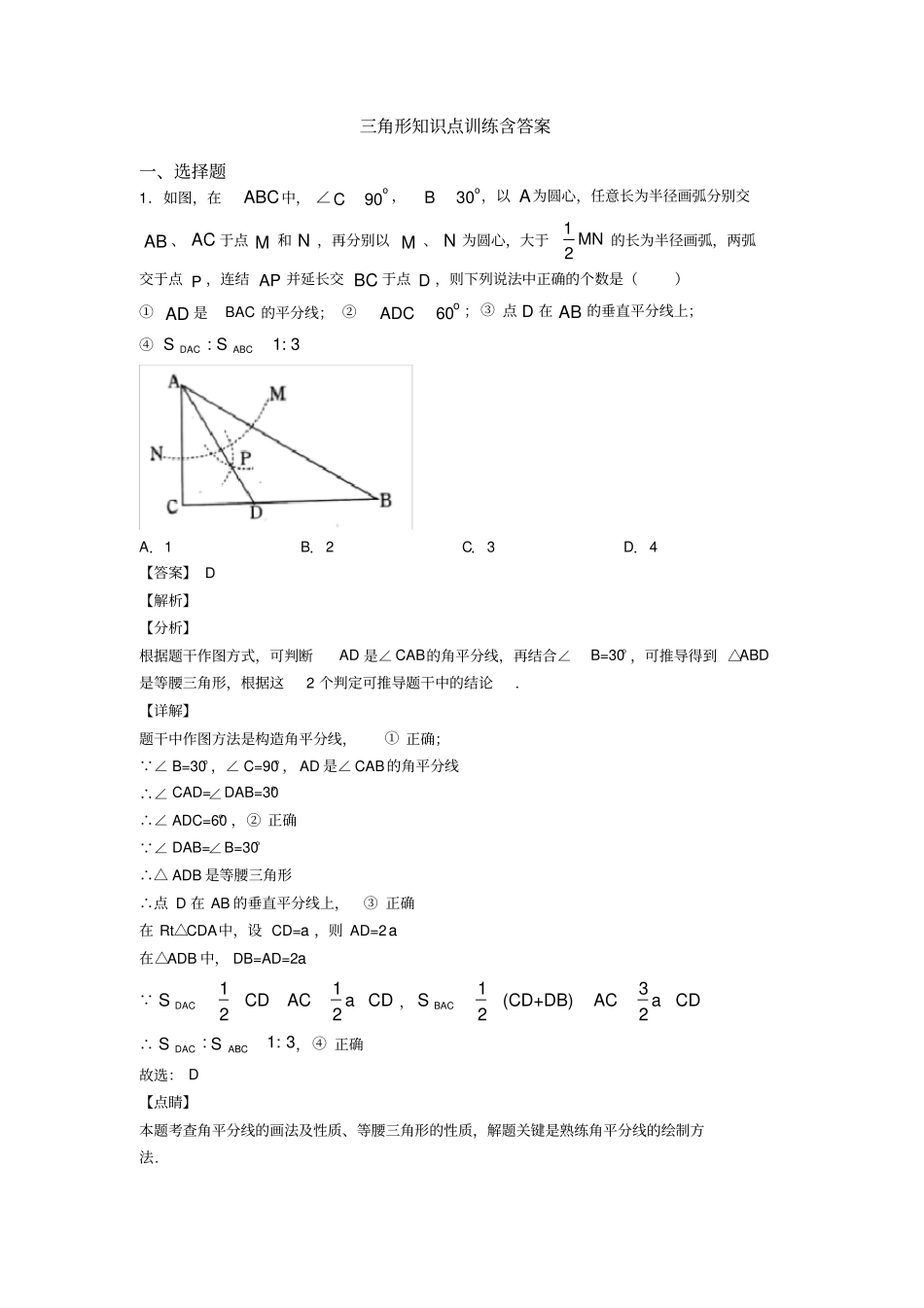
三角形知识点训练含答案一、选择题1.如图,在ABC中,90Co∠,30Bo,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于12MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是()①AD是BAC的平分线;②ADC60o;③点D在AB的垂直平分线上;④:1:3DACABCSSA.1B.2C.3D.4【答案】D【解析】【分析】根据题干作图方式,可判断AD是∠CAB的角平分线,再结合∠B=30°,可推导得到△ABD是等腰三角形,根据这2个判定可推导题干中的结论.【详解】题干中作图方法是构造角平分线,①正确; ∠B=30°,∠C=90°,AD是∠CAB的角平分线∴∠CAD=∠DAB=30°∴∠ADC=60°,②正确 ∠DAB=∠B=30°∴△ADB是等腰三角形∴点D在AB的垂直平分线上,③正确在Rt△CDA中,设CD=a,则AD=2a在△ADB中,DB=AD=2a 1122DACSCDACaCD,13(CD+DB)22BACSACaCD∴:1:3DACABCSS,④正确故选:D【点睛】本题考查角平分线的画法及性质、等腰三角形的性质,解题关键是熟练角平分线的绘制方法.2.如图,在矩形ABCD中,3,4,ABBC将其折叠使AB落在对角线AC上,得到折痕,AE那么BE的长度为()A.1B.2C.32D.85【答案】C【解析】【分析】由勾股定理求出AC的长度,由折叠的性质,AF=AB=3,则CF=2,设BE=EF=x,则CE=4x,利用勾股定理,即可求出x的值,得到BE的长度.【详解】解:在矩形ABCD中,3,4ABBC,∴∠B=90°,∴22345AC,由折叠的性质,得AF=AB=3,BE=EF,∴CF=5-3=2,在Rt△CEF中,设BE=EF=x,则CE=4x,由勾股定理,得:2222(4)xx,解得:32x;∴32BE.故选:C.【点睛】本题考查了矩形的折叠问题,矩形的性质,折叠的性质,以及勾股定理的应用,解题的关键是熟练掌握所学的性质,利用勾股定理正确求出BE的长度.3.如图,△ABC中,AB=AC=10,BC=12,D是BC的中点,DE⊥AB于点E,则DE的长为()A.65B.85C.125D.245【答案】D【解析】【分析】连接AD,根据已知等腰三角形的性质得出AD⊥BC和BD=6,根据勾股定理求出AD,根据三角形的面积公式求出即可.【详解】解:连接AD AB=AC,D为BC的中点,BC=12,∴AD⊥BC,BD=DC=6,在Rt△ADB中,由勾股定理得:AD=22221068ABBD, S△ADB=12×AD×BD=12×AB×DE,∴DE=8624105ADBDAB,故选D.【点睛】本题考查了等腰三角形的性质(等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合)、勾股定理和三角形的面积,能求出AD的长是解此题的关键.4.如图,ABCDY的对角线AC与BD相交于点O,ADBD,30ABD,若23AD.则OC的长为()A.3B.43C.21D.6【答案】C【解析】【分析】先根据勾股定理解RtABD△求得6BD,再根据平行四边形的性质求得3OD,然后根据勾股定理解RtAOD△、平行四边形的性质即可求得21OCOA.【详解】解: ADBD∴90ADB 在RtABD△中,30ABD,23AD∴243ABAD∴226BDABAD 四边形ABCD是平行四边形∴132OBODBD,12OAOCAC∴在RtAOD△中,23AD,3OD∴2221OAADOD∴21OCOA.故选:C【点睛】本题考查了含30°角的直角三角形的性质、勾股定理、平行四边形的性质等知识点,熟练掌握相关知识点是解决问题的关键.5.等腰三角形两边长分别是5cm和11cm,则这个三角形的周长为()A.16cmB.21cm或27cmC.21cmD.27cm【答案】D【解析】【分析】分两种情况讨论:当5是腰时或当11是腰时,利用三角形的三边关系进行分析求解即可.【详解】解:当5是腰时,则5+5<11,不能组成三角形,应舍去;当11是腰时,5+11>11,能组成三角形,则三角形的周长是5+11×2=27cm.故选D.【点睛】本题主要考查了等腰三角形的性质,三角形三边关系,掌握等腰三角形的性质,三角形三边关系是解题的关键.6.如图,在ABCV中,ABAC,30A,直线ab∥,顶点C在直线b上,直线a交AB于点D,交AC与点E,若1145,则2的度数是()A.30°B.35°C.40°D.45°【答案】C【解析】【分析】先根据等腰三角形的性质和三角形内角和可得ACB度数,由三角形外角的性质可得AED的度数,再根据平行线的性质得同位角相等,即可求得2.【详解】 ABAC,且30A,∴18030752ACB,在ADE中, 1145AAED,∴14514530115AEDA, //ab,∴2AEDACB,即21157540,故选:C.【...